А лгоритмы

Алгоритм - это последовательность точных и полных команд исполнителю совершить последовательность действий, направленных на достижение указанной цели или на решение поставленной задачи.

Алгоритм рассчитан на конкретного исполнителя (того, кто этот алгоритм будет исполнять). В качестве объекта-исполнителя может выступать как техническое устройство, так и живое существо. В информатике универсальным исполнителем алгоритмов является компьютер. Исполнителя характеризуют:

• среда (или обстановка) - "место обитания" исполнителя;

• система команд - каждый исполнитель может выполнять команды только из некоторого строго заданного списка.

• элементарные действия - то, что исполнитель совершает после вызова соответствующей команды;

• отказы - возникают, если команда вызывается при недопустимом для нее состоянии среды.

При автоматическом исполнении исполнитель выполняет все полученные команды, не задавая никаких вопросов.

Свойства алгоритмов:

1. Дискретность - алгоритм должен состоять из конкретных действий, следующих в определенном порядке;

2. Понятность - алгоритм должен содержать указания, которые понятны исполнителю.

3. Конечность - решение достигается за конечное число шагов или делается вывод о невозможности продолжения алгоритма;

4. Массовость - алгоритм должен быть применен для целого класса подобных задач.

5. Однозначность - единственность толкования правил выполнения действий и порядка их выполнения.

Основные алгоритмические структуры:

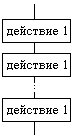
1. Линейные алгоритмы - все действия выполняются последовательно.

2. Разветвляющиеся алгоритмы - выполнение действий зависит от условий.

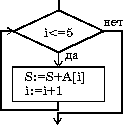
3. Циклические алгоритмы - действия повторяются многократно.

Я зыки программирования

Язык программирования – это средство для создания новых программ.

Реализация основных алгоритмических структур на языке программирования Бейсик.

Линейные	Ветвления	Цикл «Для каждого»
PRINT Сообщить LET Присвоить INPUT Запросить	IF Q THEN D1 ELSE D2 Если Q то D1 иначе D2	FOR I=A TO B D NEXT I Для I от A до B D Конец цикла по I

Массив - это множество однотипных элементов, объединённых общим именем и занимающих в компьютере определённую область памяти. Например, список фамилий

учеников вашей группы — массив, численные данные о среднесуточной температуре за месяц — массив. Кроме термина массив иногда употребляют понятия таблица или матрица.

Различают одномерные и двумерные массивы. Одномерные массивы состоят из одной

строки, а двумерные - из нескольких строк и столбцов.

DIM A(N) - описать массив - это значит предоставить N свободных ячеек в памяти ЭВМ для массива с именем А; DIM В(М,N) - описание двумерного массива.

Операция поиска в массиве сводится к нахождению элемента по заданным условиям.

Например, Пример 6: Вывести минимальный и максимальный элементы массива, состоящего из 10 целых чисел.

CLS DIM a(10) FOR i = 1 TO 10 INPUT A(i) NEXT i m = a(1) n = a(1)

FOR z = 1 TO 10 IF a(z) > m THEN m = a(z) NEXT z FOR j = 1 TO 10 IF a(j) < n THEN n = a(j) NEXT j PRINT "max", m PRINT "min", n

А рифметические и логические основы работы компьютера.

Логика – это наука о формах и законах человеческого мышления и, в частности, о законах доказательных рассуждений. Ее основателем считается величайший древнегреческий философ Аристотель.

Высказывание - это повествовательное предложение, относительно которого можно сказать, истинно оно или ложно. Обозначать высказывание будем латинскими прописными буквами. Например: А = Число 12345 кратно 3.

Если высказывание А истинное, то будем писать "А=1" и говорить "А - истинно".

Если высказывание А ложное, то будем писать "А=0" и говорить "А - ложно".

Из простых высказываний можно получить сложное высказывание, объединив с помощью логических операций. Сложное высказывание также является истинным или ложным, но это значение вычисляется в соответствии с таблицами истинности входящих в него логических операций.

Логические операции	Таблица истинности
Логическое отрицание (инверсия) образуется из высказывания с помощью добавления частицы "не" к высказыванию	В ывод: инверсия высказывания истинна, когда высказывание ложно, и ложна, когда высказывание истинно.
Логическое сложение (дизъюнкция) образуется соединением двух высказываний в одно с помощью союза "или".	В ывод: дизъюнкция двух высказываний ложна тогда и только тогда, когда оба высказывания ложны, и истинна, когда хотя бы одно высказывание истинно.
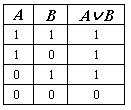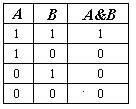Логическое умножение (конъюнкция) образуется соединением двух высказываний в одно с помощью союза "и".	В ывод: конъюнкция двух высказываний истинна тогда и только тогда, когда оба высказывания истинны, и ложна, когда хотя бы одно высказывание ложно.