Призмою, описаною навколо циліндра, називається призма, у якої площинами основ є площини основ циліндра, а бічні грані дотикаються до циліндра (мал. 8).

5. Конус

Конусом (точніше, круговим конусом) називається тіло, яке складається з круга — основи конуса, точки, яка не лежить у площині цього круга — вершини конуса і всіх відрізків, що сполучають вершину конуса з точками основи (мал. 9). Відрізки, що сполучають вершину конуса з точками кола основи, називаються твірними конуса. Поверхня конуса складається з основи і бічної поверхні.

Мал.9 Мал.10

Конус називається прямим, якщо пряма, що сполучає вершину конуса з центром основи, перпендикулярна до

площини основи. Далі розглядатимемо лише прямий конус, називаючи його просто конусом. Наочно прямий круговий конус можна розглядати як ті­ло, утворене в результаті обертання прямокутного трикутника навколо його катета як осі (мал. 10).

Висотою конуса називається перпендикуляр, опущений з його вершини на площину основи. У прямого конуса основа висоти збігається з центром основи. Віссю прямого кругового конуса називається пряма, яка містить його висоту.

6. Перерізи конуса площинами

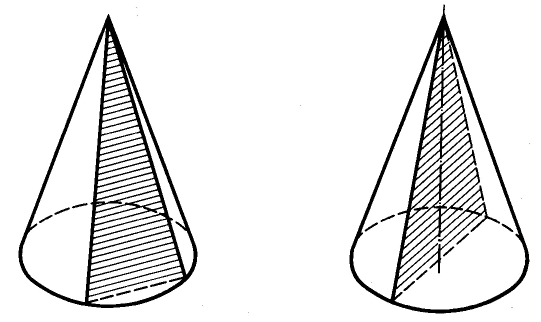
Переріз конуса площиною, яка проходить через його верши­ну, є рівнобедрений трикутник, у якого бічні сторони е твірними конуса (мал. 11). Зокрема, рівнобедреним трикутником е осьо­вий переріз конуса. Це переріз, який проходить через вісь конуса (мал. 12).

Теорема: Площина, паралельна площині основи конуса, перетинає конус по кругу, а бічну поверхню — по колу з центром на осі конуса.

Доведення. Нехай — площина, яка

Мал. 11 Мал.12 Мал.13 паралельна пло­щині основи конуса і перетинає конус (мал. 13). Перетворення гомотетії відносно вершини конуса, яке суміщає площину з площиною основи, суміщає переріз конуса площиною з осно­вою конуса. Отже, переріз конуса площиною є круг, а переріз бічної поверхні – коло з центром на осі конуса. Теорему доведено.

Площина, яка паралельна основі конуса і перетинає конус, відтинає від нього менший конус. Частина, що залишилася, називається зрізаним конусом.

7. Вписана і описана піраміди

Пірамідою, вписаною в конус, називається така піраміда, основою якої є многокутник, вписаний у коло основи конуса, а вершиною — вершина конуса (мал. 14). Бічні ребра піраміди, вписаної в конус, є твірними конуса.

Дотичною площиною до конуса називається площина, яка проходить через твірну конуса і перпендикулярна до площини осьового перерізу, проведеного через цю твірну (мал. 15).

Пірамідою, описаною навколо конуса, називається піраміда, в основі якої лежить многокутник, описаний навколо основи конуса, а вершина збігається з вершиною конуса (мал. 16). Площини бічних граней описаної піраміди є дотичними площи­нами до конуса.

Мал. 14 Мал.15 Мал.16 Мал.17

Питання для самоконтролю:

1. Дайте визначення циліндра.

2. Який циліндр називається прямим?

3. Що таке радіус циліндра, висота циліндра, вісь циліндра, осьовий переріз циліндра?

4. Що таке призма, вписана у циліндр(описана навколо циліндра)?

5. Що таке круговий конус, вершина конуса, твірна конуса, основа конуса, бічна поверхня конуса?

6. Який конус називається прямим?

7. Що таке висота конуса, вісь конуса, осьовий переріз конуса?

8. Що таке зрізаний конус?

9. Яка піраміда називається вписаною у конус (описаною навколо конуса)?

10. Чому дорівнює площа бічної поверхні циліндра?

11. Чому дорівнює площа бічної поверхні конуса?

12. Чому дорівнює об’єм циліндра?

13. Чому дорівнює об’єм конуса?

Циліндр

	Площа бічної поверхні циліндра обчислюється за формулою: де R – радіус, а H – висота циліндра. Об'єм циліндра дорівнює добутку площі його основи на висоту:
	Твірні - відрізки, що з'єднують вершину з точками основи. Висота - перпендикуляр, проведений з вершини до центра основи. Площа бічної поверхні конуса дорівнює половині добутку довжини кола основи на твірну: , де l - твірна. Об'єм конуса дорівнює одній третій добутку площі його основи на висоту: Площа зрізаного конуса дорівнює: Об'єм зрізаного конуса дорівнює: