
- •Рекомендовано к печати редакционно-издательским советом
- •1. Решение рациональных уравнений. Краткие теоретические сведения
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Задания для решения
- •Домашнее задание
- •13. Векторная алгебра Краткие теоретические сведения
- •Решение типовых задач
- •Задания для решения
- •Домашнее задание
- •14. Прямая на плоскости Краткие теоретические сведения
- •Решение типовых задач
- •Задания для решения
- •Домашнее задание
- •15. Определители Краткие теоретические сведения
- •Решение типовых задач
- •Решение типовых задач
- •Ответ. . Задания для решения
- •Домашнее задание
- •17. Матричная алгебра Краткие теоретические сведения
- •Решение типовых задач
- •Задания для решения
- •Решение типовых задач
- •Решение типовых задач
- •Задания для решения
- •Домашнее задание
- •20. Однородные системы уравнений. Фундаментальный набор решений Краткие теоретические сведения
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Задания для решения
- •Решение типовых задач
- •Задания для решения
- •Домашнее задание
- •25. Задачи на наибольшее и наименьшее значения функции Краткие теоретические сведения
- •Решение типовых задач
- •Решение типовых задач
- •Задания для решения
- •Домашнее задание
- •28. Интегрирование иррациональных выражений Краткие теоретические сведения
- •29. Интегрирование тригонометрических выражений
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Задания для решения
- •Решение типовых задач
Решение типовых задач
Пример
1. Решите
систему уравнений
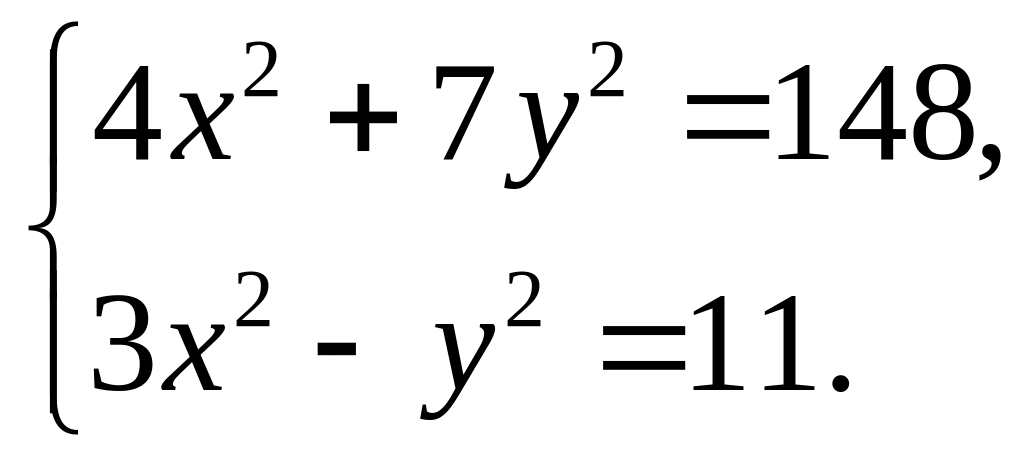
Решение.
Решим данную систему уравнений методом
подстановки. Из второго уравнения
находим:
![]() .
Подставляя это значение в первое
уравнение, получаем:
.
Подставляя это значение в первое
уравнение, получаем:
![]() или после упрощения
или после упрощения
![]() .
Корнями этого уравнения являются числа
.
Корнями этого уравнения являются числа
![]() ,
,
![]() .
Таким образом, получаем совокупность
двух систем уравнений:
.
Таким образом, получаем совокупность
двух систем уравнений:
![]() и
и
![]() .
.
Первая
система имеет решения
![]() ,
а вторая
,
а вторая
![]() .
Значит, данная система имеет решения:
.
Значит, данная система имеет решения:
![]() .
.
Ответ. .
Пример
2.
Решите
систему уравнений

Решение.
Метод подстановки в данном случае
приводит к сложным выкладкам. Поэтому
будем рассуждать иначе: прибавим к
первому уравнению системы второе
уравнение, тогда получаем систему:

 равносильную заданной.
равносильную заданной.
А теперь воспользуемся методом подстановки:
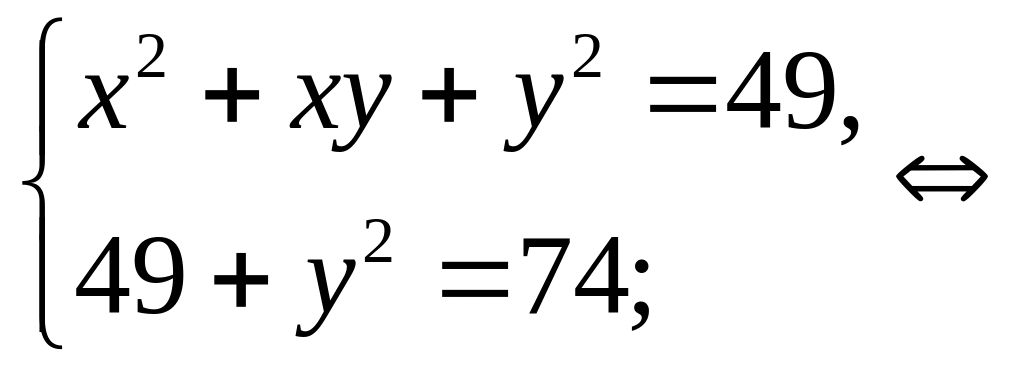
![]() .
.
Полученная система уравнений равносильна совокупности двух систем уравнений:
 ,
,
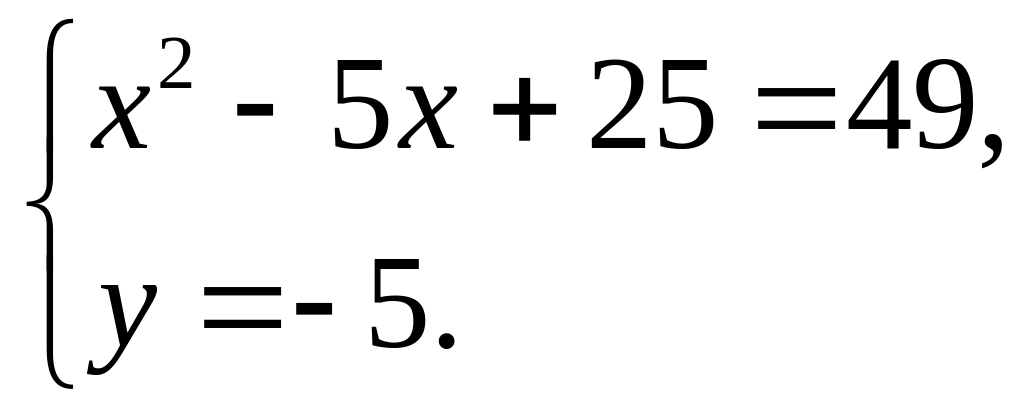
Первая
система имеет решение
![]() ,
а вторая
,
а вторая
![]() .
Значит, решение данной системы имеет
вид:
.
Значит, решение данной системы имеет
вид:
![]() .
.
Ответ. .
Пример
3. Решите
систему
![]()
Решение.
Обозначим выражение
![]() переменной
переменной
![]() ,
тогда получим новую систему уравнений
,
тогда получим новую систему уравнений
![]()
Решая первое уравнение системы, получаем:
![]()
![]() D0;
D0;
![]()
![]()
Перейдем
к переменным
и
![]() ,
и решим соответствующие совокупности
систем уравнений.
,
и решим соответствующие совокупности
систем уравнений.
Если
![]() то
система примет вид:
то
система примет вид:
![]() ;
тогда
;
тогда
![]() ,
откуда
,
откуда
![]() и
и
![]()
Если
![]() то
система примет вид:
то
система примет вид:
![]() ;
тогда
;
тогда
![]() ,
откуда
,
откуда
![]() и
и
![]()
Данная система имеет четыре решения:
(1;1), (0,5;2), (2;-1), (-0,5;4).
Ответ. (1;1), (0,5;2), (2;-1), (-0,5;4).
Пример
4. Решите
систему уравнений:
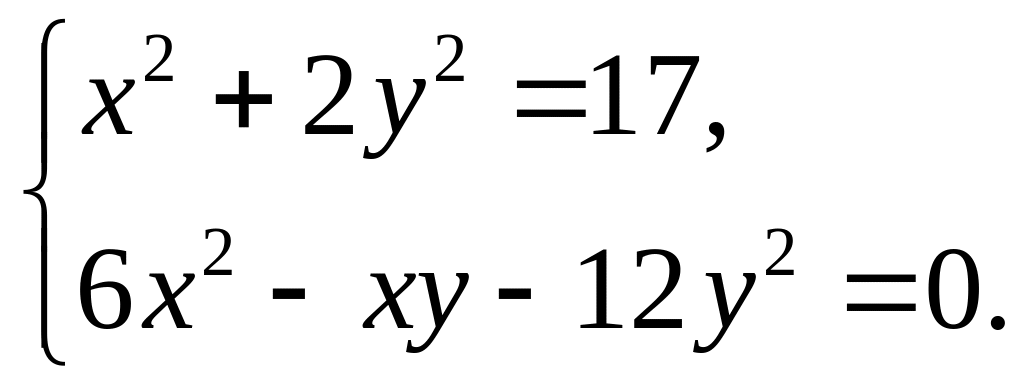
Решение.
Второе уравнение системы представим в
виде:
![]() .
Тогда данная система будет равносильна
совокупности двух систем, решаемых
методом подстановки.
.
Тогда данная система будет равносильна
совокупности двух систем, решаемых
методом подстановки.
1.
 или
или
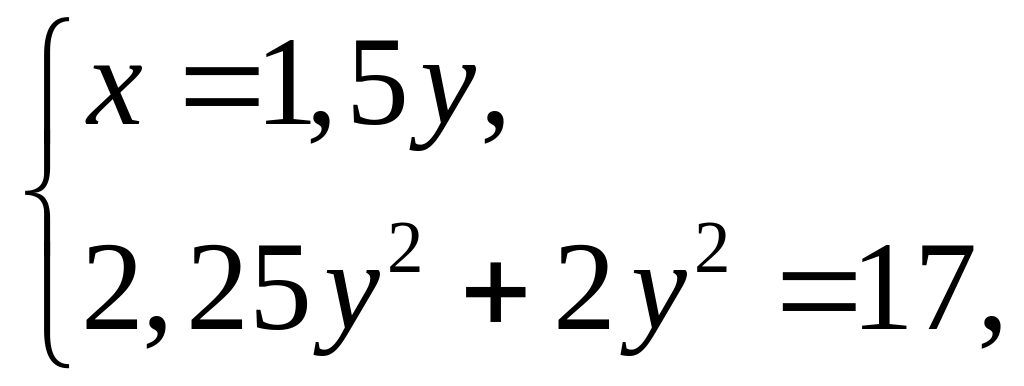 ,
значит,
,
значит,
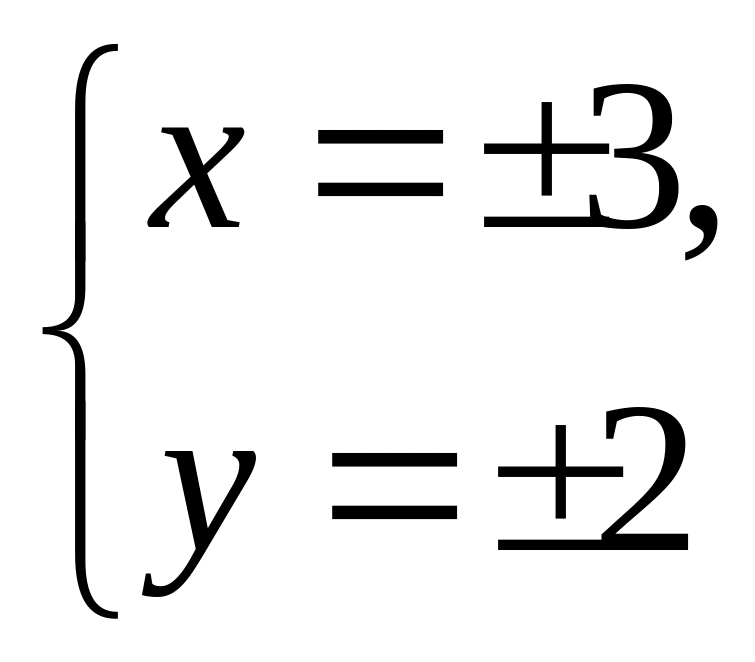 и решением первой системы будет
и решением первой системы будет
![]() .
.
2.![]() или
или
![]()
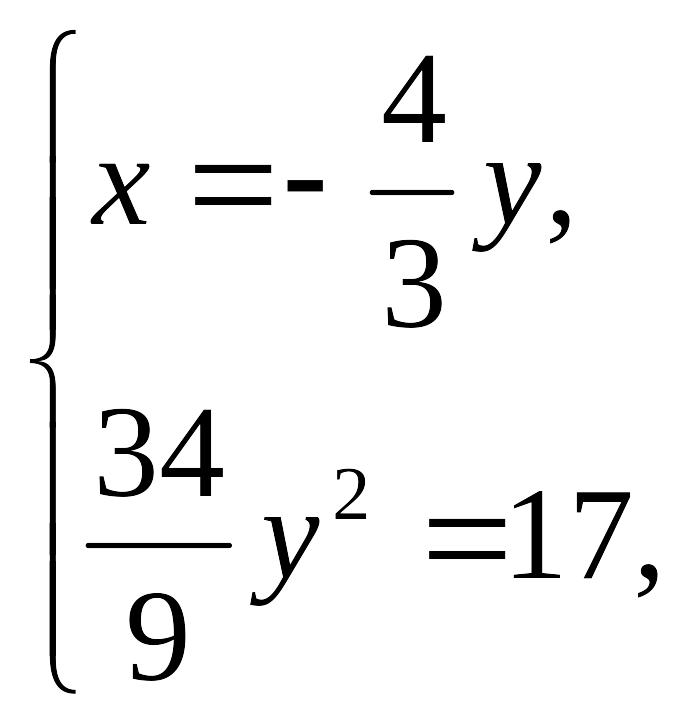 ,
значит
,
значит
![]() ,
и решением второй системы будет
,
и решением второй системы будет
![]() .
.
Ответ. и .
Задания для решения
Решить системы уравнений.
2.1.
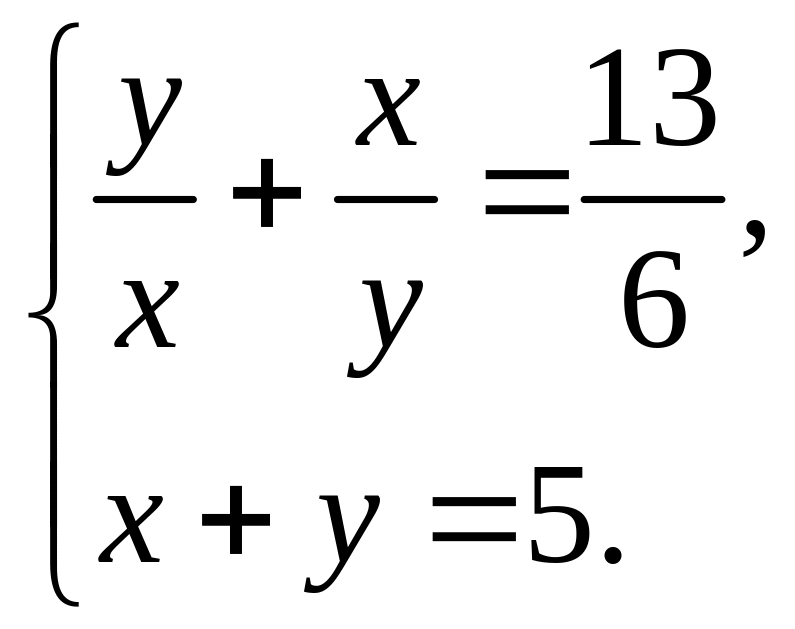 2.2.
2.2.
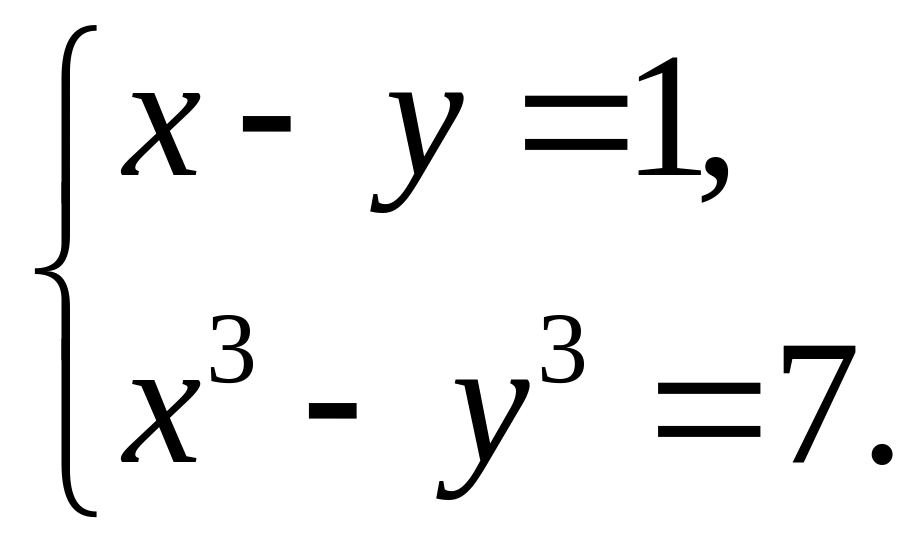
2.3.
 2.4.
2.4.
![]()
2.5.
![]() 2.6.
2.6.
![]()
2.7.
![]() 2.8.
2.8.
![]()
2.9.
![]() 2.10.
2.10.
![]()
2.11.
![]() 2.12.
2.12.
![]()
Домашнее задание
Решить системы уравнений.
2.13.
![]() 2.14.
2.14.
![]()
2.15.
![]() 2.16.
2.16.
![]()
2.17.
![]() 2.18.
2.18.
![]()
Ответы
2.1
(2;3), (3;2). 2.2
(2;1), (-1;-2). 2.3
(0,4;0,8). 2.4
(2;3), (3;2).
2.5
(4;1), (1;4). 2.6
(1;2). 2.7
(0,5;4). 2.8
(7;3), (-7;-3). 2.9
(2;-1), (-1;2).
2.10
(2;1), (2;-1),
(1;![]() ),
(1;
),
(1;![]() ).
2.11
(1;2), (2;1). 2.12
).
2.11
(1;2), (2;1). 2.12
![]() ,
,
![]() .
2.13
(-3;1), (1;-3). 2.14
(-2;-1), (1;2). 2.15
(1;2). 2.16
(-2;-1), (-2;1), (2;-1), (2;1). 2.17
(4;2). 2.18 (-3;-2),
(3;1).
.
2.13
(-3;1), (1;-3). 2.14
(-2;-1), (1;2). 2.15
(1;2). 2.16
(-2;-1), (-2;1), (2;-1), (2;1). 2.17
(4;2). 2.18 (-3;-2),
(3;1).
3. Уравнения и неравенства с модулем
Краткие теоретические сведения
При решении уравнений, содержащих переменную под знаком модуля, применяются чаще всего следующие методы:
1) раскрытие модуля по определению;
2) возведение обеих частей уравнения в квадрат;
3) метод разбиения на промежутки.
При решении неравенства, содержащих переменную под знаком модуля, иногда бывает полезна теорема 1 о равносильности неравенств.
Теорема
1. Пусть дано
неравенство
![]() причем
причем
![]() и
и
![]() при всех
при всех
![]() из
области определения неравенства. Если
обе части возвести в одну и туже
натуральную степень
из
области определения неравенства. Если
обе части возвести в одну и туже
натуральную степень
![]() и
при этом знак неравенства оставить без
изменения, то получится неравенство
и
при этом знак неравенства оставить без
изменения, то получится неравенство
![]() равносильное данному.
равносильное данному.
Пусть,
например, нужно решить неравенство
![]() Воспользуемся тем, что если
Воспользуемся тем, что если
![]() - некоторая функция, то
- некоторая функция, то
![]() и
и
![]()
Это
значит. что по теореме 1 неравенство
![]() равносильно неравенству
равносильно неравенству
![]() Кроме того, иногда полезно воспользоваться
геометрической интерпретацией модуля
действительного числа. Дело в том, что
геометрически
Кроме того, иногда полезно воспользоваться
геометрической интерпретацией модуля
действительного числа. Дело в том, что
геометрически
![]() означает расстояние от точки
означает расстояние от точки
![]() числовой
координат, а
числовой
координат, а
![]() расстояние между точками
расстояние между точками
![]() и
и
![]()
