
- •Рекомендовано к печати редакционно-издательским советом
- •1. Решение рациональных уравнений. Краткие теоретические сведения
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Задания для решения
- •Домашнее задание
- •13. Векторная алгебра Краткие теоретические сведения
- •Решение типовых задач
- •Задания для решения
- •Домашнее задание
- •14. Прямая на плоскости Краткие теоретические сведения
- •Решение типовых задач
- •Задания для решения
- •Домашнее задание
- •15. Определители Краткие теоретические сведения
- •Решение типовых задач
- •Решение типовых задач
- •Ответ. . Задания для решения
- •Домашнее задание
- •17. Матричная алгебра Краткие теоретические сведения
- •Решение типовых задач
- •Задания для решения
- •Решение типовых задач
- •Решение типовых задач
- •Задания для решения
- •Домашнее задание
- •20. Однородные системы уравнений. Фундаментальный набор решений Краткие теоретические сведения
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Задания для решения
- •Решение типовых задач
- •Задания для решения
- •Домашнее задание
- •25. Задачи на наибольшее и наименьшее значения функции Краткие теоретические сведения
- •Решение типовых задач
- •Решение типовых задач
- •Задания для решения
- •Домашнее задание
- •28. Интегрирование иррациональных выражений Краткие теоретические сведения
- •29. Интегрирование тригонометрических выражений
- •Решение типовых задач
- •Решение типовых задач
- •Решение типовых задач
- •Задания для решения
- •Решение типовых задач
Решение типовых задач
Пример
1. Доказать,
что система векторов
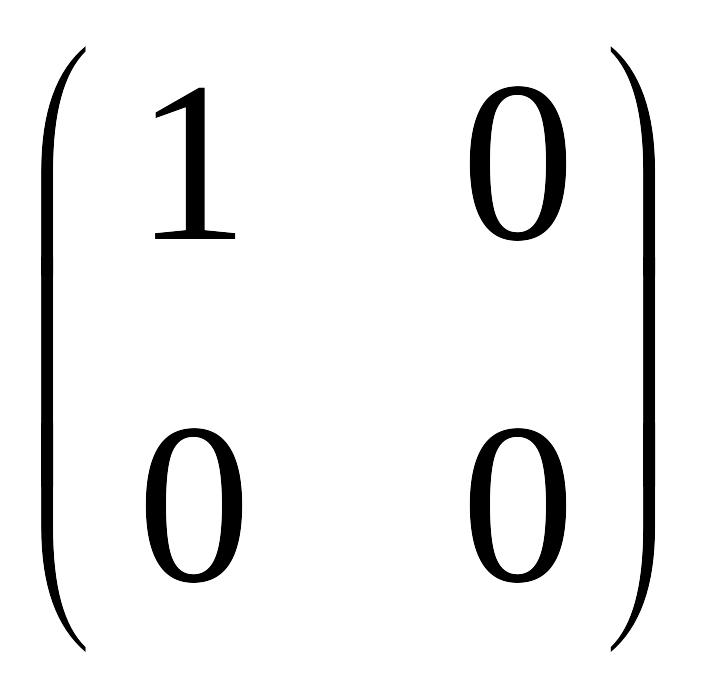 ,
,
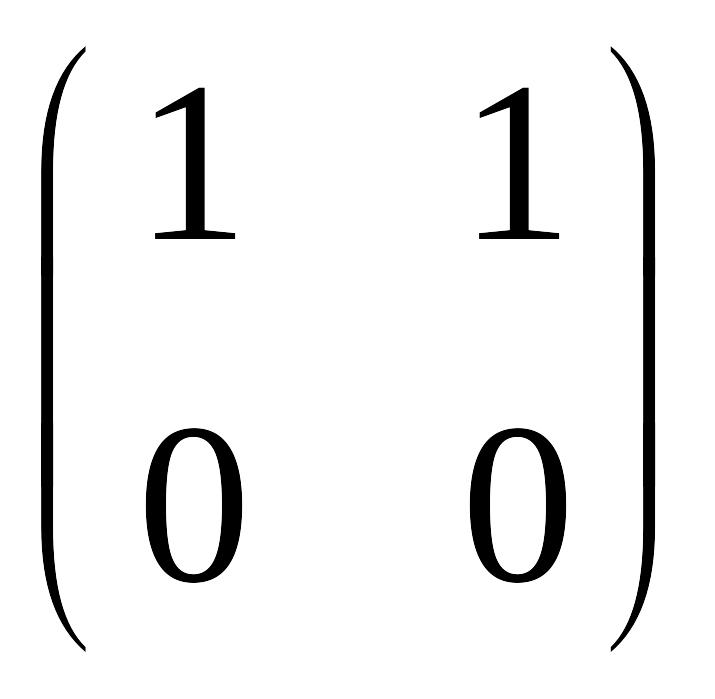 ,
,
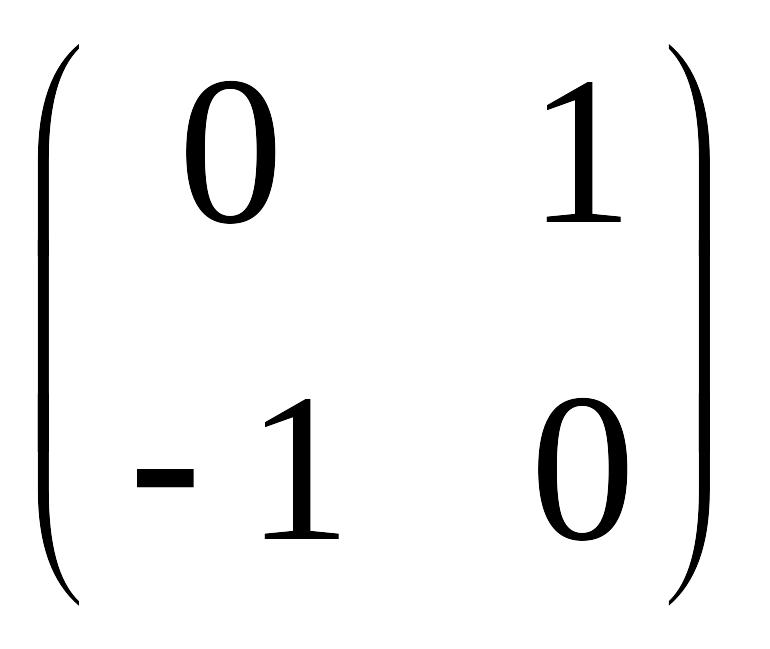
линейного пространства квадратных матриц второго порядка с действительными элементами линейно независима.
Решение.
Найдём
значения ![]() ,
при которых выполняется равенство
,
при которых выполняется равенство
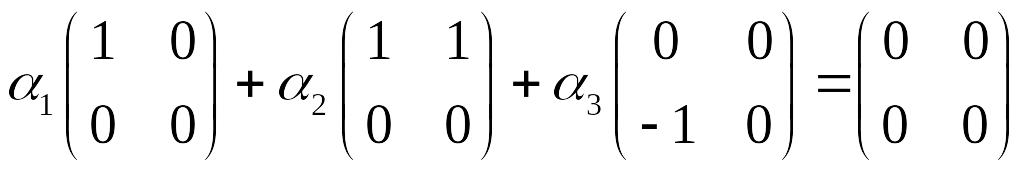 ,
,
или
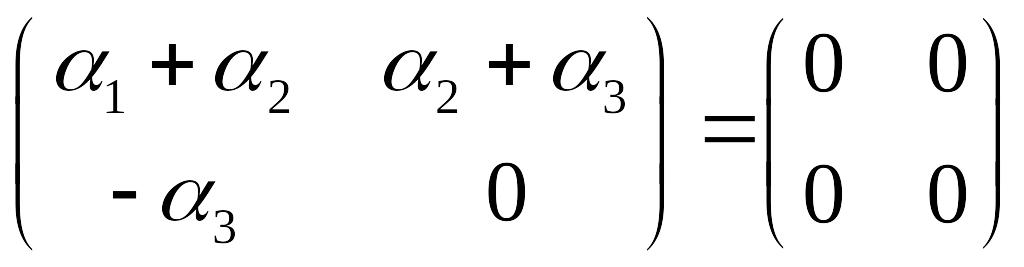
Это равенство равносильно системе уравнений
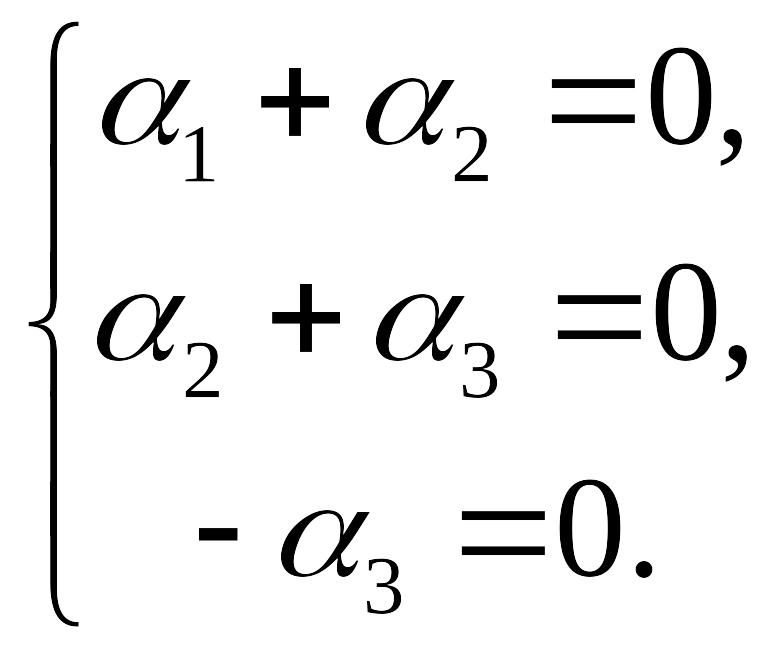
Полученная система уравнений имеет только нулевое решение
![]() .
Следовательно, система векторов линейна
независима.
.
Следовательно, система векторов линейна
независима.
Пример
2. Векторы
![]() ,
,
![]() ,
,
![]() и
и
![]() заданы своими координатами в некотором
базисе. Показать, что векторы
заданы своими координатами в некотором
базисе. Показать, что векторы
![]() сами
образуют базис, и найти координаты
вектора
в
этом базисе.
сами
образуют базис, и найти координаты
вектора
в
этом базисе.
Решение. Так как каждый из данных векторов имеет три координаты, то эти векторы принадлежат трёхмерному пространству. Для того чтобы три вектора составляли базис трёхмерного пространства достаточно, чтобы они были линейно независимыми. Составим матрицу , столбцы которой есть координаты векторов , и найдём её ранг:
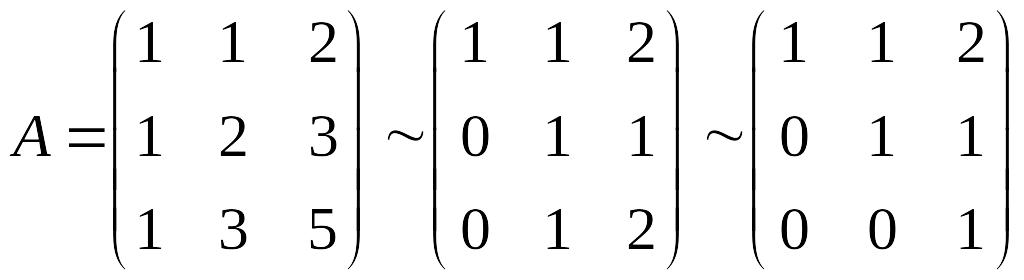
Ранг матрицы равен 3, следовательно, векторы линейно независимы и, значит, составляют базис пространства.
Для
нахождения координат
вектора
составим и
решим векторное уравнение
![]() , или
, или
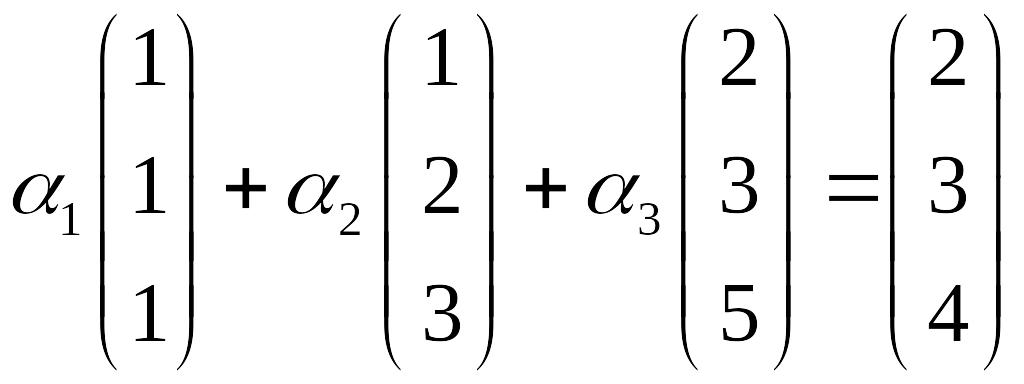 .
.
Это уравнение равносильно системе линейных уравнений с такой расширенной матрицей
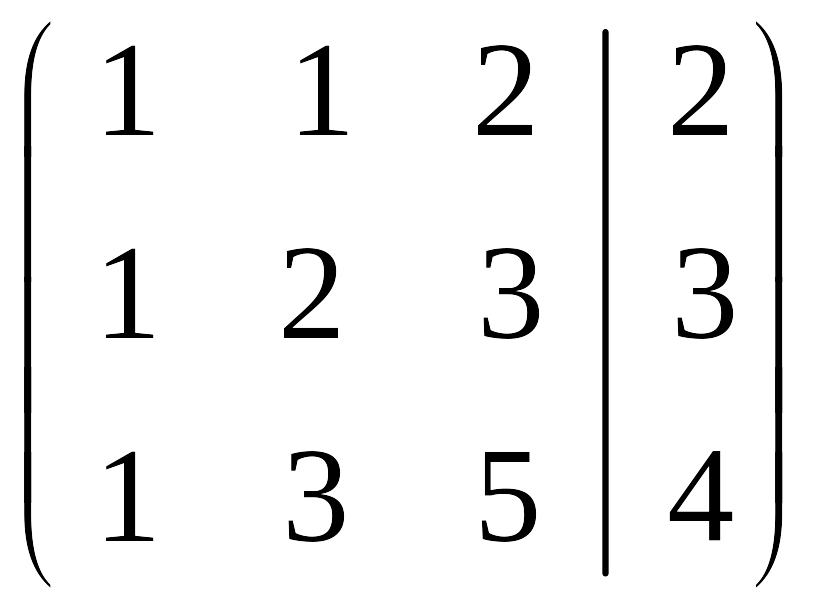 .
.
Используя
метод Гаусса, получим ![]() .
.
Задания для решения
19.1.
Проверить,
что векторы ![]() образуют базис трехмерного пространства;
найти координаты вектора
в этом базисе:
образуют базис трехмерного пространства;
найти координаты вектора
в этом базисе:
а)
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
б)
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
19.2.
Доказать,
что матрицы
![]() образуют базис пространства квадратных
матриц второго порядка с действительными
элементами, и найти координаты матрицы
в этом базисе.
образуют базис пространства квадратных
матриц второго порядка с действительными
элементами, и найти координаты матрицы
в этом базисе.
а)
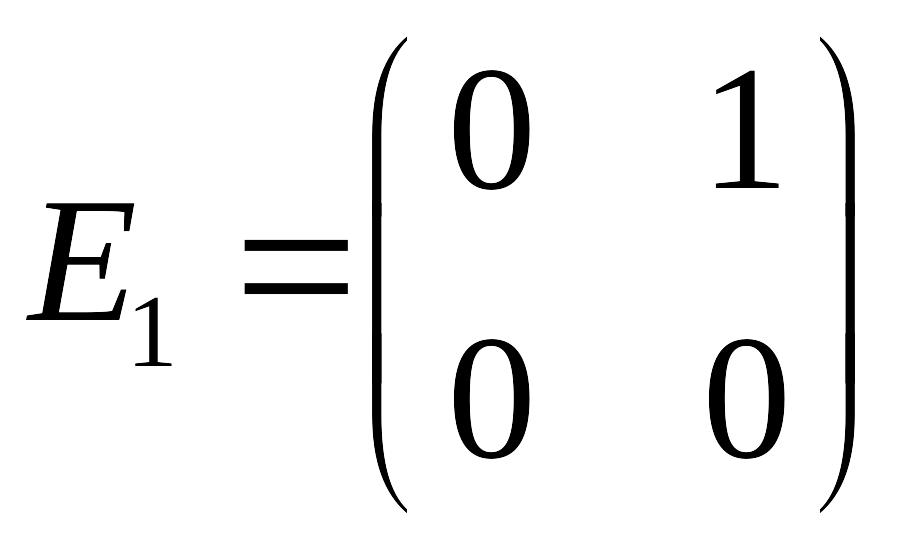 ,
,
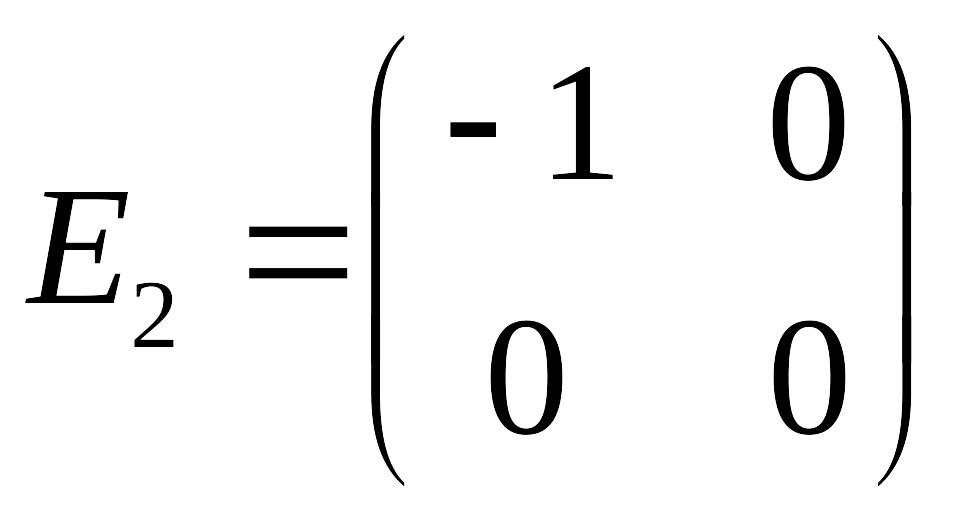 ,
,
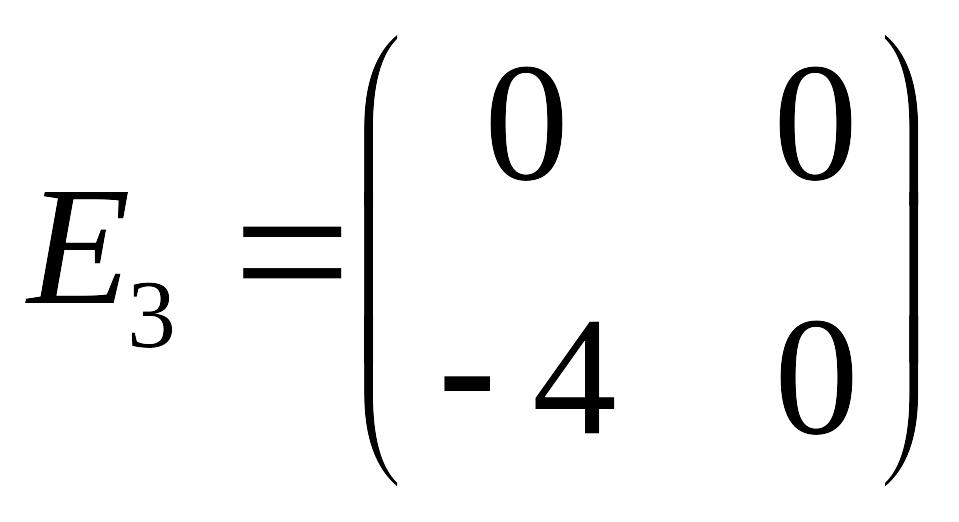 ,
,
 ;
;
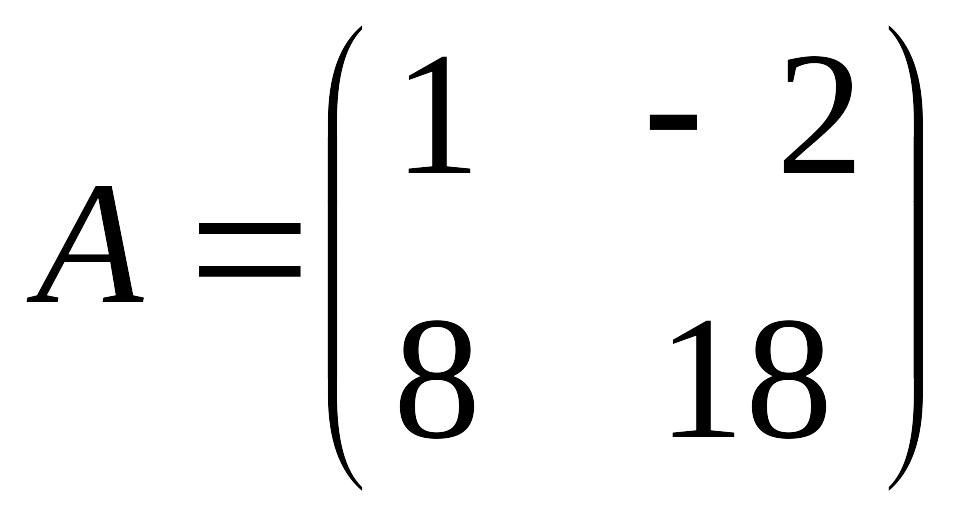 .
.
б)
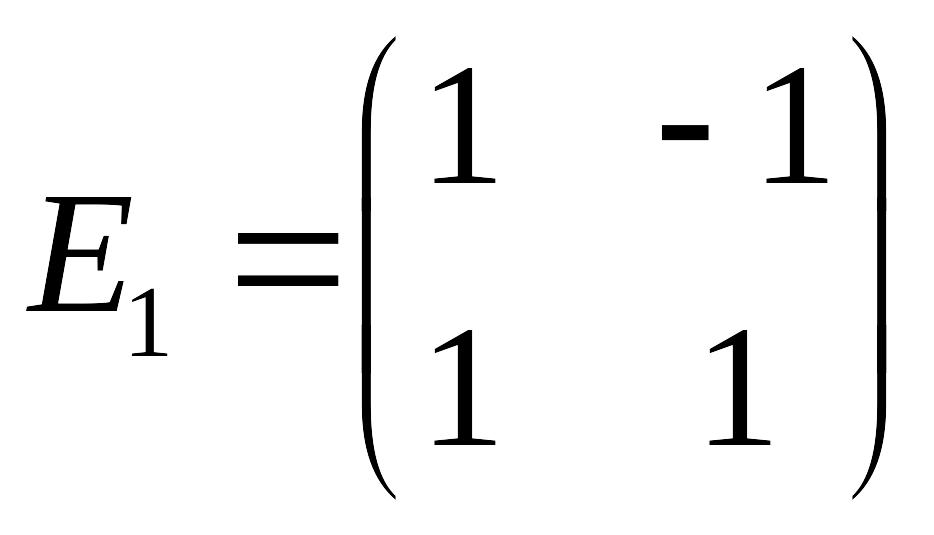 ,
,
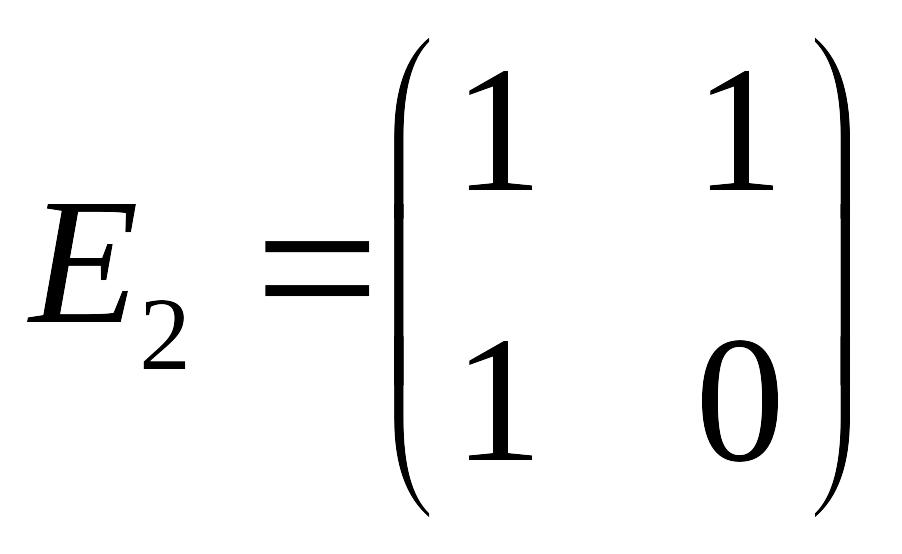 ,
,
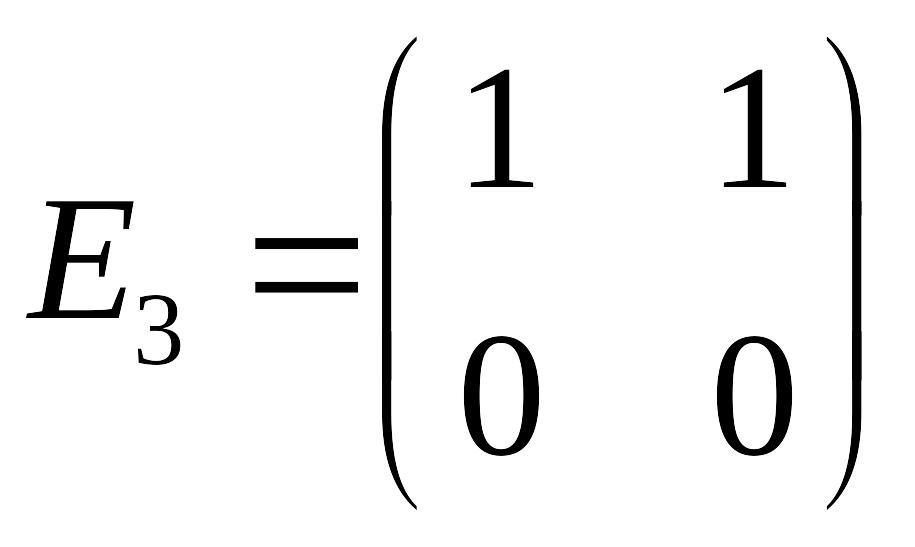 ,
,
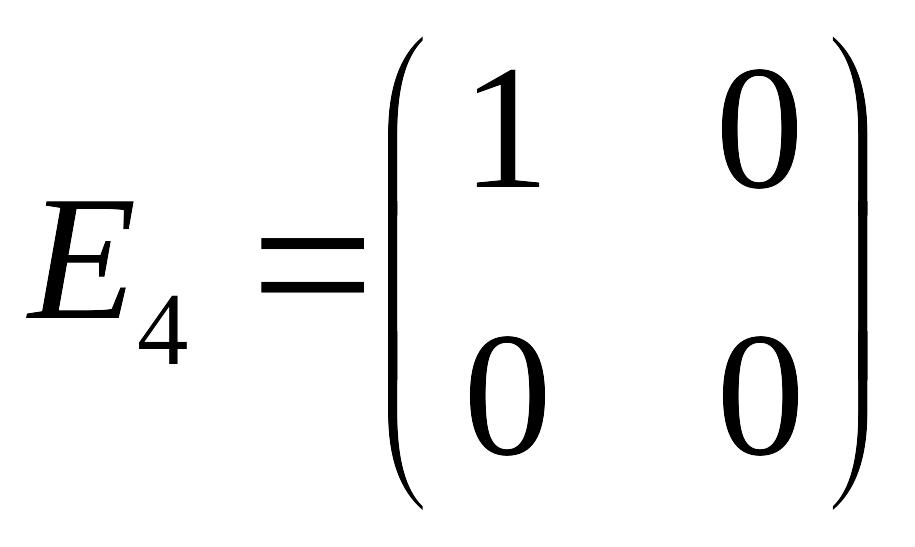 ;
;
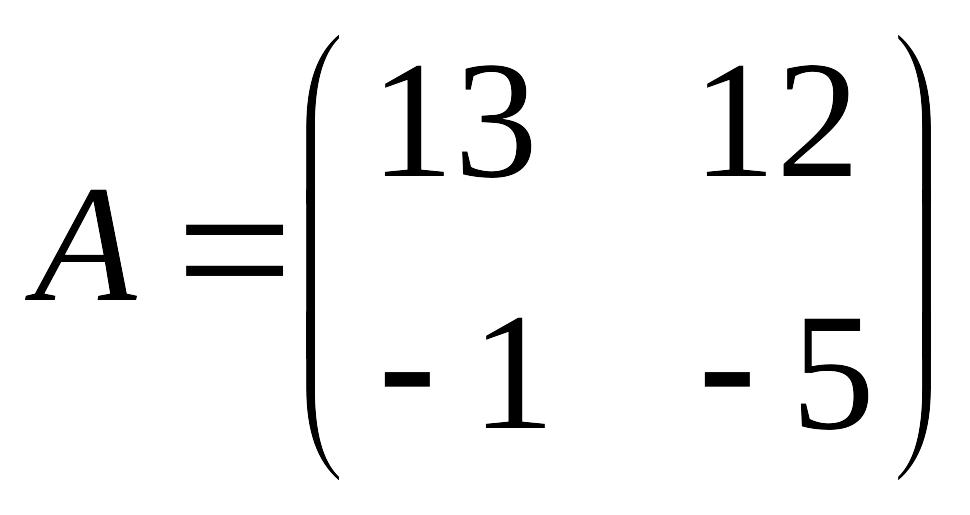 .
.
19.3.
Исследовать на линейную зависимость
систему векторов
![]() ,
,
![]() ,
,
![]() .
.
19.4.
Доказать, что векторы
![]() образуют базис векторного пространства
образуют базис векторного пространства
![]() .
Разложить вектор
.
Разложить вектор
![]() по этому базису, если
по этому базису, если
![]() .
.
Домашнее задание
19.5.
Доказать, что система векторов линейно
зависима
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
19.6.
Доказать,
что векторы
![]()
![]() образуют базис в
(если известно, что размерность
равна четырем) и разложить вектор
образуют базис в
(если известно, что размерность
равна четырем) и разложить вектор
![]() по этому базису.
по этому базису.
Ответы
19.1.
а)
![]() ,
б) (0, 5,
4). 19.2.
а) (-2,
-1,
-2,
6),
б) (-5,
4, 3, 11). 19.3.
система линейно зависима. 19.4.
,
б) (0, 5,
4). 19.2.
а) (-2,
-1,
-2,
6),
б) (-5,
4, 3, 11). 19.3.
система линейно зависима. 19.4.
![]() .
19.6.
.
19.6.
![]()
20. Однородные системы уравнений. Фундаментальный набор решений Краткие теоретические сведения
Рассмотрим однородную линейную систему
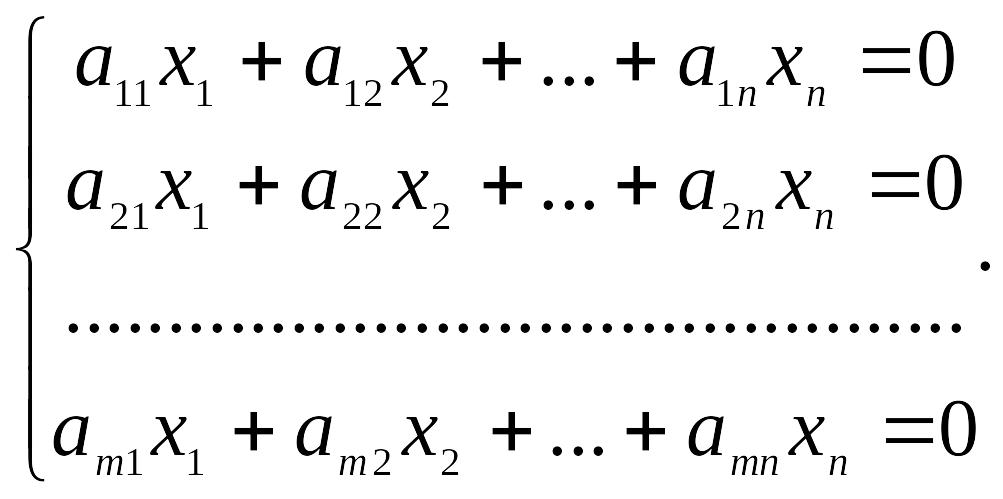 (1.20)
(1.20)
Очевидно,
что такая система всегда совместна,
поскольку имеет нулевое решение
![]() называемое тривиальным.
называемое тривиальным.
Матрицей системы (6) называется матрица вида
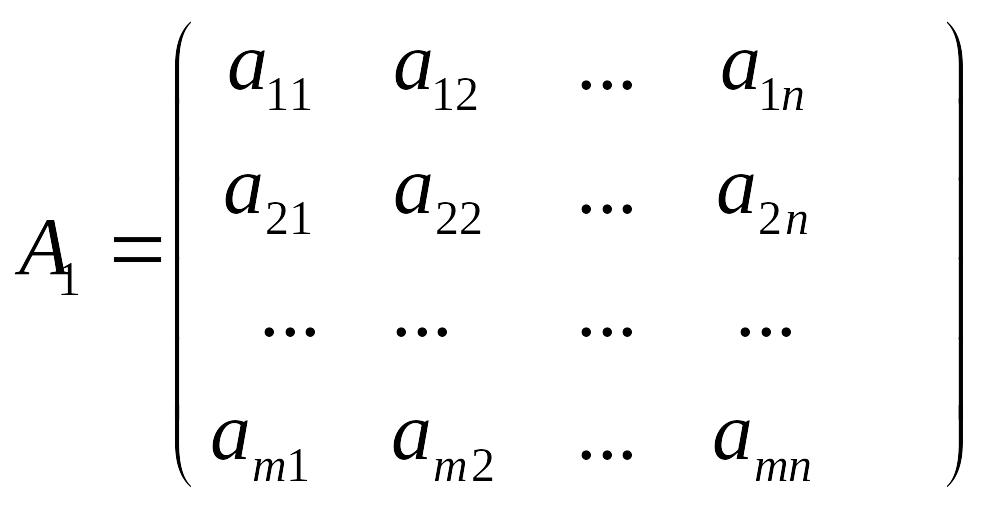 .
(2.20)
.
(2.20)
Пусть
ранг матрицы системы r
< n.
Неизвестные![]() коэффициенты при которых входят в
базисный минор матрицы системы, называются
базисными
неизвестными,
а остальные (
коэффициенты при которых входят в
базисный минор матрицы системы, называются
базисными
неизвестными,
а остальные (![]() )
– свободными
неизвестными.
)
– свободными
неизвестными.
Тогда
число линейно независимых решений
системы (1.20) равно n
– r.
При этом любые n
– r
линейно независимых решений системы
(1.20) называются ее фундаментальной
системой
решений, а любое решение однородной
линейной системы (1.20.) является линейной
комбинацией фундаментальной системы
ее решений, то есть
![]() ,
где
,
где
![]() -
фундаментальная система решений.
-
фундаментальная система решений.
Пример 1.
Найти фундаментальную систему решений однородной линейной системы
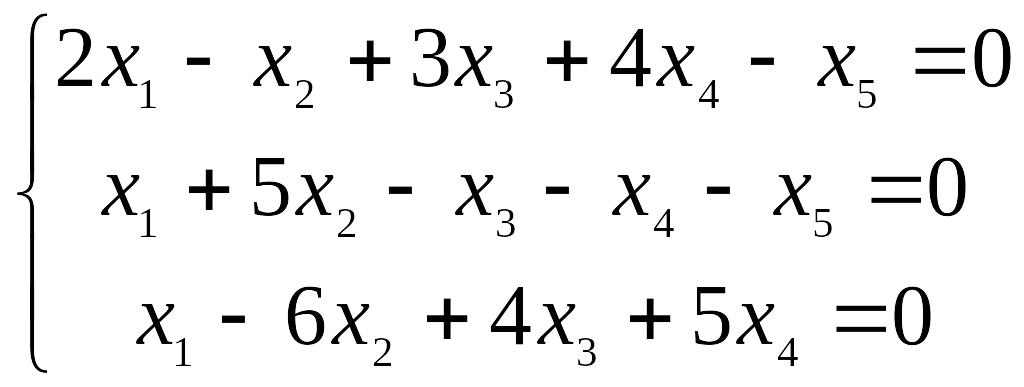 .
.
Решение.
Найдем r(A):


Выберем
в качестве базисного минора
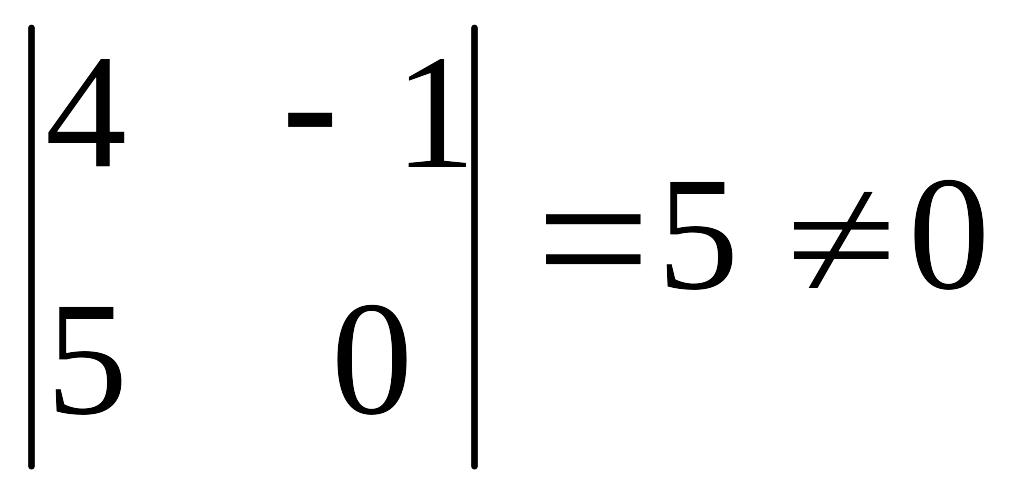 .
.
Значит, r(A) = 2. Пусть х4, х5 – базисные неизвестные, х1, х2, х3 – свободные неизвестные. Запишем для них новую систему:
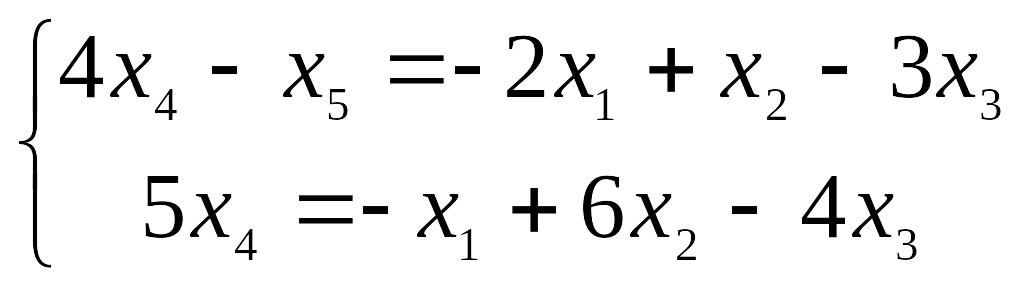 ,
,
откуда
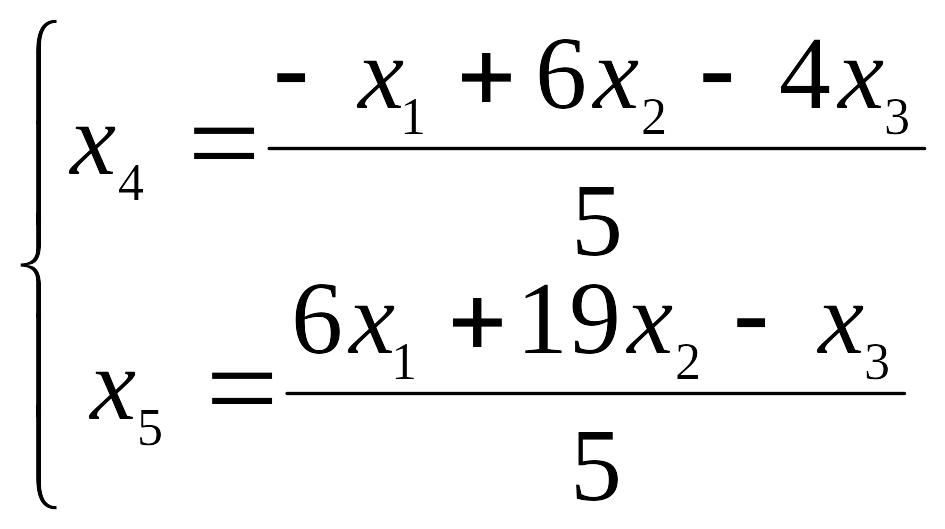 .
.
Фундаментальная система решений состоит из трех векторов. Рассмотрим три набора значений свободных неизвестных:
1) х1 = 1, х2 = х3 = 0.
Тогда х4 = -0,2, х5 = 1,2, и решение можно записать в виде строки
![]() .
.
2) х1 = 0, х2 = 1, х3 = 0.
При этом х4 = 1,2, х5 = 3,8, и следующее решение системы имеет вид
![]() .
.
3) х1 = х2 = 0, х3 = 1. Отсюда х4 = -0,8, х5 = -0,2, и последняя строка
![]() .
.
Фундаментальная
система решений, построенная при таком
выборе свободных неизвестных, называется
нормальной. Поскольку строки свободных
неизвестных
![]() линейно независимы, это гарантирует
линейную независимость решений
линейно независимы, это гарантирует
линейную независимость решений
![]() .
.
Итак, в качестве фундаментальной системы решений можно выбрать
, , .
При
этом любое решение данной системы имеет
вид:
![]() ,
где с1,
с2,
с3
– произвольные постоянные. Эта формула
задает общее решение системы.
,
где с1,
с2,
с3
– произвольные постоянные. Эта формула
задает общее решение системы.
Пример
2. Найти
фундаментальную систему решений системы
уравнений.
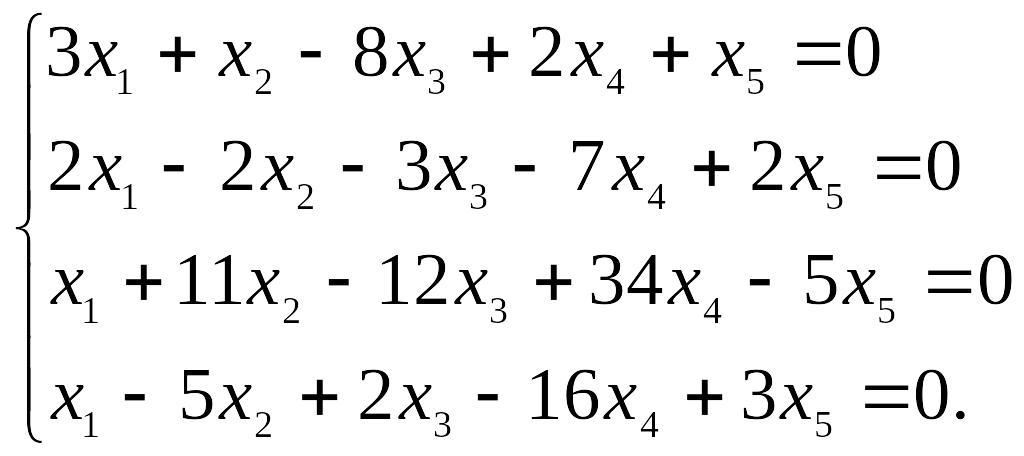
Решение. Выпишем матрицу системы, подставив последнее уравнение на первое место, затем приведем ее к ступенчатому виду:

Ранг
матрицы
![]() .
Базисный минор при переменных
.
Базисный минор при переменных
![]()
![]() отличен
от нуля:
отличен
от нуля:
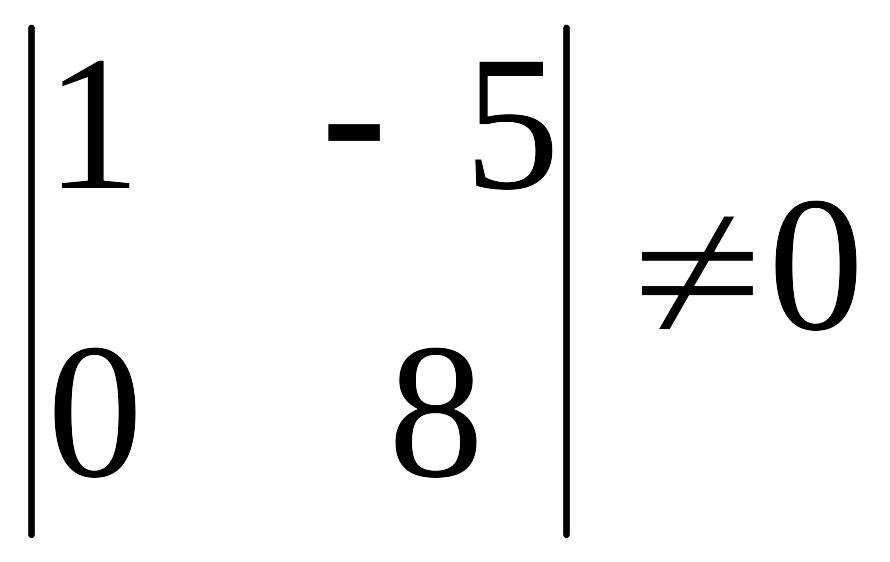 ;
выбираем
в качестве базисных переменных и выражаем
их через свободные
;
выбираем
в качестве базисных переменных и выражаем
их через свободные
![]()
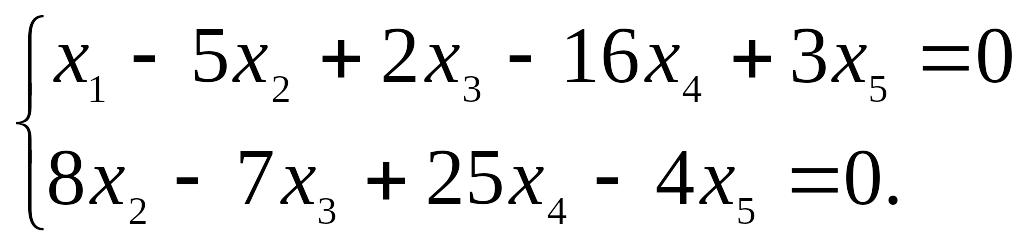
Для
получения фундаментальной системы
решений
поочередно заменяем неосновные переменные
![]() элементами строк единичной матрицы
элементами строк единичной матрицы
![]() .
.
При
![]() приведенная выше система принимает
вид:
приведенная выше система принимает
вид:
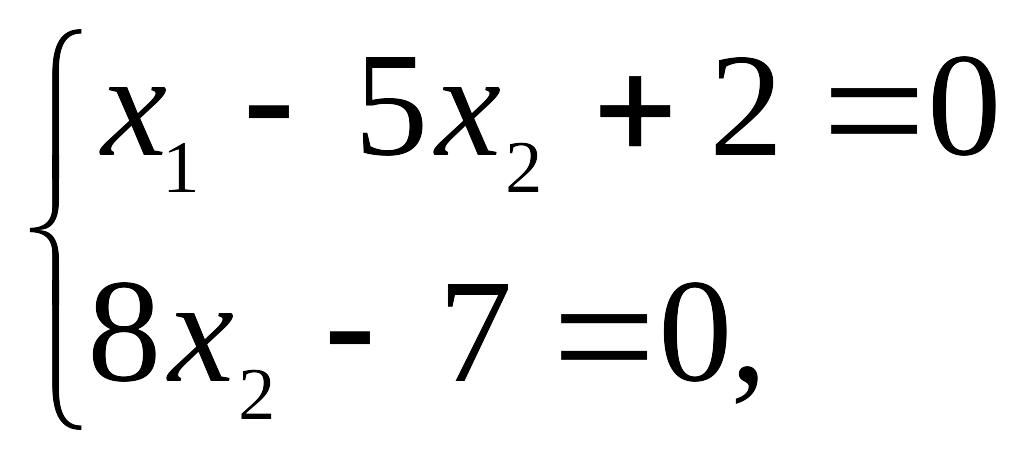 откуда
откуда
![]() ,
т.е. получаем базисное решение
,
т.е. получаем базисное решение
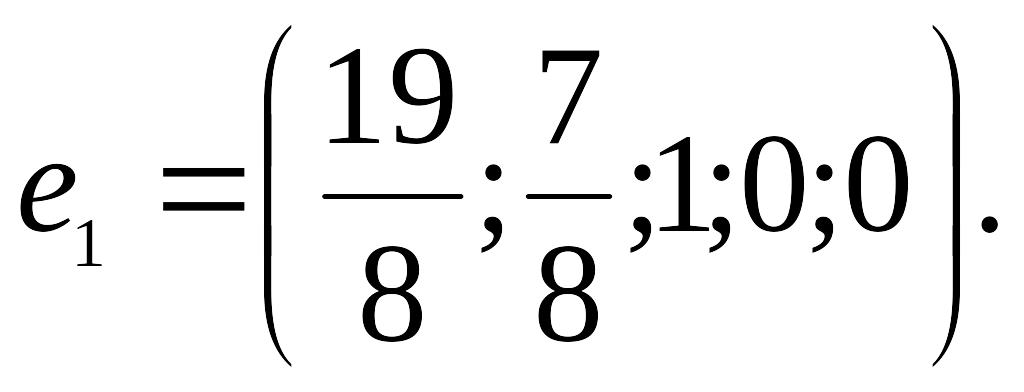
Аналогично находим еще два базисных решения:
при
![]()
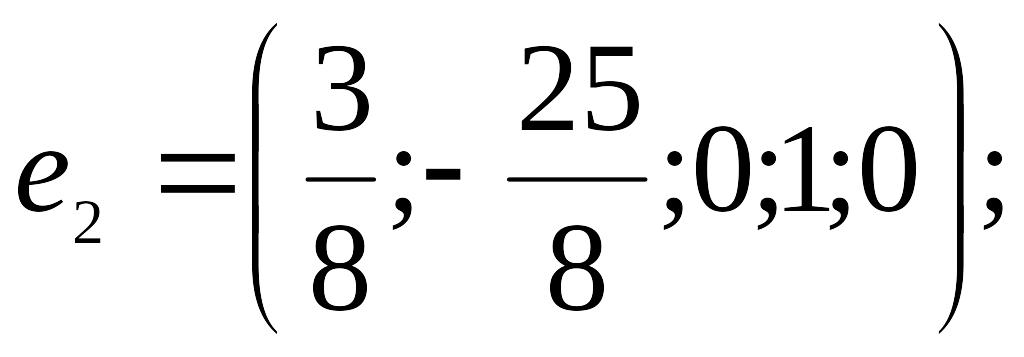
при
![]()
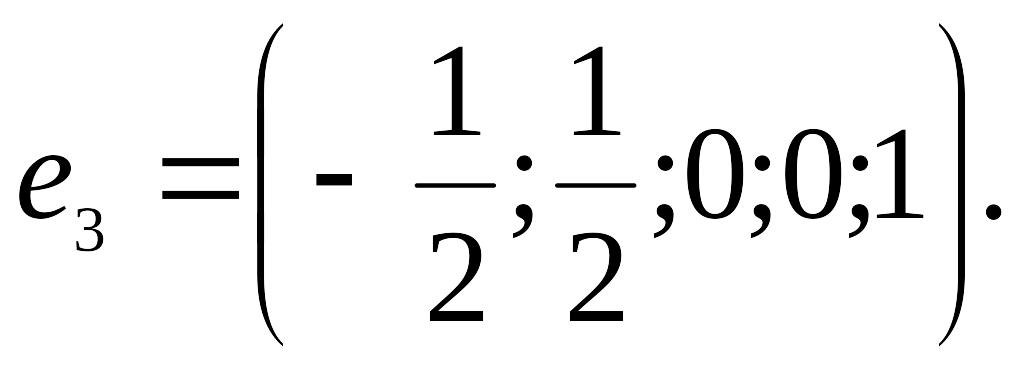
Найденные решения (векторы) образуют фундаментальную систему. Умножив компоненты решения соответственно на 8, 8, 2, получим фундаментальную систему решений с целыми компонентами.
![]() .
.
Задания для решения
Найти фундаментальные системы решений систем уравнений.
20.1.
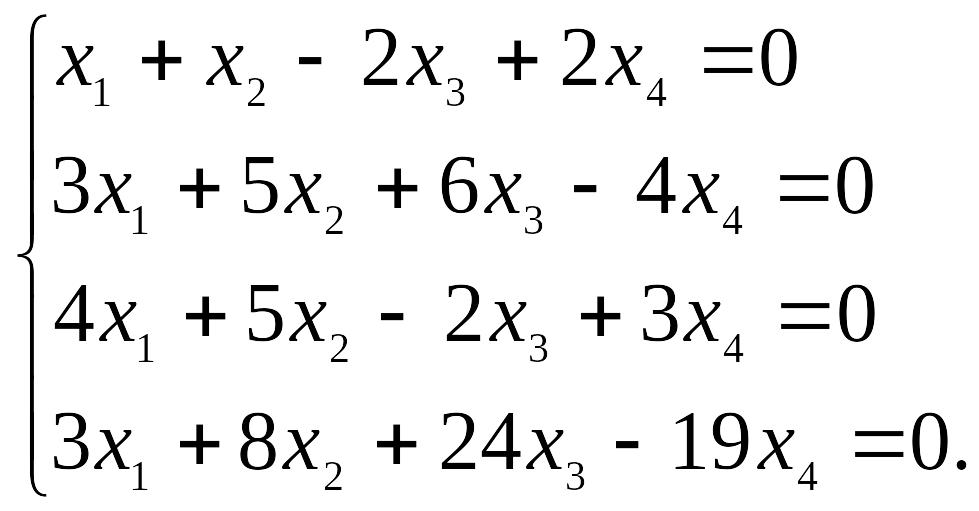 20.2.
20.2.
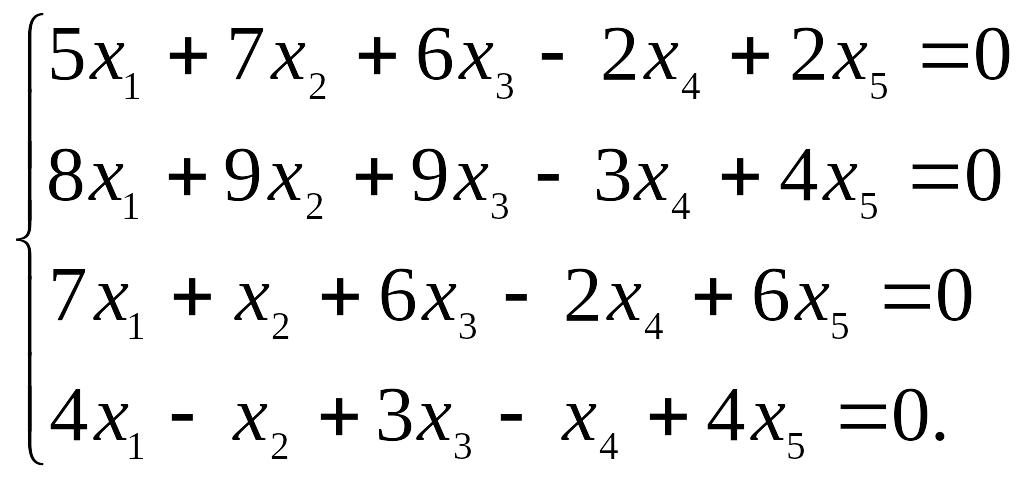
20.3.
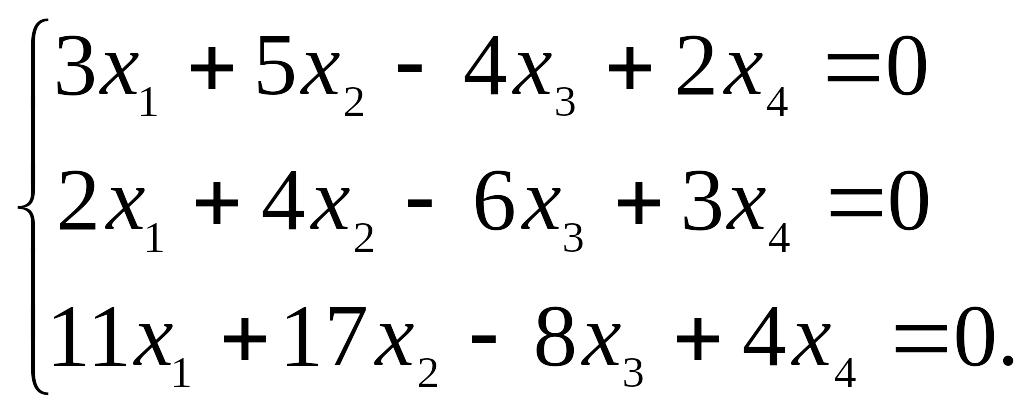 20.4.
20.4.
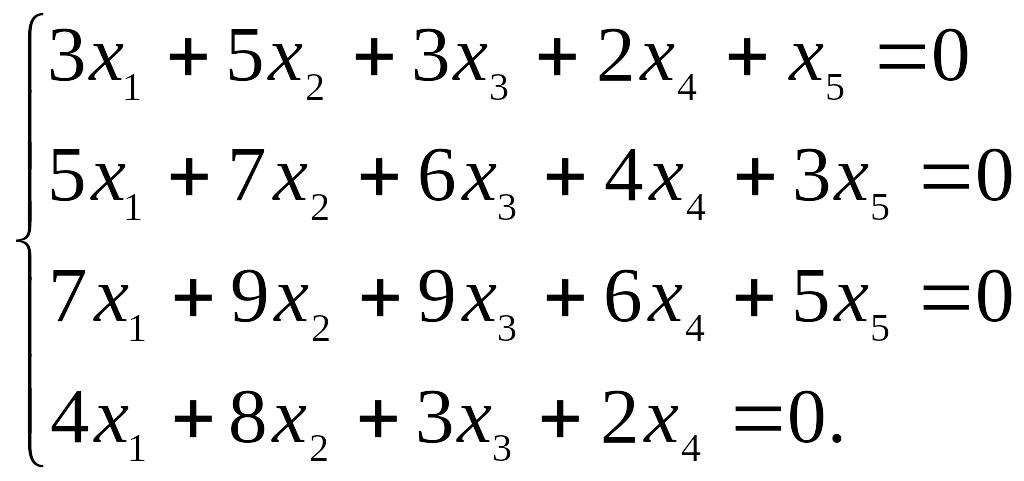
20.5.
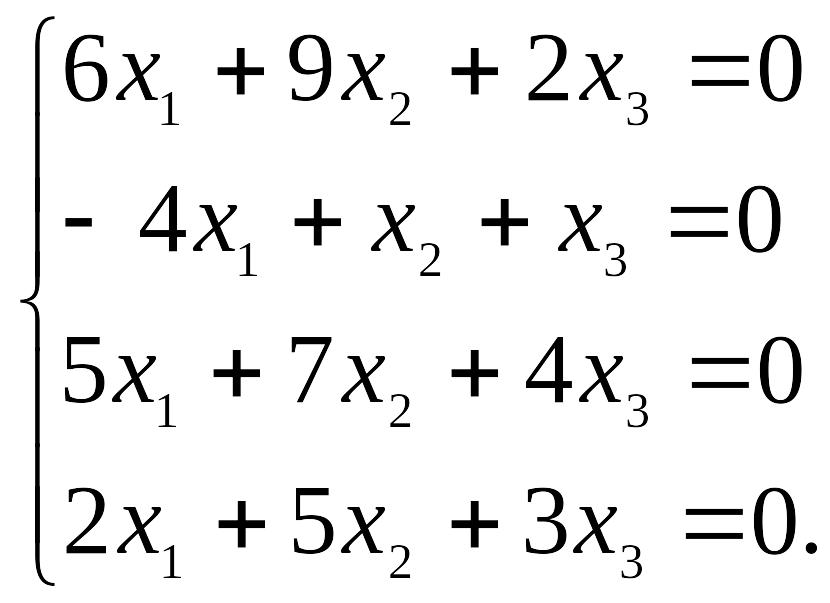
Домашнее задание
20.6. Найти все возможные наборы основных неизвестных для системы
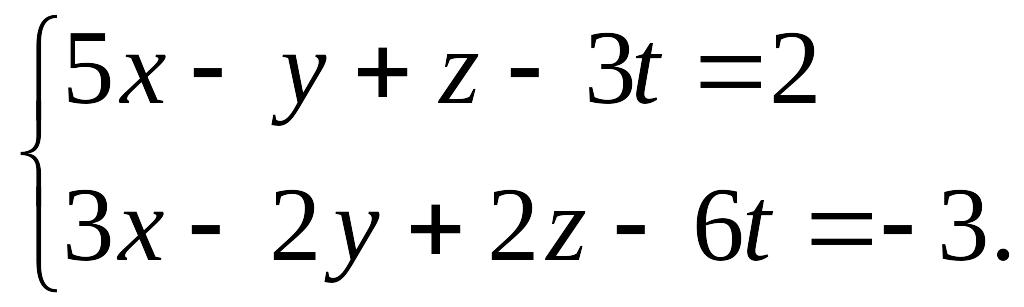
Найти фундаментальную систему решений для системы уравнений.
20.7.
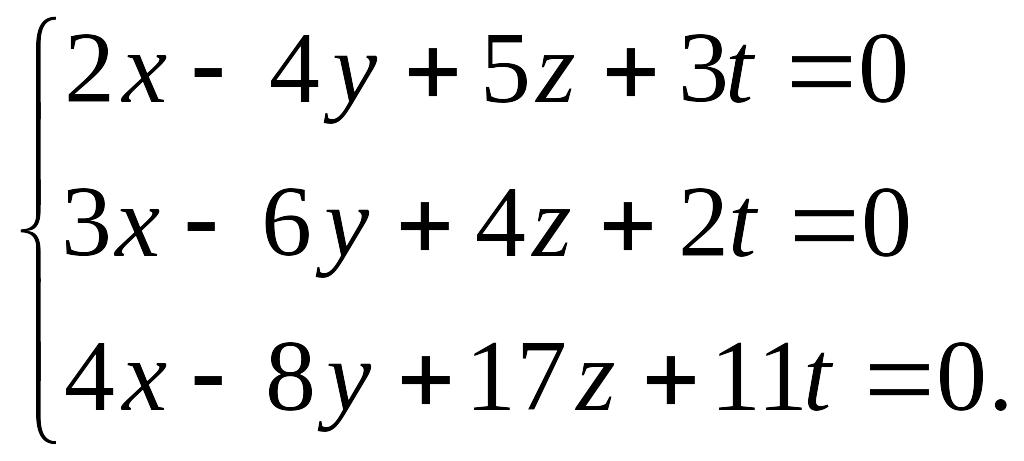
20.8.
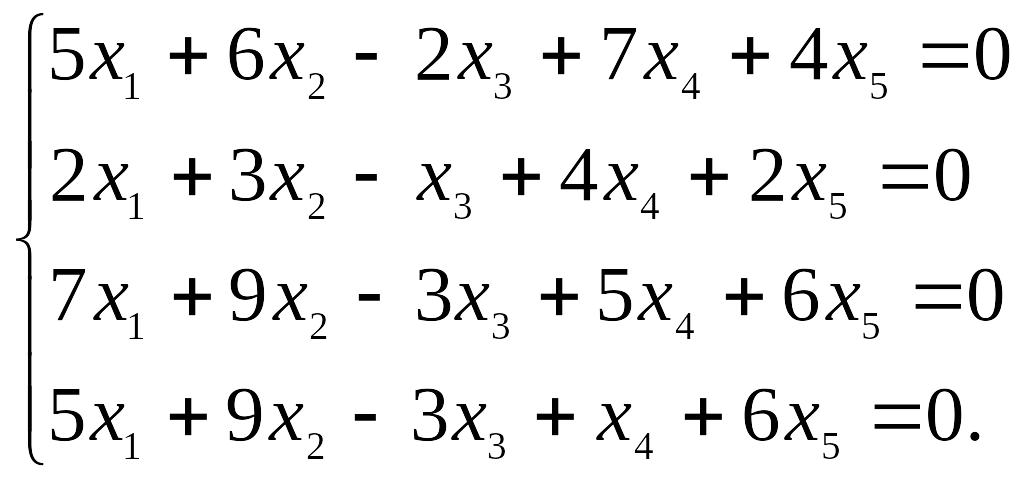
Ответы
20.1.
![]() 20.2.
20.2.
![]()
20.3.
![]() 20.4.
20.4.
![]() 20.5. Система
имеет только нулевое решение.
20.6.
20.5. Система
имеет только нулевое решение.
20.6.
![]() 20.7.
20.7.
![]() 20.8.
20.8.
![]()
21. Вычисление пределов
Краткие теоретические сведения
Пусть
функция
![]() определена во всех точках некоторого
множества X
, содержащего точку a,
кроме, быть может, самой точки a.
определена во всех точках некоторого
множества X
, содержащего точку a,
кроме, быть может, самой точки a.
Определение
1.
Число
называется
пределом
функции
![]() при
при
![]() ,
если для
любого сколь угодно малого
,
если для
любого сколь угодно малого
![]() найдется такое число
найдется такое число
![]() ,
что для всех
,
что для всех
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
![]() справедливо неравенство
справедливо неравенство
![]() .
Этот факт
записывают в таком виде:
.
Этот факт
записывают в таком виде:
![]() или
или
![]() при
при
![]() .
.
Определение предела можно записать с помощью логических символов:
![]() .
.
Пусть
функция
определена
на множестве
![]() .
.
Определение
2. Число
А называется пределом функции
при
![]() ,
если для любого
сколь угодно малого
,
если для любого
сколь угодно малого
![]() найдется такое число
найдется такое число
![]() ,
что для всех
,
что для всех
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
![]() ,
справедливо неравенство
и записывают
,
справедливо неравенство
и записывают
![]() .
.
Кратко это определение можно записать:
![]() .
.
Практическое вычисление
пределов основывается на следующих
теоремах: если существуют
![]() и
и
![]() ,
то:
,
то:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
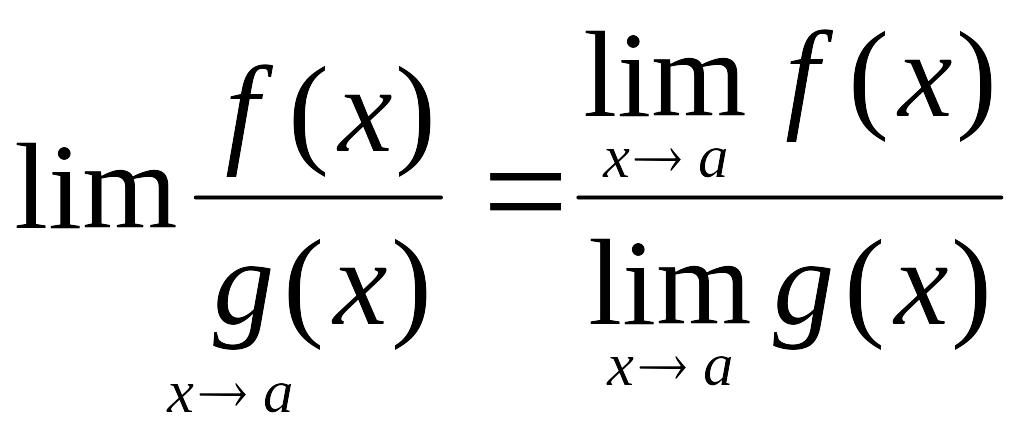 при
при
![]() ;
;
5. Для всех основных элементарных функций в любой точке их области определения имеет место равенство:
![]() .
.
При
вычислении пределов встречаются
неопределенности следующих видов:
![]() и др.
и др.
Для
раскрытия неопределенности вида
![]() часто применяют первый замечательный
предел:
часто применяют первый замечательный
предел:
![]() .
.
Для
раскрытия неопределенности вида
![]() пользуются вторым замечательным
пределом:
пользуются вторым замечательным
пределом:
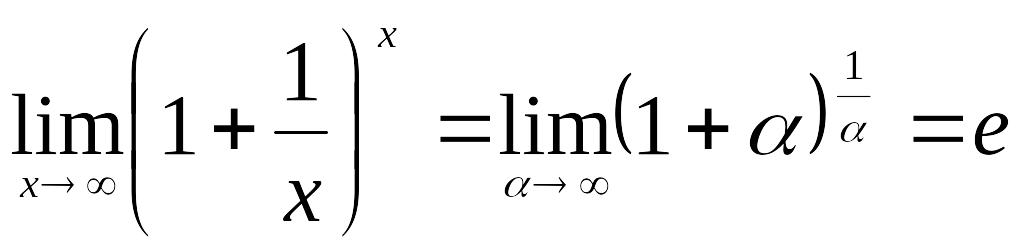 .
.
