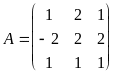Вариант № 35

1. Используя метод Крамера, решить системы уравнений:

а)

б)

в)

2. Даны матрицы:

Найти: а) А  С, С  А, С  В, А^Т  В;

б) (А), (С), ( С  А ), ( А  С );

в) матричным методом решение уравнения А  Х = В;

г) матричным методом решения систем а) и б) из задания 1.

3. Даны вершины пирамиды:

А(-3, 1, 1);

В(4, -2, 0);

С(2, 3, -2);

Д(0, 1, -1)

Найти: а) длины ребер АВ, АС, СД;

б) углы АДС, САВ, ДСВ;

в) площади граней АВС и СДВ;

г) объем пирамиды и длину высоты, опущенной из точки А.

4. Дан треугольник на плоскости с вершинами в точках А(-3, 2), В(1, 0), С(6, -4).

Найти: а) уравнения всех его сторон;

б) уравнения всех высот и всех медиан;

в) точку пересечения высот и точку пересечения медиан;

г) длину одной из высот треугольника.

4. Составить уравнение прямой, проходящей через точки:

а) А(-3, 5, 7), В(1, 2, 1);

б) А( 3, 3, 5), В(4, 3, 7);

в) А(0, -1, 2), В( 5, 10, 5).

4. Через точку А(2, 2, 1) провести прямую:

а) параллельную прямой ;

б) перпендикулярную векторам:

7. Составить уравнение плоскости, проходящей через:

а) точки А(7, 10, 3), В(0, 4, 1), С(8, 1, 1);

б) точку А(-4, 5, 3) и прямую ;

в) две пересекающиеся прямые и ;

г) две параллельные прямые и .

8. Найти точку пересечения прямой и плоскости:

а) ;

б) .

8. Найти точку Q, симметричную точке Р(4, 5, 1) относительно плоскости

2х - 3у + z - 1 = 0.

8. Найти точку Q, симметричную точке Р(1, 0, 2) относительно прямой

.

8. Построить плоскости:

х + 2у + 2z - 4 = 0, x + 4z - 8 = 0, x + 3 = 0, 3x - 5y = 0.

Вариант № 36

1. Используя метод Крамера, решить системы уравнений:

а)

б)

в)

2. Даны матрицы:

Найти: а) А  С, С  А, С  В, А^Т  В;

б) (А), (С), ( С  А ), ( А  С );

в) матричным методом решение уравнения А  Х = В;

г) матричным методом решения систем а) и б) из задания 1.

3. Даны вершины пирамиды:

А(-2, 2, 3);

В(-0, 4, 5);

С(1, -3, -1);

Д(2, 1, 0)

Найти: а) длины ребер АВ, АС, СД;

б) углы АДС, САВ, ДСВ;

в) площади граней АВС и СДВ;

г) объем пирамиды и длину высоты, опущенной из точки А.

4. Дан треугольник на плоскости с вершинами в точках А(6, -1), В(1, 4), С(1, -1).

Найти: а) уравнения всех его сторон;

б) уравнения всех высот и всех медиан;

в) точку пересечения высот и точку пересечения медиан;

г) длину одной из высот треугольника.

5. Составить уравнение прямой, проходящей через точки:

а) А(3, -1, 4), В(1, 6, 0);

б) А( 2, 4, 5), В(1, -1, 5);

в) А(1, 3, 0), В( 0, 1, 1).

6. Через точку А(4, 5, 2) провести прямую:

а) параллельную прямой ;

б) перпендикулярную векторам:

6. Составить уравнение плоскости, проходящей через:

а) точки А(1, 3, 0), В(-1, 1, 1), С(0, 6, 7);

б) точку А(5, 0, 1) и прямую ;

в) две пересекающиеся прямые и ;

г) две параллельные прямые и .

6. Найти точку пересечения прямой и плоскости:

а) ;

б) .

6. Найти точку Q, симметричную точке Р(4, 2, -1) относительно плоскости

х - 8у +2 z - 1 = 0.

6. Найти точку Q, симметричную точке Р(1, -1, 2) относительно прямой

.

11. Построить плоскости:

4х + у +2 z -8 = 0, 3х -5 y + 15 = 0, у - 3 = 0, 2y - 5z = 0.