§ 2.8. Визначення структури кристала
Основне завдання, що створюють при дослідженні структури кристала, - визначення взаємного розташування атомів у просторовій решітці кристала. Найбільшу інформацію про структуру кристала можна одержати за допомогою дифракційних методів рентгено-, електронно- і нейтронографії й електронній мікроскопії. Останнім часом до них додалися протонографія й мєссбауерографія й були створені так називані «прямі методи», що дозволяють одержати за допомогою ЕОМ зображення структури досліджуваного кристала.
Найбільш відомий метод визначення структури кристала - рентгенівський. Успішному розвитку рентгеноструктурного аналізу сприяла сумірність довжини хвилі рентгенівських променів з міжатомними відстанями в решітці. При проходженні рентгенівських променів через кристалічну решітку вони випробовують дифракцію.
Розглянемо взаємодію електромагнітної хвилі рентгенівського випромінювання з атомом речовини. В однорідному електричному полі відбувається поляризація атома, тобто поділ позитивних і негативних зарядів. У постійному полі поляризація' стаціонарна, але якщо поле змінне, то поляризація міняється відповідно до частоти, у результаті чого виникають коливання позитивних і негативних зарядів (рисунок 2.23).
Завдяки індукованому коливальному руху зарядів атом розсіює падаюче на нього електромагнітне випромінювання. Коливаючи один щодо одного заряди випромінюють електромагнітні хвилі з такою же частотою, з який вони самі коливаються. Випромінювані хвилі поширюються в усіх напрямках (рисунок 2.24). Процес поглинання й випромінення хвиль називають розсіюванням або дифракцією падаючих рентгенівських променів. Кожен атом решітки стає джерелом випромінювання. Хвилі, випромінювані атомами, в результаті інтерференції можуть послаблятися й підсилюватися. Послаблення й посилення хвиль залежить тільки від відстані між атомами й від частоти падаючого випромінювання. Інтерферуючі промені підсилюють один одного в тому випадку, якщо різниця їхнього ходу дорівнює цілому числу довжин хвиль. Загальні умови дифракції рентгенівських променів у реальних кристалах сформулювали англійські фізики У. Г. Брегг, У. А. Брегг і незалежно від них - росіянин кристаллограф Ю. В. Вульф.
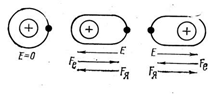
Рисунок 2.23 - Поляризація атома, поміщеного в електромагнітне поле: Fe й Fa - сили, що діють на електрони і ядро відповідно
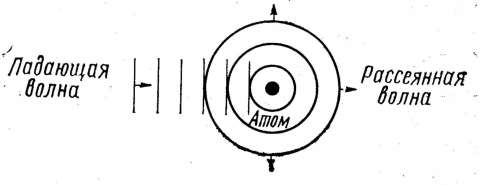
Рисунок 2.24 - Схема виникнення вторинних рентгенівських променів
На систему паралельних атомних площин з мiжатомною відстанню d під кутом θ падає пучок рентгенівських променів з довжиною хвилі λ. Під тим же кутом виникає пучок відбитих променів (рисунок 2.25). Інтенсивність відбитих променів має помітну величину в тому випадку, якщо промені, відбиті різними площинами, у результаті інтерференції підсилюють один одного. Різниця ходу променів MON і М'О'N' дорівнює PO'+O'Q, причому PО' = О'QММ' – фронт падаючих променів, NN'– фронт відбитих променів, а ОР ┴ М'О', OQ┴О'N. Із прямокутного трикутника OO'Р знаходимо, що РО' = d·sinθ. Різниця ходу променів складає 2d·sinθ. Для інтерференційного підсилення повинна виконуватись умова 2d·sinθ = пλ, яка називається умовою Вульфа – Брегга, де п – порядок відбиття.
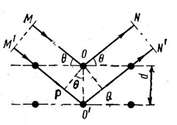
Рисунок 2.25 - Ілюстрація закону Вульфа – Брегга
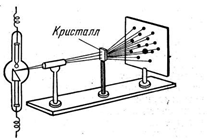
Рисунок 2.26 - Схема установки в методі нерухомого монокристалла
Який би не був кут падіння рентгенівських променів і порядок відбиття, завжди знайдуться довжини до хвиль, що задовольняють умові Вульфа - Брегга. Тільки такі хвилі з такими значеннями довжини можуть відбиватися від розглянутих атомних площин. Ефективними, з погляду відбиття, є тільки такі площини, на яких частинки, що утворюють кристал, розташовані досить часто. Дифракційну картину можна розглядати як сукупність рентгенівських променів, що перетерпіли відбиття на таких атомних площинах. Умова Вульфа - Брегга є основою для розрахунків у методі рентгеноструктурного аналізу кристалів.
Якщо направити на кристал потік рентгенівських променів і помістити за кристалом фотопластинку, то на ній з'являться окремі плями (рисунок 2.26). Це дифракційна картина рентгенівських променів. Кожному елементу й кожній хімічній сполуці; відповідають певні просторові решітки й, отже, своя рентгенівська інтерференційна картина, що залежить від структури кристала. Вивчаючи взаємне розташування плям або ліній на пластинці й вимірюючи їхню інтенсивність, можна приписати приналежність даної рентгенограми певному елементу.