3.3. Достоинства и недостатки растровой графики

К достоинствам растровой графики относятся:

• Аппаратная реализуемость.

К настоящему моменту изобретены и доведены до массового производства определенные классы устройств (сканеры, цифровые фотокамеры), которые позволяют автоматизировать процедуру преобразования графической информации в цифровую форму.

• Программная независимость.

Характер информации (совокупность чисел, организованных в двухмерную матрицу), который требуется для хранения растрового изображения, позволяет создавать стандартные форматы. Эти форматы «понимают» практически все программы, работающие с изображениями: редакторы растровой и векторной графики, программы верстки, браузеры и даже операционные системы.

• Фотореалистичность изображений.

Как правило, характерными особенностями фотореалистичности являются множество цветов, градиенты, сложное освещение, наличие мягких тоновых переходов (дымка, туманы, облачность и т.п.).

Недостатки растровой графики:

• Значительный объем файлов.

Основные способы уменьшения объема растровых изображений состоят в оптимизации параметров, определяющих объем, в разумном кадрировании и использовании алгоритмов сжатия (выборе соответствующих форматов файлов).

• Сложности трансформирования растровых изображений.

Любые трансформации растровой графики (кроме ортогональных поворотов и зеркальных отражений по горизонтали и вертикали) сопряжены с проблемами (погрешностями, искажениями и деформациями), вызываемыми дискретной, или сетчатой, структурой изображения.

Кроме этого, в результате трансформирования, особенно с использованием алгоритмов интерполирования, помимо погрешностей детализации, у изображений всегда ухудшается резкость.

• Аппаратная зависимость.

Основной причиной этого недостатка является то, что практически все внешние устройства (мониторы, принтеры и фотонаборные автоматы) визуализируют изображения средствами битовой карты. Любое изображение строится из совокупности каких-либо элементов (например, пикселов экрана, капель чернил, точек тонера, пятен, создаваемых лазерным лучом), поэтому каждое из таких устройств характеризуется собственным разрешением. Этот параметр играет существенную роль при печати изображения, так как происходит наложение дискретной сетки изображения на дискретную сетку устройства, что не всегда благоприятно для окончательного результата (например, возможно появление паразитного узора - муара).

Таким образом, перед созданием изображения (например, перед сканированием) пользователь уже должен представлять условия вывода изображения на визуализирующих устройствах.

Векторная графика - один из способов представления графической информации с помощью совокупности кривых, описываемых математическими формулами

4. Основы векторной графики

4.1. Общие сведения

Векторы представляют собой математическое описание объектов относительно точки начала координат. Проще говоря, чтобы компьютер нарисовал прямую линию, нужны координаты двух точек, которые связываются по кратчайшему пути. Для рисования дуги кроме координат двух точек необходимо задать еще и радиус и т.д.

Векторная иллюстрация - это набор геометрических объектов, построенных на основе кривых Безье, или примитивов (прямоугольников, окружностей, эллипсов, линий), поэтому векторная графика называется объектно-ориентированной.

М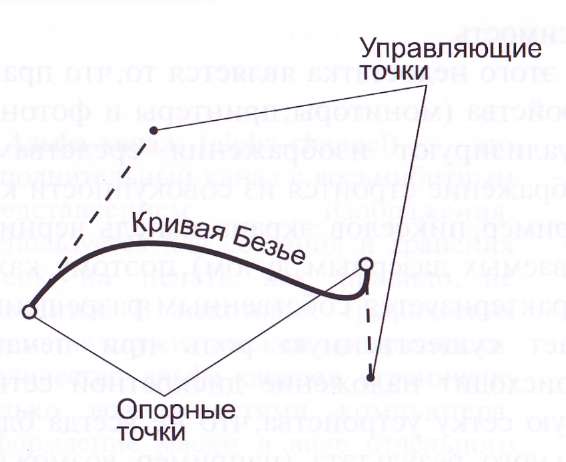 етод построения кривых Безье основан на использовании пары касательных (управляющих линий), проведенных к сегменту кривой в его окончаниях

Рис. 9. Кривая Безъе

Если рассмотреть произвольный простейший отрезок кривой Безье между двумя несовпадающими точками (рис. 9), то для его описания потребуется всего восемь цифр: ХY-координаты первой опорной точки, ХY-координаты первой управляющей точки, ХY-координаты второй опорной точки и ХY-координаты второй управляющей точки.

На форму кривой влияют угол наклона касательной и длина ее отрезка.

Математический аппарат построения кривых Безье позволяет на основе этой информации построить и визуализировать линию.

Линия - элементарный объект векторной графики. Как и любой объект, линия обладает свойствами: формой (прямая, кривая), толщиной, цветом, начертанием (сплошная, пунктирная). Окончание линии (то есть ее форма в конечном узле) также выступает одним из свойств с изменяемыми параметрами.

Простейшая незамкнутая линия ограничена двумя точками, именуемыми узлами. Узлы имеют ряд свойств, параметры которых влияют на форму конца линии и характер сопряжения с другими объектами. Все прочие объекты векторной графики, в том числе самые сложные, составляют из линий (рис. 10,а).

Замкнутые линии приобретают свойство заполнения. Охватываемое ими пространство может быть заполнено другими объектами (текстуры, карты) или выбранным цветом (10, б). Заполнение бывает растровым и векторным. В последнем случае иногда используют элементы фрактальной графики, являющейся частным случаем векторной. Основные языки программирования при выводе графических примитивов также используют понятия векторной графики.

Для построения объектов векторной графики используют инструменты рисования линий и управления заполнением контуров. Простые объекты могут взаимодействовать различными способами, в том числе с применением булевых операций объединения, вычитания и пересечения.

Эффекты, применямые к объектам векторной графики, воздействуют на свойства линии, заполнения и узлов. По сути дела, в программах векторной графики все эффекты являются модификаторами. Модификатор описывает математическими методами параметры изменения свойств исходного объекта, не затрагивая его основ. Именно на этом базируется возможность возврата к исходному состоянию объекта.

Рис. 10. Пример векторного изображения