4. Применения полупроводниковых лазеров

Полупроводниковые лазеры находят сегодня целый ряд важных применений в различных областях. Впервые эти лазеры в больших масштабах использовались в качестве оптической считывающей головки в компакт-дисковых системах. Теперь эта область применения расширилась и включает в себя оптические диски, используемые как постоянные или одноразовые запоминающие устройства. Для этих применений используются GaAs-лазеры, однако предпринимаются большие усилия для разработки полупроводниковых лазеров видимого диапазона, поскольку более короткая длина волны позволяет считывать диски с более высокой поверхностной плотностью записи. В лазерах видимого диапазона в качестве активной среды применяется тройной сплав GaInP (или четверной сплав AlGaInP), а для р- и n-облаcтей — GaAs. Выбором подходящего параметра состава можно согласовать решетки обоих сплавов с GaAs, и к настоящему времени достигнута надежная работа при комнатной температуре в красной области спектра (λ = 680 нм) на основе GalnP. Кроме того, эти лазеры широко применяются в волоконнооптической связи, причем опять же с GaAs, в то время как в будущем, наверное, для этой цели лучше подойдет лазер на четверном сплаве InGaAsP. Для применений в связи срок службы любого компонента должен составлять как минимум около 10⁵ ч (т. е. больше 10 лет). В настоящее время срок службы промышленных устройств составляет 10⁴ ч, а экспериментальных около 5*10⁵ ч ¹⁾. В настоящее время полупроводниковые лазеры на GaAs широко применяются для накачки Nd : YAG-лазеров в конфигурации с продольной накачкой. Для получения более высоких мощностей стержень из Nd : YAG можно также накачивать в поперечной конфигурации линейкой диодных лазеров. Как уже отмечалось, выходная мощность полоскового диодного лазера ограничена оптическим разрушением грани до типичного значения около 50 мВт. С целью повышения мощности были разработаны линейки диодов с отдельными лазерными каналами, достаточно близко расположенными друг к другу, так что излучение всех этих каналов становится связанным, а фазы— синхронизованными. Таким путем была получена мощность около 2 Вт от линейки из 40 лазерных каналов. В заключение можно сказать, что для приложений полупроводниковые лазеры в настоящее время, по-видимому, играют наиважнейшую роль. Учитывая продолжающееся быстрое развитие этих лазеров, можно ожидать, что их роль в будущем значительно возрастет.

¹⁾ Следует заметить, что поскольку 1 год равен примерно 9000 ч, для оценки столь длительного срока службы необходимо применять так называемые тесты ускоренного старения. При этом ожидаемый срок службы при комнатной температуре экстраполируется из результатов ресурсных испытаний при повышенной температуре (при которой срок службы заметно короче).

5. Упрощенная теория полупроводникового лазера

Рассмотрим полосковый полупроводниковый ДГ-лазер. Пусть А — площадь полоски, a d — толщина активной среды в направлении, перпендикулярном плоскости перехода. Обозначим скорость, с которой электроны (и дырки) инжектируются в единичный объем активного слоя, через R_p. Для вычисления этой скорости инжекции заметим вначале, что та часть инжектированных носителей, которые не рекомбинируют излучательно, испытывает безизлучательную электрон-дырочную рекомбинацию в основном на границах перехода. Следовательно, эту часть носителей можно рассматривать как если бы они вовсе не были инжектированы в активную область. Таким образом, нетрудно показать, что при данном токе I через переход R_p дается выражением

где η_i — внутренняя квантовая эффективность, а е — заряд электрона. Прежде чем продолжить рассмотрение, необходимо подчеркнуть, что обсуждаемый здесь случай отличается от всего того, что имеет место во всех лазерах, которые мы до сих пор изучали, по крайней мере в трех следующих отношениях: 1) Величинами, которыми необходимо теперь пользоваться, являются плотность носителей N, а не обычная инверсия населенностей, и скорость инжекции R_p вместо произведения W_p(N_t – N), определяющего накачку. 2) В полупроводнике максимальный коэффициент усиления a_g можно приближенно записать в виде

где σ — сечение вынужденного излучения, а N—постоянная (для GaAs при Т = 300 К имеем σ ≈ 1,5*10^-16 см² и N^/ ≈ 1,5*10¹⁸ носителей/см³). Заметим, что, как следует из (6.41), при N<n^/ усиление в полупроводнике отсутствует. Согласно разд. 6.6.1.4, физическое объяснение этого состоит в том, что если инжектировано недостаточное количество носителей, то квазиуровни Ферми не удовлетворяют условию Е_fc – Е_fv > E_g и, следовательно, в полупроводнике усиления нет. 3) Поперечная ширина поля в резонаторе d' существенно больше, чем толщина активной области d (например, в GaAs мы имеем d^’ ≈ 0,8 мкм при d ≈ 0,1 мкм). В этом случае, полагая, что торцевые грани полупроводника служат зеркалами резонатора, мы получаем следующие скоростные уравнения для плотности носителей N и полного числа фотонов в данной моде q:

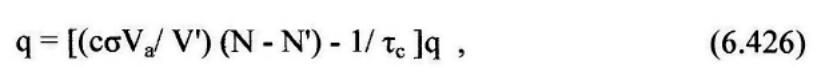
где с=с₀/λ, а

здесь U — поле в резонаторе (нормированное на свое максимальное значение) и интегрирование производится по всему распределению поля; τ_r — время жизни при излучательной рекомбинации (при сделанных выше предположениях все носители в активном объеме рекомбинируют излучательно);

(здесь интеграл берется по объему активной среды).

Условие порога генерации теперь нетрудно получить, полагая N = 0 и q = 0 в левых частях уравнений (6.42) и q = 0 в правой части (6.42а). Тогда из уравнения (6.42б) с помощью (5.136) (заметим, что, согласно (5.11), в нашем случае L^’ = nl) получаем критическую инверсию

где l— длина полупроводника. Сравнивая это выражение с (5.26), мы получаем следующее: 1) в выражение (6.44) входит дополнительный член N', введенный в (6.41); 2) член γ/σl выражения (5.26) теперь входит с множителем V^’/V_a благодаря тому, что ширина поперечного распределения поля больше толщины активного слоя. На самом деле, используя выражения (6.43а) и (6.436), можно записать V^’/V_a ≈ d'/d, а выражение (6.44) принимает простой вид:

Это выражение показывает, что для описания вынужденного излучения фотонов в данной моде можно определить эффективное сечение σ_эфф = σ/(d/d'). Так как d « d', мы имеем σ_эфф « 0. Критическую скорость накачки находим из выражения (6.42а):

Отсюда, используя выражения (6.44а) и (6.40), получаем следующие выражения для пороговой плотности тока J_nop = I_пор/А:

Заметим, что если в этом выражении присутствовал бы только множитель во вторых квадратных скобках, то величина J_пор уменьшалась бы с уменьшением толщины d активного слоя. Однако когда d становится слишком малой, величина γd’/σld в выражении (6.46) становится больше N' в случае d'/d » 1 из этого выражения следует, что J_пор не зависит от d. На самом деле, как уже говорилось в разд. 6.6.3, когда толщина активного слоя становится очень малой, поле резонатора настолько далеко заходит в р - и n-области диода,

что испытывает существенные потери в этих областях. При этом следует ожидать, что при малых d плотность тока J_пор должна увеличиваться с уменьшением d. Таким образом, существует минимальная величина J_пор, причем соответствующее ей значение d оказывается равным 0,1 мкм (см. рис. 6.46). Из уравнений (6.42) можно также получить значения N₀ и q₀ выше порога в непрерывном режиме, полагая N^/ = 0 и q^/ = 0. Таким образом, мы имеем

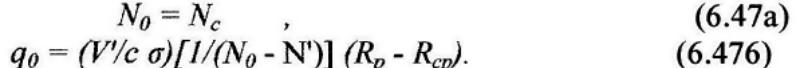
Выражение (6.47a) показывает, что и в этом случае инверсия в непрерывном режиме остается фиксированной на пороговом уровне. Из выражения (6.476) с учетом (6.44) и (6.40), а также того факта, что V_q ≈ Ad, получаем

Отсюда с помощью (5.20) находим окончательное выражение для выходной мощности через одно зеркало:

которое имеет простое объяснение. Действительно, член η_i (I - I_пор)/е представляет собой число носителей, инжектированных в активный объем за вычетом порогового значения. При этом выделяющаяся мощность равна просто этой величине, умноженной на энергию фотона hν. Наконец, выходная мощность равна выделяющейся мощности, умноженной на эффективность связи η_c = γ₂/2γ. Из выражения (6.49) теперь находим дифференциальный КПД:

где V — напряжение источника питания. Заметим, что из-за небольшого падения напряжения на внутреннем сопротивлении диода величина hv/eV несколько меньше единицы. Будем называть это электрическим КПД. Таким образом, дифференциальный КПД оказывается равным произведению внутренней квантовой эффективности на электрический КПД и на эффективность связи. Если оба торца имеют одинаковые коэффициенты отражения JR, а α – коэффициент поглощения в полупроводнике благодаря внутренним потерям, то

и

Сумма выходных мощностей из обоих торцов Р и соответствующий дифференциальный КПД в этом случае можно получить из выражений (6.49) и (6.50) , Заменяя γ₂ на γ₁ + γ₁ = - 2 ln R и подставляя у из выражения (6.516). При этом получаем следующие выражения:

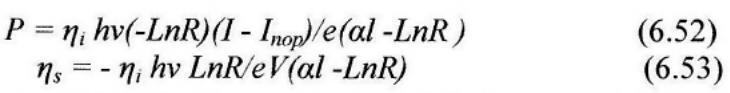
Для наших численных оценок мы используем следующие значения, характерные для ДГ-лазера на GaAs: d = 0,1 мкм, d^’ = 0,8 мкм, σ ≈ 1,5*10^-16 см², N' = 1,5*10¹⁸ см³, η_i ≈ 1; τ_r ≈ 4 нc, l = 250 мкм, a = 10 см^-1. Кроме того, предположим, что (hv/eV)≈ 0,8 и коэффициенты отражения обоих торцов равны коэффициенту отражения свободных поверхностей (R ≈ 35%). Тогда из выражения (6.51б) находим γ = 1,25, так что пороговая плотность тока в соответствии с (6.46) имеет значение J_nop ≈ 1,6*10³ А/см², которое хорошо согласуется с экспериментальными результатами. Из выражения (6.53) находим, что дифференциальный КПД σ_s ≈ 67 %; это значение опять же хорошо соответствует лучшим из полученных результатов.