1.4. Квазиуровни Ферми

Рассмотрим теперь случай, когда из валентной зоны в зону проводимости заброшено много электронов. Поскольку внутризонные переходы имеют значительно большую скорость, чем межзонные, внутри каждой зоны сразу установится тепловое равновесие, хотя полупроводник как целое и не находится в тепловом равновесии. Поэтому можно по отдельности говорить о вероятностях заполнения для валентной зоны f_v и для зоны проводимости f_c которые даются выражениями, имеющими тот же вид, что и выражение (6.29), а именно

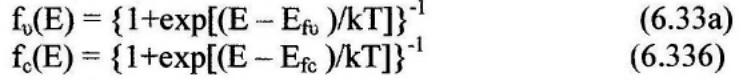
где Е_fv и E_fc — энергии так называемых квазиуровней Ферми соответственно валентной зоны и зоны проводимости. Из этих выражений, а также наших предварительных замечаний (см. рис. 6.37,6) видно, что, например, при T=0К эти уровни обозначают границы между полностью заполненными и абсолютно пустыми областями энергий внутри каждой зоны. Е_fv и E_fc, очевидно, зависят от количества электронов, заброшенных при накачке в зону проводимости. Действительно, чем больше этих электронов, тем выше E_fc и ниже Е_fv.

Рассмотрение полупроводникового лазера сильно упрощается при использовании понятия квазиуровней Ферми, поскольку для каждой зоны необходима лишь одна величина, описывающая вероятность заполнении большого (как правило) числа участвующих в генерации уровней. В качестве примера полезности этого понятия мы можем сразу получить необходимое условие для лазерной генерации, налагая требование, чтобы число актов вынужденного излучения было больше числа актов поглощения (избыток необходим для компенсации потерь в резонаторе). Оба указанных процесса пропорциональны произведению числа фотонов в резонаторе и коэффициенту В данного перехода. Однако вероятность вынужденного излучения будет также пропорциональна произведению вероятности заполнения верхнего уровня и вероятности того, что нижний уровень будет свободным, в то время как вероятность поглощения будет пропорциональна произведению вероятности заполнения нижнего уровня и вероятности того, что верхний уровень окажется свободным. Таким образом, чтобы получить вынужденное излучение на переходе между уровнем с энергией Е₂ в зоне проводимости и уровнем с энергией E₁ в валентной зоне, мы должны потребовать выполнения неравенства

т.е. чтобы

Из этого неравенства с учетом выражений (6.33) получаем

здесь ν — частота испускаемого фотона. Заметим, что при Т = 0 К условие (6.36) нетрудно получить из рис. 6,37, б путем непосредственного геометрического рассмотрения. Однако предшествующий вывод убеждает в том, что данное соотношение справедливо при любой температуре (до тех пор, пока остается применимым понятие квазиуровней Ферми). Напомним, что условие (6.36) является результатом требования, чтобы процессы вынужденного излучения преобладали над процессами поглощения. В этом отношении неравенство оказывается эквивалентным общему условию (5.25), выведенному для четырехуровневого лазера. Наконец, заметим, что энергия излучаемого фотона должна, очевидно, быть больше ширины запрещенной зоны E_g. Таким образом, мы приходим к следующему условию:

которое приблизительно устанавливает ширину контура усиления полупроводника. Обычно эта ширина оказывается довольно большой (A_v 400 см^-1), хотя она и не столь велика, как в случае лазера на красителе (A_v 2000 см^-1; см. рис. 6.29), с которым полупроводниковый лазер оказывается в некоторых аспектах очень схож (ср., например, схемы накачки на рис. 6.40 и рис, 6.31), Заметим, что, поскольку разность E_fc – Е_fv увеличивается с ростом числа заброшенных в зону проводимости электронов, некоторое критическое число электронов должно быть заброшено в зону проводимости, чтобы обеспечить выполнение условия E_fc – Е_fv > E_g. До тех пор пока не будет достигнут этот минимальный уровень инжекции, усиление в полупроводнике не наблюдается.