Теория полупроводникового лазера

Принцип действия полупроводникового лазера можно рассмотреть с помощью рис.6,37, на котором показаны валентная зона полупроводника V зона проводимости С и ширина запрещенной зоны Eg . Если предположить для простоты, что полупроводник Находится при температуре T=0 К, то валентная зона будет полностью заполнена электронами, в то время как зона проводимости будет пуста (см. рис. 1, а, где заштрихованная область является областью заполненных состояний). Предположим теперь, что электроны каким-либо образом переведены из валентной зоны в зону проводимости. Внутри этой зоны электроны за очень короткое время ~ 10^-13 с) перейдут на ее самый нижний уровень, а все электроны вблизи максимума валентной зоны также перейдут на самые нижние из незанятых уровней, так что верхушка валентной зоны будет заполнена «дырками». Отсюда следует, что между валентной зоной и зоной проводимости возникает инверсия населенностей (рис. 6,37,б). Электроны из зоны проводимости сваливаются назад в валентную зону (т. е. они рекомбинируют с дырками), испуская при этом фотон (рекомбинационное излучение). Если между зоной проводимости и валентной зоной существует инверсия населенностей, как показано на рис. 1, б, то процесс вынужденного

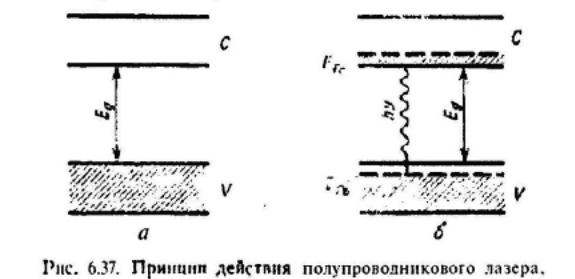
рекомбинационного излучения приведет к генерации при наличии подходящего резонатора и выполнении соответствующих пороговых условий.

Лазерную генерацию на основе вынужденного рекомбинационного излучения в полупроводниковых p-n-переходах наблюдали почти одновременно четыре группы исследователей в 1962 г., причем три из них использовали GaAs.

1. Фотофизические свойства полупроводниковых лазеров

В данном разделе мы напомним некоторые наиболее элементарные результаты теории полупроводников, имеющие непосредственное отношение к нашему обсуждению. За более подробным рассмотрением читатель может обратиться к общепринятым учебникам по квантовой механике твердых тел.

1. Энергетические состояния в полупроводниках

Волновую функцию электрона в данной зоне, например валентной, можно записать в виде волновой функции Блоха:

(6.24)

где обладает теми же свойствами периодичности, что и кристаллическая решетка, а постоянная распространения k связана с импульсом электрона р известным соотношением

(6.25)

Для полупроводникового кристалла, имеющего форму прямоугольного параллелепипеда с размерами L_x , L_y и L_z , вектор k квантуется аналогично выражению (2.10), а именно

(6.26)

где i = х, у, z, а l — целое число.

Если блоховскую волновую функцию (6.24) подставить в волновое уравнение Шрёдингера, описывающее движение электрона в полупроводнике, то окажется, что разрешенные значения энергии электронов Е = Е(к) попадают в зоны, среди которых низшая заполненная зона называется валентной, а следующая, более высокая — зоной проводимости. Появление зонной структуры связано с дифракцией Брэгга блоховской волновой функции на периодическом кристаллическом потенциале. Однако существование валентной зоны и зоны проводимости можно объяснить с помощью несложных физических соображений.

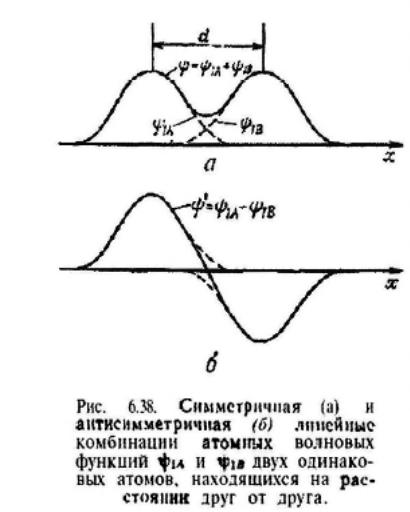
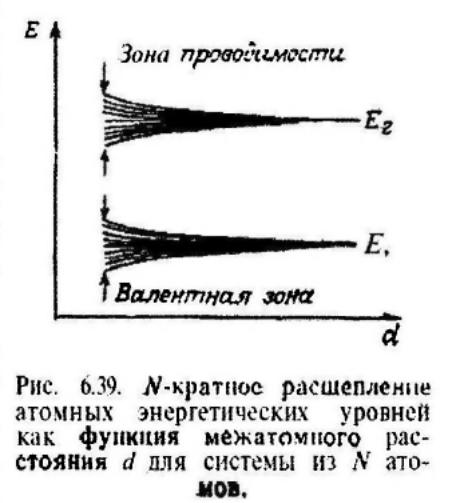
Рассмотрим для простоты случай натрия, в котором каждый атом имеет 11 электронов. Десять из них тесно связаны с ядром и образуют положительный ион с зарядом е. Одиннадцатый электрон движется по орбите вокруг этого иона. Обозначим энергии этого последнего электрона в основном и первом возбужденном состоянии через Е₁ и Е₂, а соответствующие волновые функции ψ₁ и ψ₂. Рассмотрим теперь два атома натрия, расположенные на некотором расстоянии d. Если d много больше размеров атома, то два атома не будут взаимодействовать друг с другом и энергии обоих состояний не изменятся. По-другому это можно выразить следующим образом. Если рассматривать, например, два атома в их энергетических состояниях Е₁ то одноэлектронный уровень энергии двухатомной системы по-прежнему равен Е₁ и этот уровень дважды вырожден. Действительно, полную волновую функцию можно выразить через комбинацию двух волновых функций ψ_1A и ψ_1B, причем эти две функции складываются либо в фазе, либо в противофазе (рис.6,38). В отсутствие потенциала взаимодействия эти два состояния имеют одну и ту же энергию Е₁. Однако когда расстояние между атомами d достаточно мало, энергии этих двух состояний будут слегка различаться: благодаря взаимодействию дважды вырожденный уровень расщепляется на два. Аналогично для системы из N атомов, в которой атомы располагаются достаточно близко друг к другу и взаимодействуют между собой, N -кратно вырожденное состояние с энергией Е₁ расщепляется на N близко расположенных уровней. Следовательно, состояние с энергией Е₁ приводит к валентной зоне, в то время как состояние с энергией Е₂ приводит таким же образом к зоне проводимости (рис. 6,39).

Из предыдущих рассуждений следует, что каждая зона на самом деле состоит из N близко расположенных уровней, где N — полное число атомов в кристалле полупроводника. Поскольку N, как правило, очень велико, отдельные уровни энергии полупроводника внутри каждой зоны в общем случае не могут быть разрешены.

В пределах каждой зоны разрешенные значения энергии можно связать с соответствующими значениями к выражением, которое в приближении параболической зоны записывается так же, как и в случае свободной частицы. Таким образом, для зоны проводимости имеем

где т_с — эффективная масса электрона в зоне проводимости. Аналогично для валентной зоны имеем

здесь т_v (<0)—эффективная масса электрона в валентной зоне. Заметим, что энергия Е отсчитывается от дна зоны проводимости в случае Е_с и от верхушки валентной зоны в случае E_v. На рис.4 построены кривые разрешенных значений Е в зависимости от k, вычисленных по формулам (6.26) — (6.28). На рисунке эти значения обозначены темными точками в валентной зоне и светлыми кружками в зоне проводимости.

Заметим, что, согласно выражению (6.26), разрешенные состояния разделены по оси k равными промежутками 2π/L. Заметим также, что ситуация, изображенная на рис. 6.40, соответствует прямозонному полупроводнику, в котором минимум зоны проводимости и максимум валентной зоны приходятся на одну и ту же точку в пространстве волновых векторов k.