
- •36 § 2. Элементы векторной алгебры
- •Элементы векторной алгебры
- •1. Векторы
- •2. Операции над векторами
- •1 ) Сложение
- •Вычитание
- •Умножение вектора на скаляр :
- •3. Операции над векторами, заданными координатами
- •Сложение:
- •Вычитание:
- •Умножение вектора на число :
- •4. Скалярное произведение двух векторов
- •Свойства скалярного произведения:
- •5. Векторное произведение двух векторов
- •Свойства векторного произведения:
- •6. Смешанное произведение трех векторов
- •Свойства смешанного произведения:
- •7. Примеры с решениями
36 § 2. Элементы векторной алгебры

Элементы векторной алгебры
1. Векторы
О п р е д е л е н и е
1. Вектором
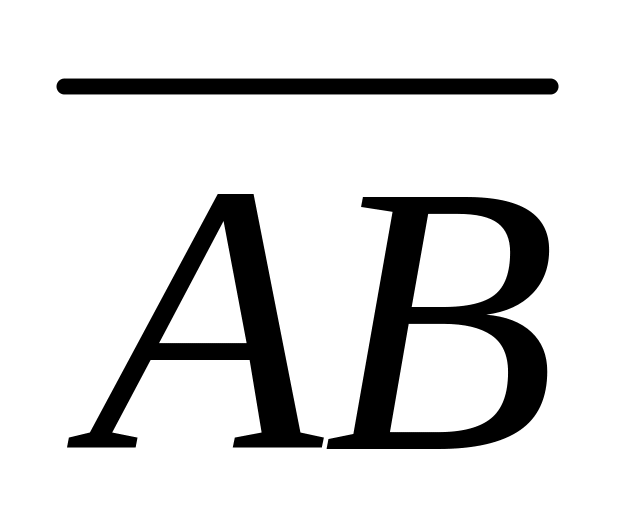 называется направленный отрезок с
началом в точке А
и концом в точке В.
называется направленный отрезок с
началом в точке А
и концом в точке В.
О п р е д е л е н и е 2. Длиной вектора (или модулем) называется длина отрезка АВ. Используют обозначение: | | .
О п р е д е л е н и е
3. Два вектора
![]() и
и
![]() называются
равными,
если они имеют одинаковые длины, лежат
на параллельных прямых (то есть
коллинеарны)
и направлены в одну сторону (то есть
сонаправлены):
называются
равными,
если они имеют одинаковые длины, лежат
на параллельных прямых (то есть
коллинеарны)
и направлены в одну сторону (то есть
сонаправлены):
![]()
О п р е д е л е н и е
4. Проекцией
вектора
на ось
![]() называется число, обозначаемое
называется число, обозначаемое
![]() ,
вычисляемое по формуле:
,
вычисляемое по формуле:


![]() .
.
О п р е д е л е н и е
5. Направляющими
углами вектора
![]() называются углы между ним и координатными
осями:
называются углы между ним и координатными
осями:






![]()
О п р е д е л е н и е 6. Косинусы направляющих углов называются направляющими косинусами вектора.
О п р е д е л е н и е
7. Проекции
вектора
на координатные оси
![]() называются координатами
вектора
и обозначаются, соответственно,
называются координатами
вектора
и обозначаются, соответственно,
![]()
З а м е ч а н и е 1. Для любого вектора верно равенство:
![]() (1)
(1)
где
![]() орты
координатных осей
(то есть единичные векторы, сонаправленные
с соответствующей осью).
орты
координатных осей
(то есть единичные векторы, сонаправленные
с соответствующей осью).
Равенство (1) для сокращения записи заменяют следующим:
![]() .
.
З а м е ч а н и е 2. Для любого вектора верны равенства:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
З а м е ч а н и е 3. У равных векторов равны соответствующие координаты:
![]()
З а м е ч а н и е 4. У коллинеарных векторов координаты пропорциональны:
![]()
![]()
![]()
Причем, если
![]() ,
векторы
и
сонаправлены
,
векторы
и
сонаправлены
![]() ;
если
;
если
![]() ,
векторы
и
противоположно направлены
,
векторы
и
противоположно направлены
![]() .
.
З а м е ч а н и е 5. Длина вектора через координаты определяется по формуле:
![]()
Если известны
координаты точек
![]() и
и
![]() то
то
![]()
![]()
2. Операции над векторами
1 ) Сложение
![]()
![]()

![]() Рис.
1
Рис.
1
Вычитание


![]()

Рис. 2
Умножение вектора на скаляр :


![]()
![]()
![]()


![]()
![]()
Рис. 3
