1.2.Исследование сильно нелинейного уравнения диффузии

Прежде чем исследовать коллоидные системы и создавать их описание, необходимо рассмотреть общее уравнение Лизеганга. Заметим, что исследование сильно нелинейного уравнения вызывает большие сложности. Поэтому исследование этой системы еще находится в начальном периоде и вся работа еще впереди.

Тем не менее, рассмотрим наиболее интересные результаты для простого случая – уравнения (1.1.3). Начнём с построения решения (1.1.3). Система (1.1.3) не полна: нет начальных и краевых условий.

Так как уравнение в системе (1.1.3) имеет первый порядок по времени, то можно ограничиться начальным условием: , где - пространственная координата, - произвольная функция, задающая начальное концентрационное распределение.

Краевое условие связано с поведением геля у стенки. При адсорбции класстеров геля на стенках реактора или электродах необходимо, вообще говоря, указать свою фазовую диаграмму нелинейного уравнения, (или хотя бы свой оператор Лизеганга), которая будет отлична от диаграммы в объёме, так как адсорбция на стекле отличается от кластерной адсорбции макромолекулами осадка. Этот оператор удобно записать в виде связи нормального потока концентрации в направлении стенки сосуда , где - граница, и значения концентрации, в виде системы , где функции - функции, параметризующие «пристеночную» диаграмму, - функция-параметр.

В настоящем разделе ограничимся простым краевым условием постоянной адсорбции кластеров на стенке: .

Таким образом, задача (1.1.3) с краевыми и начальными условиями (без учёта пристеночного оператора) примет вид:

(1.2.1)

Рассмотрим задачу в простейшем случае, то есть задачу на отрезке . Для этого случая задача (1.2.1) примет вид:

. (1.2.2)

Дифференциальное уравнение задачи относится к виду сильно нелинейных уравнений, и даже в самом простом случае эта задача не имеет единственного решения.

Рассмотрим теоремы единственности и существования решения этой задачи.

Верен следующий набор утверждений, представленный в Abstract 1.1:

Abstract 1.1

Теорема 1. Для всяких и для всяких , выполнено: .

Доказательство: Проводится непосредственной проверкой.

Теорема 2. Пусть дана система

Пусть решение этой системы существует. Тогда оно удовлетворяет формуле [1]: .

Доказательство: Будем рассматривать как некую неизвестную функцию , а - как произвольную функцию . Тогда согласно [9] они связаны соотношением .

Теорема 3. Пусть - мало (эта оценка выполнена при ). Тогда решение задачи может быть оценено как для всех .

Доказательство: Согласно доказанному выше .

Заметим, что каким бы ни было , всегда заключён в пределах от -1 до +1. Следовательно, . Внутренние интегралы вычисляются, и не превышают 1, а, следовательно, выполнена оценка: . А так как , то для выполнена более жёсткая оценка: . И, следовательно, . Вычисляя арксинус, получим оценку теоремы.

Теорема 4. Пусть . Пусть существует хотя бы одно решение задачи

Тогда оно единственно.

Доказательство: Предположим, что существуют два различных решения: и . Тогда каждое из них удовлетворяет уравнению: , с однородными начальными и краевыми условиями. Вычтем эти уравнения друг из друга, проведём преобразования разностей тригонометрических функций и введём обозначения: , . Получим: . Теперь обозначим . Получаем: .

Умножим обе части уравнения на и проинтегрируем по от 0 до , а по - от нуля до бесконечности. После преобразований [9] получим: . По доказанным выше оценкам решений и , . Следовательно, правая часть отрицательна, а левая – неотрицательна. Равны они могут быть лишь если выражение слева и справа равны нулю. Отсюда следует, что решения и совпадают.

Теперь решим вопрос о существовании решения дифференциального уравнения.

Теорема 5. Решение задачи существует и единственно.

Доказательство: можно найти в [10].

Теорема 6. Решение задачи

существует, единственно и может быть найдено по формулам итерационного процесса (см. доказательство).

Доказательство: Покажем, что решение задачи существует. Воспользуемся формулой теоремы 2, получим

. Покажем, что решение этого интегрального уравнения может быть построено при небольших с помощью итераций: , тогда , . Покажем, что итерационный процесс сходится при определённых значениях . Для этого составим разность и , которую обозначим . Вычитая формулы и упрощая выражение, получим: . В том случае, если , получаем оценку: , где . Эта последовательность сходится к нулю, т.е. последовательность итераций фундаментальна, а, следовательно, сходится.

Замечание. Отметим, что точно так же (вычитая из точного решения) можно показать, что эта последовательность итераций сходится к точному решению. Единственность решения можно доказать способом, сходным со способом доказательства теоремы 4.

Теорема 7.

Итерационный процесс сходится к точному решению задачи при .

Доказательство: Вычтем из точного решения результат, полученный на -ом шаге. .

Введём , тогда получаем: . Отсюда мы получаем, учитывая оценку теоремы 3, что , где для всех . Следовательно, последовательность сходится к нулю.

Сходным образом можно доказать аналогичные теоремы для , удовлетворяющему уравнению , для и т.д. – для всякого .

Покажем, что является сходящейся, и сходится она к точному решению задачи при . Действительно, покажем, что последовательность сходится. Для этого вычтем из точного решения величину . Получим , где , , и остаток ряда . Остатки рядов и можно оценить как , где и - числа, по модулю не превосходящие 1. Учитывая оценку, получим, что остатки рядов не превышают , где - некое число. Следовательно, правая часть стремится к нулю при . Разрешая уравнение для итерациями и учитывая, что последовательность может быть оценена сверху как геометрическая прогрессия со знаменателем, меньшем единицы по модулю, получим: . Получим: . Эта последовательность является сходящейся к нулю, что и доказывает теорему.

Как следует из доказанного в Abstract 1.1, ничего нельзя сказать про случай, когда решение составляет . Возможно, что в этом случае решений больше одного, а возможно – решений нет вовсе, и необходимо строить квазирешение.

Численные методы, тем не менее, позволяют построить «решение», которое выглядит следующим образом, рис.1.3.

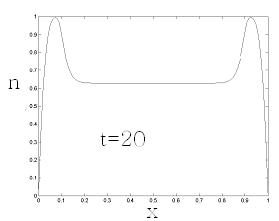
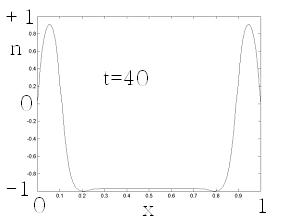
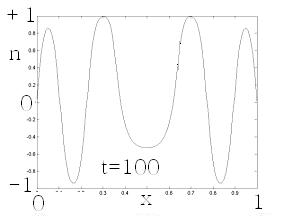
Рис.1.3.

Численное решение задачи 1. 1.3 для разных моментов времени (распределение концентрации по координате в зависимости от времени). Верхний рисунок слева – для 20-го момента времени, верхний справа – для момента 40, снизу слева – 80, снизу справа – 100. время безразмерное, диффузия принята равной единице.

Таким образом, получено дифференциальное уравнение, отнесённое к фазовой диаграмме (рис.1.2). Однако из работ [11,12] следует, что рассматриваемое решение во времени является колебательным, но совсем необязательно – периодическим. Следовательно, фазовая диаграмма рис. 5.3 может быть замкнутой кривой или даже кривой неограниченной длины, располагающейся в некоторой ограниченной области замкнутого пространства.

Abstract 1.2.

Стационарная задачу формирования геля.

Гелевые кластеры формируют сложную структурную организацию, которую можно измерить. При неограниченном увеличении времени решение дифференциального уравнения будет стремиться к стационарному решению (если таковое есть). Поэтому удобно построить решение и в стационарном случае – с тем, чтобы сравнить его с экспериментальными данными.

Для этого необходимо получить из (1.2.2) стационарную задачу.

(1)

Так как ищем стационарное решение, то производную по времени в этом соотношении можно положить равной нулю:

(2)

Эту систему удобно переписать, используя замену: . Тогда, в зависимости от величины , или . Масштабируя переменную ( ), и переобозначая на , получим краевую задачу:

(3)

(оператор Лизеганга в этом случае может быть переписан как ). Решение этой задачи представляет определённую сложность: - особая точка фазовой диаграммы, и решение уравнения может быть в этой точке не единственно. В этой точке знак корня можно сменить и, таким образом, получить решение дифференциального уравнения в области определения.

Рассмотрим следующую краевую задачу:

(4)

где - некоторое число, которое нам неизвестно. Мы будем его подбирать из таких соображений, чтобы решение на интервале было единственным.

Покажем, что это возможно. Понизим порядок дифференциального уравнения. В результате получим соотношение: , где - произвольная постоянная. Подставим это соотношение в краевые условия задачи: , . В результате имеем уравнение для нахождения : . Следовательно, . Исходя из условия , выберем знак .

Таким образом, . Согласно [1-Эльсгольц], уравнение первого порядка имеет особую точку при тех значениях , при которых . Выясним, при каких значениях это возможно.

Дифференцируем , получаем: . Знаменатель будет отличено от нуля при всяком , и равен нулю при . Вычисляя предел , получим, что он стремится к бесконечности. Итак, особая точка – только .

Выясним, будет ли решение уравнения существовать. Отметим, что условие выполняется, если . Заметим, что решение уравнения при будет возрастающей функцией по . Оно достигнет при некотором конечном значения - то есть своей особой точки . Обозначим это значение , при всяком . Заметим, что в силу единственности решения при всяком решение будет также единственно и в .

Будем искать решение в виде ряда. Для этого нам удобно перенести нуль в особую точку, введя переменную . Переобозначим , и в результате получим задачу

(5)

Решение необходимо искать в виде ряда по степеням , кратным , т.е. . Удобно для дальнейших вычислений ввести также выражение . Коэффициенты и связаны соотношениями:

(6)

Коэффициенты ряда следует искать, дифференцируя выражение . В результате получим набор рекуррентных соотношений для коэффициентов и :

(7)

Необходимо показать, что коэффициенты растут не слишком быстро, и, следовательно, ряд является сходящимся. Для этого будем рассматривать каждый из рядов по отдельности. Рассмотрим первое из слагаемых формулы для :

Выберем из коэффициентов самый большой, обозначим его за . Заменим знаки минус на плюс, от этого выражение не уменьшится. Несложно видеть, что этот ряд представляет собой часть разложения в ряд для . Сходным образом можно оценить и все остальные ряды: для следующего это будет и т.д. Оценивая и эти ряды, получим для выражения в скобках . Следовательно, . В том случае, если зависит от (например, ), получаем , и ряд сходится при всяком . В том случае, если ряд начинается наибольшим из коэффициентов с некоторого номера, то этот ряд коэффициентов довольно быстро убывает и оказывается сходящимся рядом. В этом случае ряд сходится, по крайней мере в радиусе . При больших эта оценка не является состоятельной, но, скорей всего, выполнена ещё более сильная оценка.