1.2. Биения

Биения – это результат сложения двух «однонаправленных» синусоидальных колебаний с неравными, но близкими частотами:

, (5)

, (6)

где ω₂ немного больше ω₁, так что Δω=ω₂−ω₁≪ω₁ и ω₂. Начальные фазы в (5) и (6) взяты нулевыми, так как в результат сложения они входят несущественным образом, но сильно загромождают его. Для выделения существа результата взяты одинаковыми и амплитуды колебаний.

Так как метод векторных диаграмм предназначен только для операций с синусоидальными величинами одинаковых частот, то здесь он не применим. Для сложения (5) и (6) используем известную формулу тригонометрии 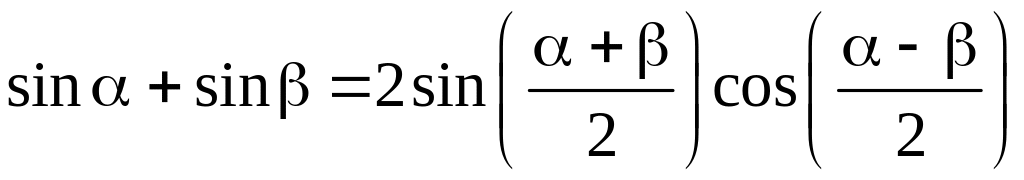; это даёт:

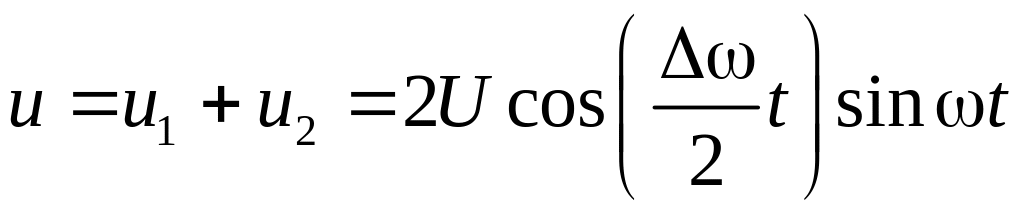, (7)

г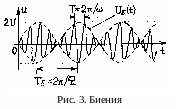 де Δω=ω₂−ω₁, ω=(ω₁+ω₂)/2≈ω₁≈ω₂.

Функция (7) описывает биения – «быстрые» колебания sin ωt с медленно меняющейся амплитудой

U_б(t)= .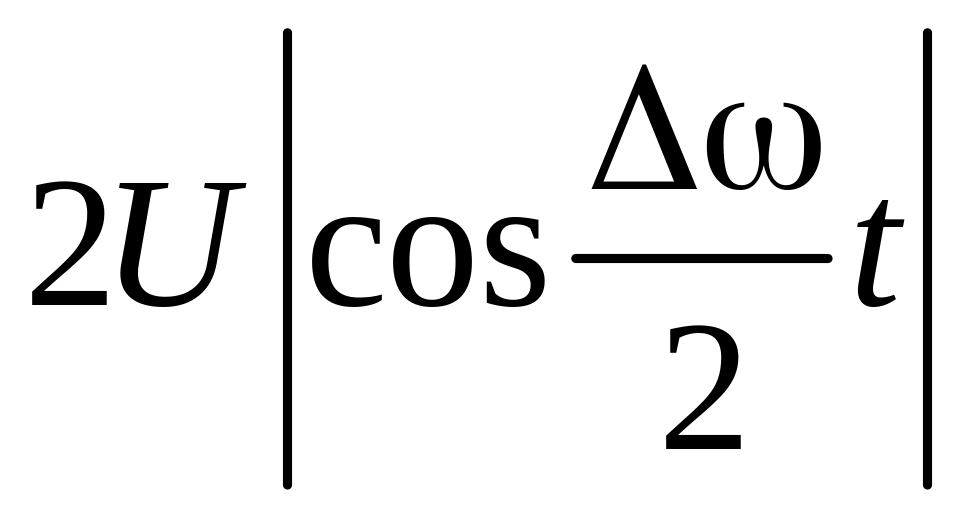

Частота Ω=Δω называется угловой частотой биений; Т_б=2π/Ω − период биений (рис. 3).

1.3. Сложение взаимно перпендикулярных колебаний

с одинаковыми частотами

Пусть точка участвует одновременно в двух взаимно перпендикулярных синусоидальных колебаниях по осям х и у с одинаковыми частотами:

, (8)

, (9)

где Х и Y – амплитуды колебаний, φ – сдвиг фаз между ними. Функции (8) и (9) задают траекторию результирующего движения точки в параметрической форме. Чтобы получить уравнение траектории в координатной форме f(x, y)=0, надо объединить (8) и (9), избавившись от параметра t. Сделаем это.

Из (8) имеем:

.

А так как

,

то (9) даёт:

,

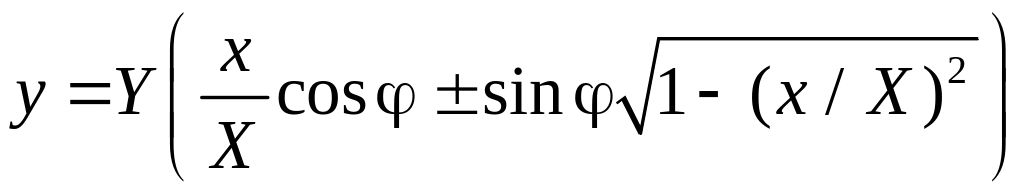или

.

П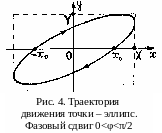 осле возведения последнего уравнения в квадрат и несложных преобразований получаем:

. (10)

Это уравнение эллипса, оси которого повёрнуты относительно осей х и y на некоторый угол (рис. 4).

Замечание. Фазовый сдвиг φ в (10) – это не угол поворота эллипса на рис. 4.

При φ=±π/2 эллипс (10) приводится к координатным осям:

,

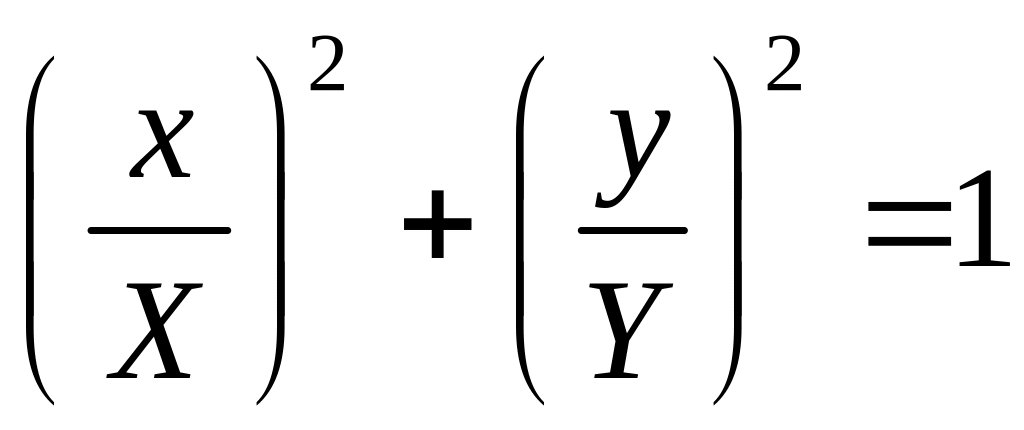а при φ=±π/2 и Y=Х он вырождается в окружность. При φ=0 или φ=π эллипс вырождается в прямой отрезок у=±kx, где k=Y/Х.

Таким образом. точка, колеблющаяся по осям х и у по законам (8) и (9), в результате описывает в плоскости (х, у) траекторию эллипса (10). Этот эллипс всегда вписан в прямоугольник (2Y×2Х), а его ориентация в этом прямоугольнике определяется фазовым сдвигом φ: при |φ|<π/2 эллипс вытянут в направлении квадрантов 1-3, как показано на рис. 4, а при π/2<|φ|<π он вытянут в направлении квадрантов 2-4.

Для наблюдения эллиптической траектории на экране осциллографа на пластины Х его трубки подают напряжение (8), а на пластины Y − напряжение (9). Эти напряжения снимаются с каких-либо участков цепи с активными и реактивными элементами, питаемой от одного генератора с частотой ω. В качестве такой цепи можно взять, например, последовательную RC-цепочку, изображённую на рис. 1, и подавать на входы Х и Y осциллографа любую пару напряжений из трёх: и_R, и_С, и. Если эллипс (10) на экране расположить строго симметрично относительно начала координат, то по точкам его пересечения с осями х или у можно определить фазовый сдвиг φ между напряжениями (8) и (9). Действительно, полагая в (10) у=0, получим для точек ±х₀ пересечения эллипсом оси х (рис. 4):

,

откуда

, (11)

причём это отношение не зависит от коэффициента усиления осциллографа по каналам Х и Y.^)