1.6.3. Режим смешанных волн

Если линия нагружена на сопротивление Z_н, не равное 0, ∞, jX_н или ρ, то в ней устанавливается режим смешанных волн, когда в линии существуют отражённые волны, но меньшей амплитуды, чем падающие, поскольку часть энергии поглощается активной компонентой нагрузки. Ограничимся рассмотрением варианта чисто активной нагрузки, когда Z_н=R_н≠ρ.

Как видно из (22), при Z_н=R_н коэффициент отражения

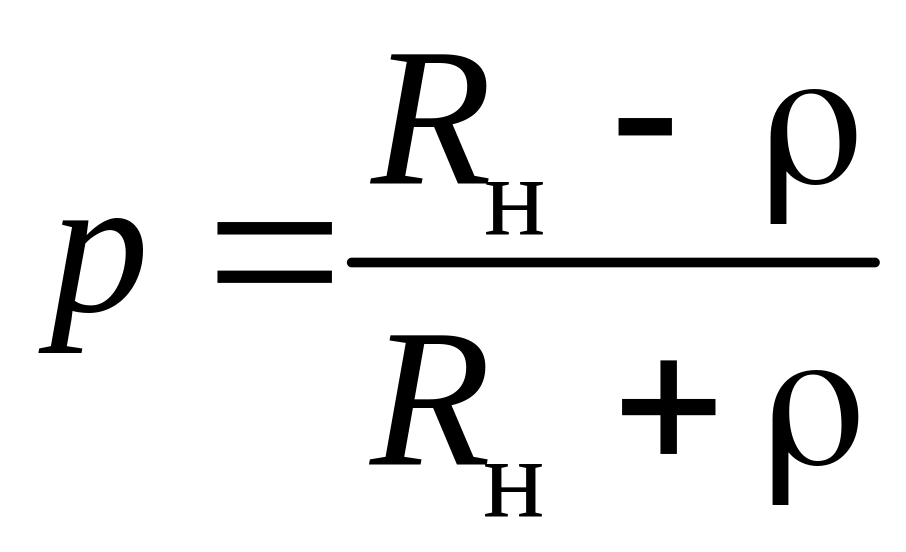. (27)

Уравнения (17) принимают вид:

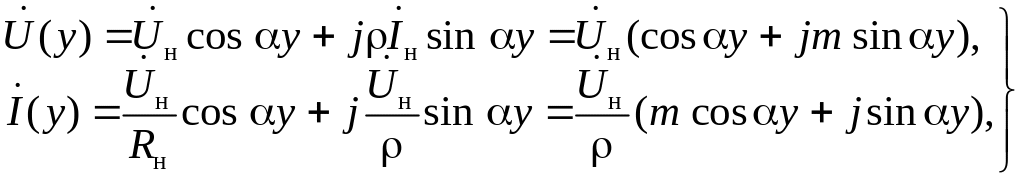
где m=ρ/R_н. Отсюда для действительных амплитуд получаем:

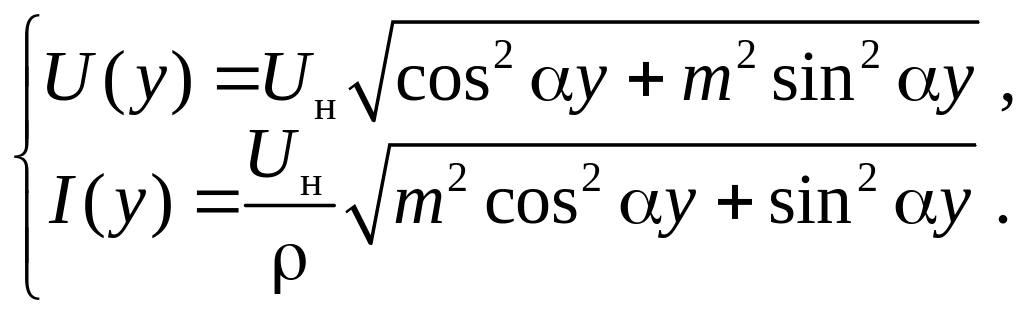
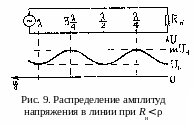
На рис. 9 в качестве примера показан график U(y) при m>1, т.е. при R_н<ρ.

Смешанную волну можно представить в виде суперпозиции бегущей и стоячей волн.

1.7. Коэффициент стоячей волны

Режим работы линии можно характеризовать коэффициентом отражения , определяемым формулой (21). Однако разделить падающие и отражённые волны для измерения их амплитуд практически трудно, поэтому для количественной оценки режима работы линии вводится другая величина, связанная с коэффициентом отражения, но легко измеряемая. Эта величина называется коэффициентом стоячей волны (КСВ) и определяется как отношение максимальной и минимальной амплитуд напряжения (или тока) в линии^):

КСВ=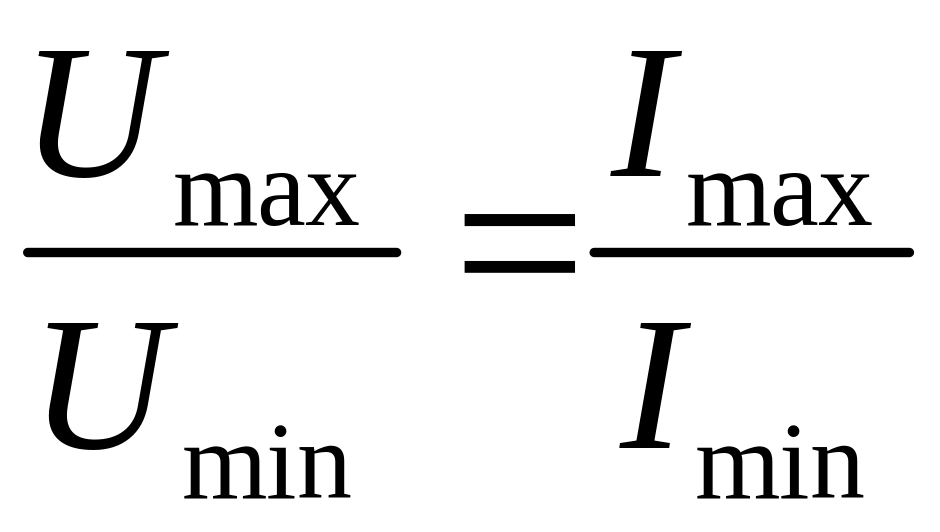 . (28)

Из этого определения следует, что

● в режиме бегущих волн, т.е. при Z_н=ρ: КСВ=1;

● в режиме стоячих волн, т.е. при Z_н=0, ∞ или jХ_н: КСВ=∞;

● в режиме смешанных волн, т.е. при Z_н=R_н+jХ_н: 1<КСВ<∞.

Из определения (28) легко установить связь КСВ и коэффициента отражения. В сечении линии. где U=U_max, падающая и отражённая волны складываются в фазе, а где U=U_min – в противофазе, поэтому можно записать:

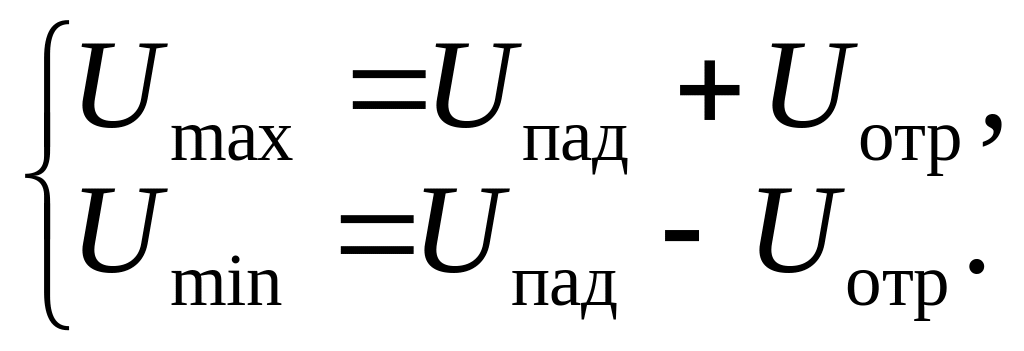
Отсюда

КСВ= = ,

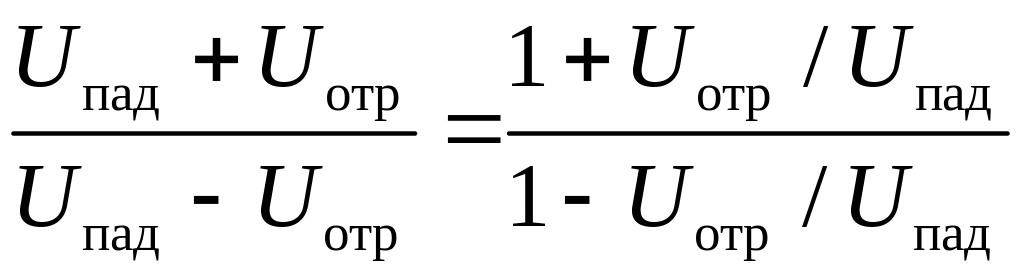или, с учётом (21),

КСВ= , (29)

. (30)

Чем ближе КСВ к единице, тем лучше согласование нагрузки с линией. Согласование считается

● хорошим, если КСВ≤1,5 (при этом р≤0,2),

● удовлетворительным, если 1,5<КСВ≤3 (0,2<р≤0,5),

● плохим, если КСВ>3 (р>0,5).

Из (27) и (29) следует. что при чисто активной нагрузке Z_н=R_н

КСВ= (31)

Поскольку основным назначением передающей линии является передача максимальной мощности от генератора к потребителю (к нагрузке), то важно уметь выражать КСВ через падающую и отражённую от нагрузки мощности. Так как мощность Р~U², то из (21) и (30) получаем долю отражённой мощности:

.

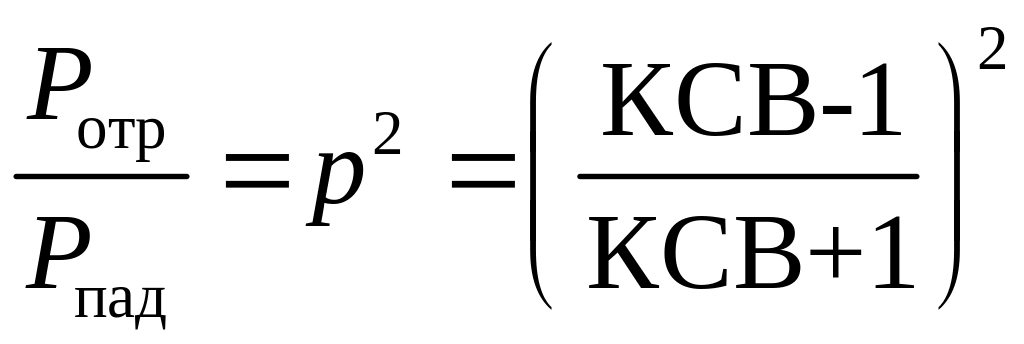Таким образом, при хорошем согласовании, когда КСВ≤1,5, отношение 4%, а при удовлетворительном – 25%.

2. Эксперимент

2.1. Предварительные расчёты

При домашней подготовке к работе выполнить следующее.

1. По заданной поперечной геометрии линии (см. разд. 2.3) вычислить по формулам (18) её погонные параметры L₀ (мкГн/м) и С₀ (пФ/м), а по формуле (19) – её волновое сопротивление ρ.

2. Воздушную линию можно считать без потерь, если её погонное сопротивление R₀≪ωL₀. С учётом скин-эффекта, погонное сопротивление цилиндрического провода радиусом r на частоте f оценивается по формуле

R₀= ,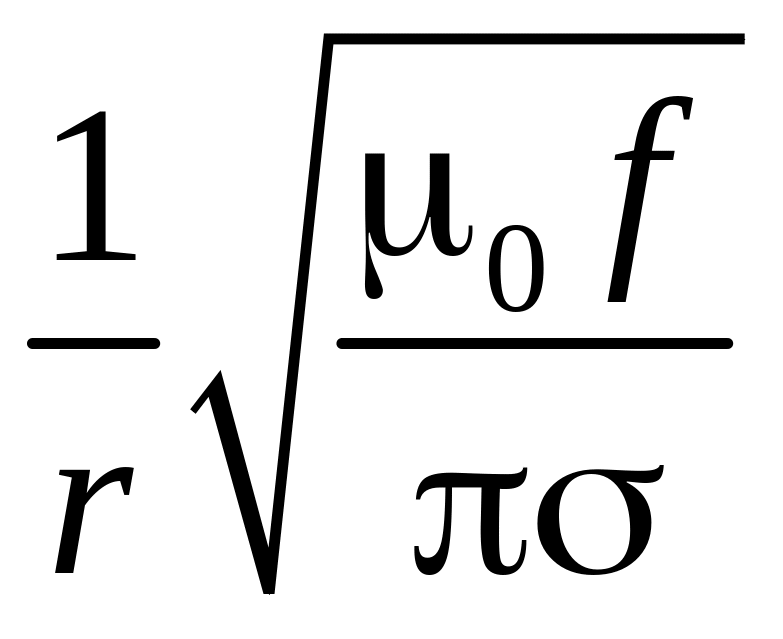

где σ – проводимость материала провода.

Оценить, выполняется ли условие R₀≪ωL₀ на частоте f=100 МГц.