1.5. Вторичные параметры линии без потерь

Вторичными называются параметры, выражаемые через первичные – погонные величины R₀, L₀, C₀ и G₀ и импеданс нагрузки Z_н. Для линии без потерь R₀=0 и G₀=0. Ко вторичным параметрам относятся: волновое сопротивление, входное сопротивление, коэффициент отражения, волновое число и фазовая скорость.

1.5.1. Волновое сопротивление

Определение волнового сопротивления было дано в разделе 1.4, а его выражение через первичные параметры – формулой (15):

ρ= .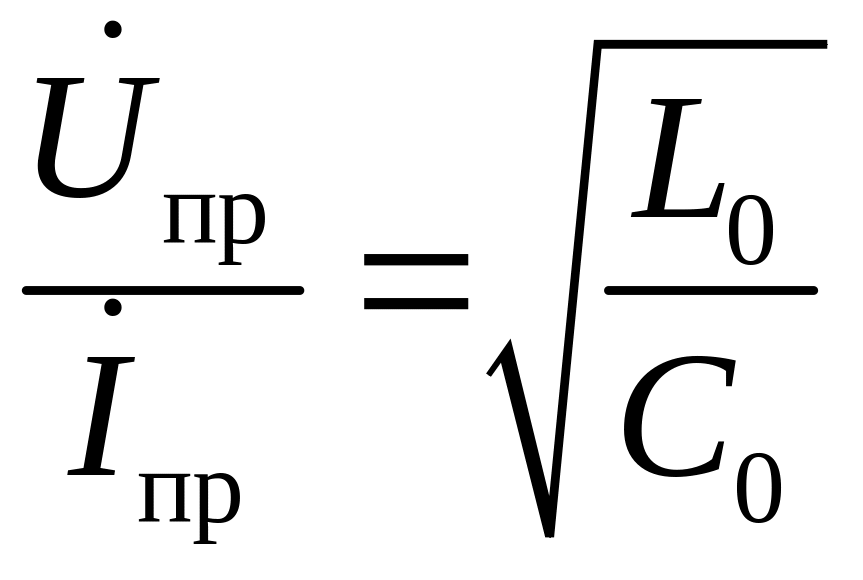

Видно, что волновое сопротивление линии без потерь является действительным числом и не зависит от частоты.

Известно, что погонные индуктивность и ёмкость двухпроводной линии, показанной на рис. 1, в приближении r≪d следующие:

L₀= , С₀= , (18)

где ε₀ и μ₀ – электрическая и магнитная постоянные. Следовательно, волновое сопротивление двухпроводной линии

ρ=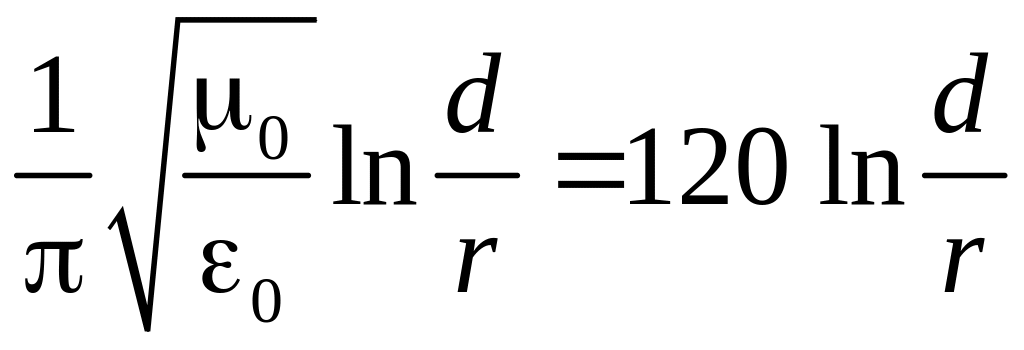 [Ом]. (19)

Так как обычно отношение d/r~10…100, то волновое сопротивление такой линии имеет порядок нескольких сотен ом.

1.5.2. Входное сопротивление

Определение. Отношение комплексных амплитуд напряжения и тока в данном сечении линии называется входным сопротивлением линии в этом сечении:

Z_вх= .

Подставляя сюда и из (17), получаем для входного сопротивления линии в данном сечении у:

Z_вх=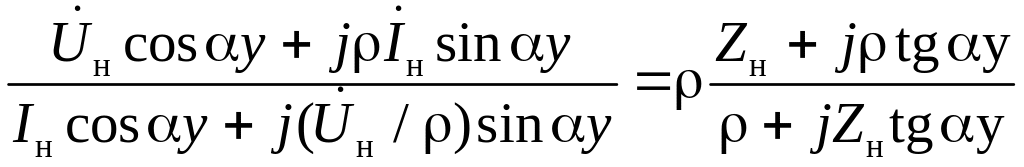 , (20)

где

Z_н=

− импеданс нагрузки. Таким образом, входное сопротивление является, вообще говоря, числом комплексным, причём Z_вх=Z_вх(ρ, Z_н, ω, у), а на конце линии (при у=0) Z_вх=Z_н.

1.5.3. Коэффициент отражения

Волны токов и напряжений, возбуждаемые в линии генератором, доходят до нагрузки Z_н и, вообще говоря, частично или полностью отражаются от неё обратно в линию, так что коэффициент в (13а) и (13б), соответствующий комплексной амплитуде отражённых волн, в общем случае не равен нулю.

Определение. Отношение комплексных амплитуд напряжений (или токов) отражённой и падающей волн в некотором сечении линии называется коэффициентом отражения в этом сечении:

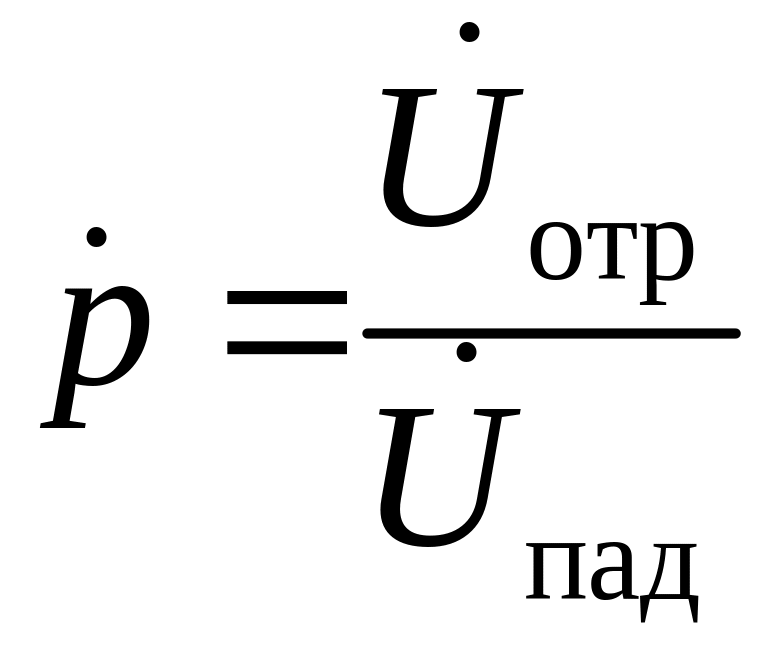. (21)

Из (13а) и (16) имеем:

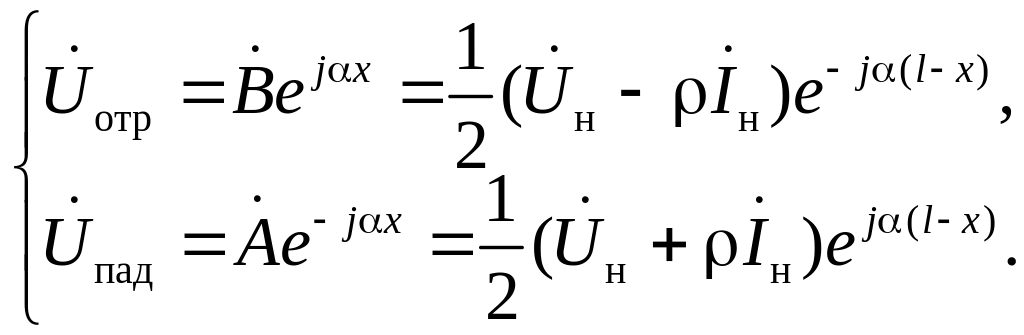
Тогда

.

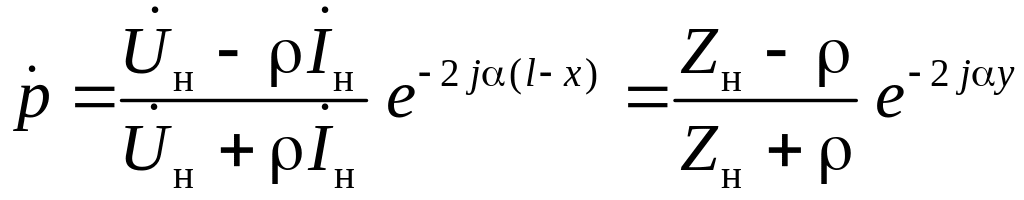Обычно представляет интерес не сам коэффициент отражения, а его модуль, поэтому далее везде под коэффициентом отражения будем понимать величину

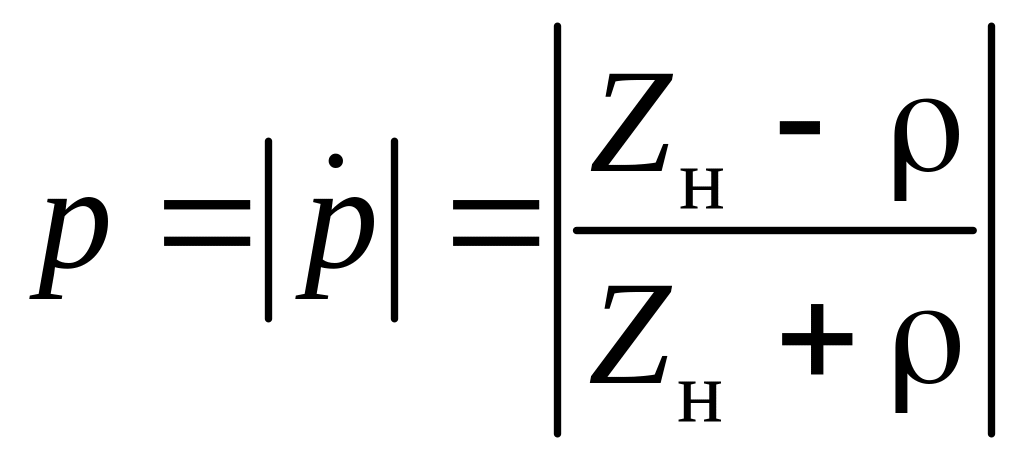. (22)

Видно, что всегда 0≤р≤1. Действительно, пусть Z_н=R_н+jX_н, тогда

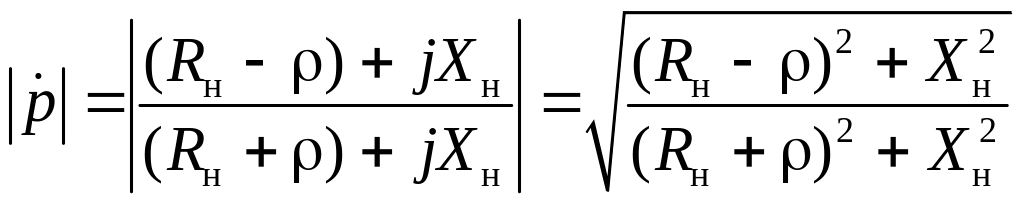≤1. (23)

1.5.4. Волновое число и фазовая скорость

Рассмотрим аргумент синуса (ωt−αх) в формуле (14), который называется фазой волны. Если число ω характеризует скорость изменения фазы в данном сечении линии х, то число α − «скорость» изменения фазы вдоль линии в данный момент t. Это число α называется волновым числом. Оно «произошло» из уравнения (11) и выражается через погонные параметры линии и частоту ω формулой (12)

.

Определение. Фазовой скоростью υ волны называется скорость перемещения вдоль линии неизменного фазового состояния, т.е. какой-либо фиксированной фазы напряжения или тока.

Выразим фазовую скорость через другие параметры линии. Для этого запишем условие постоянства фазы: (ωt−αх)=const. Дифференцируя это по времени и учитывая (12), получаем:

υ= ,

что совпадает с (7). Подстановка сюда выражений (18) даёт численное значение фазовой скорости волн в двухпроводной линии:

υ= 3·10⁸ м/с.

Таким образом, вóлны токов и напряжений бегут по линии без потерь со скоростью света в вакууме.

Определение. Расстояние λ, которое волна пробегает за период Т, называется длиной волны:

λ=υT= . (24)

Полагая υ=с, Т=1/f, получаем: λ=с/f, где f – частота генератора.