1.2. Метод узловых потенциалов
З
а
неизвестные в этом методе принимаются
потенциалы
узлов
φk.
Если мы узнаем потенциалы всех узлов
цепи, то затем уже легко сможем определить
ток в любой ветви между узлами «k»
и «n»
из обобщённого закона Ома:
iR=+(φk−φn) (3)
(знаки слагаемых здесь соответствуют стрелкам тока и ЭДС на рис. 3).
Пусть цепь имеет N узлов. Один узел мы всегда можем заземлить, положив его потенциал φ=0. Следовательно, неизвестными в этом методе остаются (N−1) величин φk. Значит, метод узловых потенциалов приводит всего лишь к (N−1) алгебраическим уравнениям, т.е. сколько даёт лишь 1-е правило Кирхгофа.
Р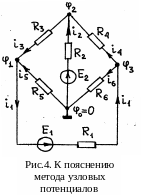
ассмотрим
работу этого метода на примере цепи,
показной на рис. 4 (мостовая схема). Она
имеет четыре узла и три независимых
контура. Прямое использование правил
Кирхгофа привело бы здесь к 3+3=6 уравнениям
относительно неизвестных токов в ветвях.
Метод узловых потенциалов приводит
лишь к трём уравнениям.
Заземлим, например, узел 0, положив φ0=0, и определим потенциалы узлов φ1, φ2 и φ3. Расставим произвольно стрелки токов ik в ветвях (k=1, 2, …,6) и запишем первые уравнения Кирхгофа для узлов 1, 2 и 3:
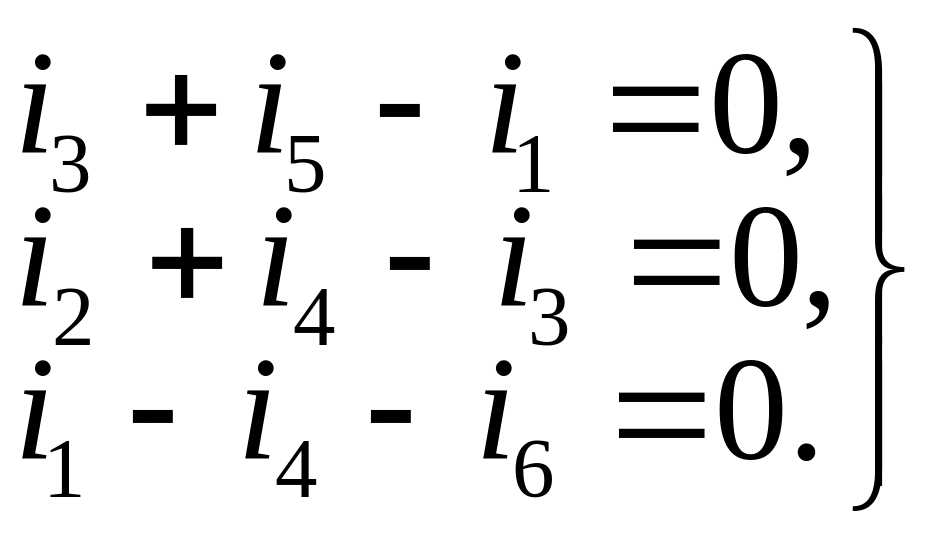(4)
Теперь выразим эти токи из обобщённого закона Ома (3) с учётом правила знаков:
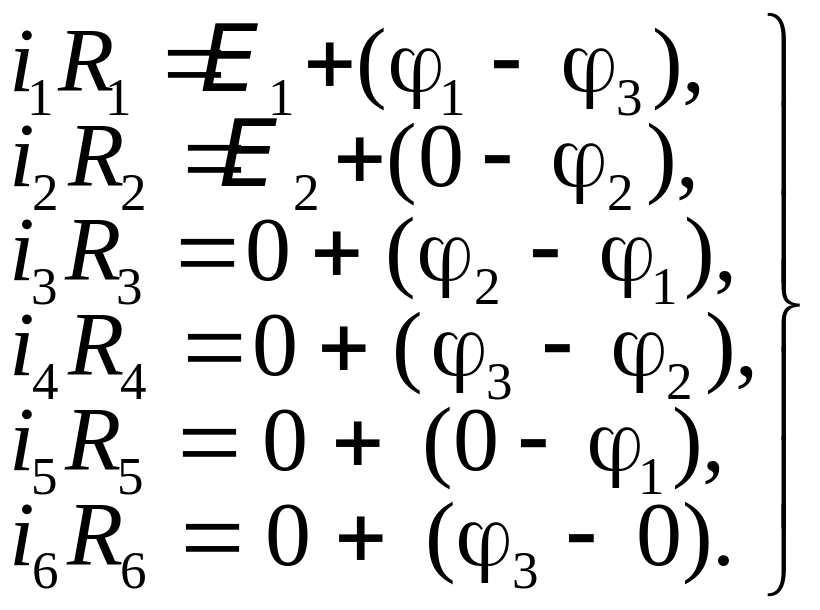(5)
Подставив найденные отсюда i1, i2, …, i6 в (4), получим систему трёх уравнений относительно неизвестных потенциалов φ1, φ2 и φ3:
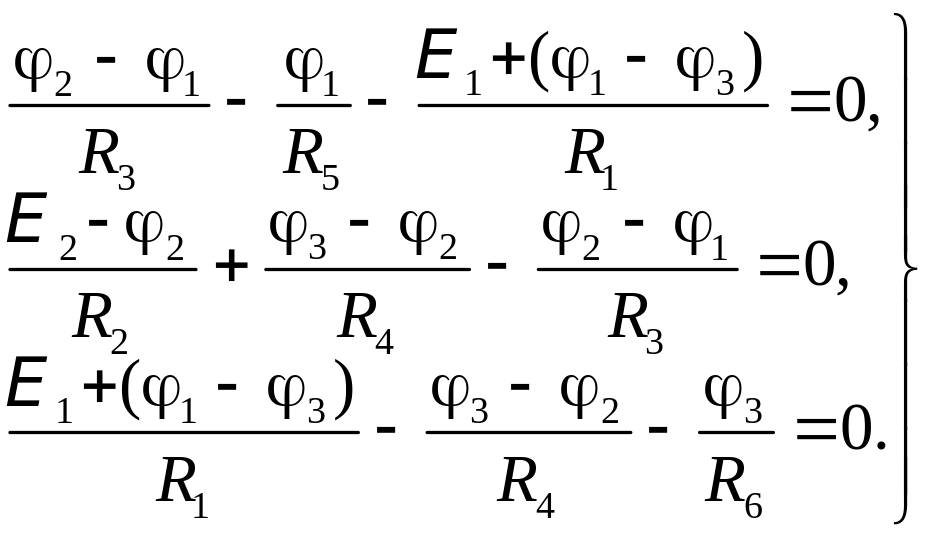
Определив из этой системы потенциалы узлов φ1, φ2 и φ3, и подставив их в (5), находим все токи i1, i2, …, i6 с их знаками относительно выбранных на рис. 4 стрелок.
1.3. Метод контурных токов
Если цепь имеет N узлов и К независимых контуров, то для расчёта токов на всех участках такой цепи правила Кирхгофа дают (N−1)+К уравнений. Метод узловых потенциалов позволяет обойтись системой лишь (N−1) уравнений, т.е. сколько даёт первое правило Кирхгофа. Метод же контурных токов приводит к К уравнениям, т.е. к стольким, сколько даёт второе правило Кирхгофа. Этот метод состоит в следующем.
П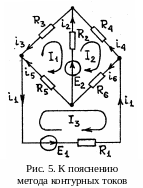
усть
цепь имеет К
независимых контуров. Каждому из них
ставится в соответствие некоторый ток
In
(n=1,
2, …,К),
постоянный вдоль всего контура. Такие
токи называются контурными.
Удобно все контурные токи направлять
одинаково, скажем, по часовой стрелке.
Рассмотрим, для определённости, ту же
мостовую схему, что и на рис. 4. Она имеет
три независимых контура (выберем их
простыми), следовательно, в ней задаются
три контурных
тока:
I1,
I2,
I3
(рис. 5). При одинаковом направлении
контурных токов, истинные
токи
в смежных ветвях (i2,
i5
и i6)
будут равны разностям двух соседних
контурных токов, а в ветвях, не являющихся
смежными, истинные
токи
(i1,
i3
и i4)
будут совпадать с контурными.
Для изображённой на рис. 5 схемы второе правило Кирхгофа для контурных токов даёт:
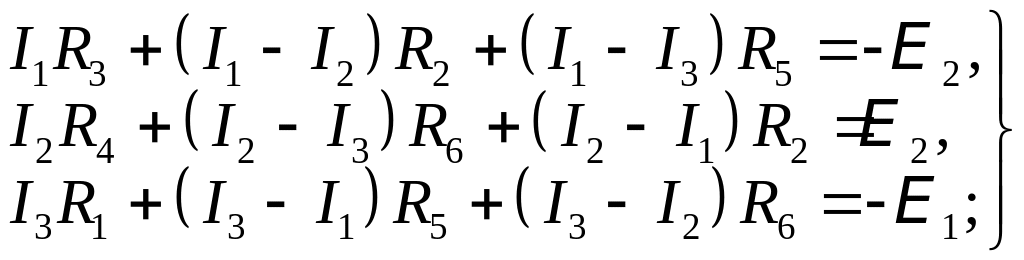
или:
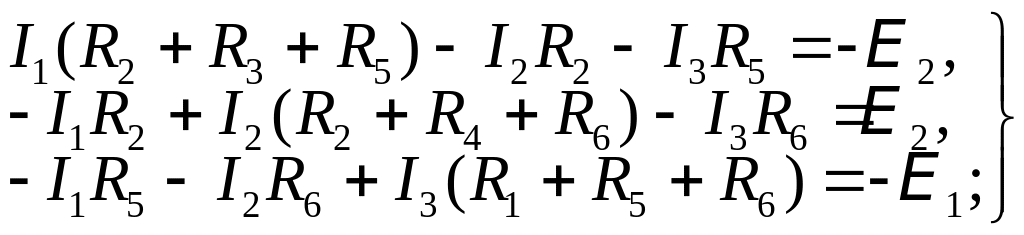
Решая эту систему уравнений, получим три неизвестных контурных тока : I1, I2 и I3. Затем определяем истинные токи в ветвях с их знаками относительно выбранных стрелок:
i1=−I3, i2=I2−I1, i3=−I1, i4=−I2, i5=I1−I3, i6=I2−I3.
Следует отметить, что в методе контурных токов первое правило Кирхгофа выполняется автоматически, в силу самой идеи метода. Действительно, например, для представленной на рис. 5 схемы:
______________________________________
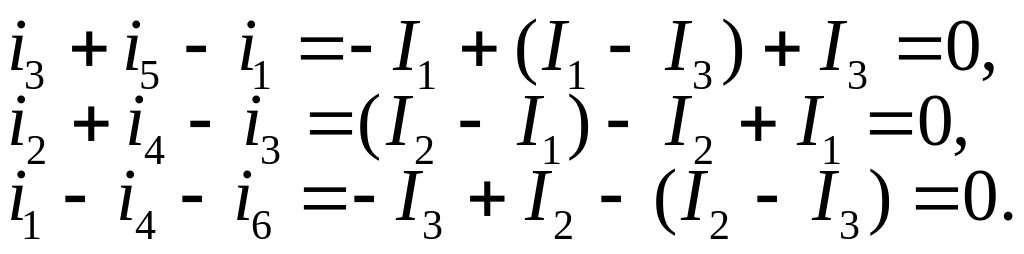
В
ыбор
того или иного метода расчёта зависит
от конкретного графа
(сетки) электрической цепи: если граф
таков, что в нём много контуров, но мало
узлов, то удобно пользоваться методом
узловых потенциалов, в противном случае
– методом контурных токов. Так например,
для цепи, изображённой на рис. 2, метод
контурных токов даёт два уравнения, а
метод узловых потенциалов – всего одно:
относительно потенциала верхнего узла
при заземлённом нижнем.
2. ЭКСПЕРИМЕТАЛЬНАЯ УСТАНОВКА
Рабочая установка представляет собою настольный стенд, в котором смонтирована цепь, изображённая на рис. 6.
К двум парам гнёзд этой цепи могут подключаться либо внешние генераторы постоянного напряжения 1 и 2, либо короткозамыкающие перемычки. Резистор R4 – подстроечный, его сопротивление в лабораторной установке может отличаться от 557 Ом.
Напряжения на всех элементах цепи измеряются цифровым вольтметром с точностью до трёх знаков.