1.2. Действие магнитного поля на ток (сила Ампера)

Так как магнитное поле действует на отдельные движущиеся заряды, то оно будет действовать и на ток, представляющий собою упорядоченное движение свободных зарядов в проводнике.

П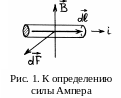 усть в магнитном поле В находится цилиндрический провод с током i. Вырежем из провода малый элемент dl, объем которого dV=Sdl, где S – сечение провода. В этом объеме находится свободный заряд dq=e dN=endV, движущийся с дрейфовой скоростью υ (здесь е – заряд свободного носителя, n – концентрация носителей). Следовательно, на этот элемент провода действует сила Лоренца dF=dq(v×B)=(nev×B)Sdl. А так как nev=j – плотность тока, jS=i – ток в проводе, то, обозначая ориентированный элемент провода вектором dl (dl↑↑j) , можно записать

d F=i (d l×B). (2)

Эта сила называется силой Ампера; она перпендикулярна как элементу dl, так и вектору В на данном элементе (рис. 1).

1.3. Закон Био-Савара

Опыт показывает, что магнитное поле не только действует на движущиеся заряды, но и само порождается движущимися зарядами (токами). На основе обобщения экспериментальных данных установлено, что если по тонкому проводу идет ток i, то каждый элемент dl этого провода создает в пространстве магнитное поле

d B= , (3)

где r – радиус-вектор, проведенный от элемента dl к точке М, где измеряется магнитное поле (рис. 2), k – коэффициент пропорциональности, зависящий от выбора системы единиц. В системе СИ, где единицей магнитного поля является тесла (Тл), коэффициент k= . Величина обозначается символом μ₀ и называется магнитной постоянной: μ₀= =4π·10⁻⁷ Гн/м. Таким образом, в системе СИ закон Био-Савара имеет вид

dB= . (4)

Замечание. Часто в качестве закона Био-Савара принимается иная, но эквивалентная (4) форма записи:

B= , (5)

где В – магнитное поле, создаваемое точечным зарядом q, движущимся в выбранной системе отсчета со скоростью v, r – радиус-вектор, проведённый из заряда q в точку наблюдения М. Из формулы (5) легко получить (4) по процедуре, описанной в разд. 1.2.

Как показывает опыт, для поля В, как и для поля Е, справедлив принцип суперпозиции: поле В, создаваемое в данной точке множеством элементов ∆l с током i (т.е. проводом L с током i), равно векторной сумме полей ∆В от каждого элемента: В= В_k, или, в пределе,

В=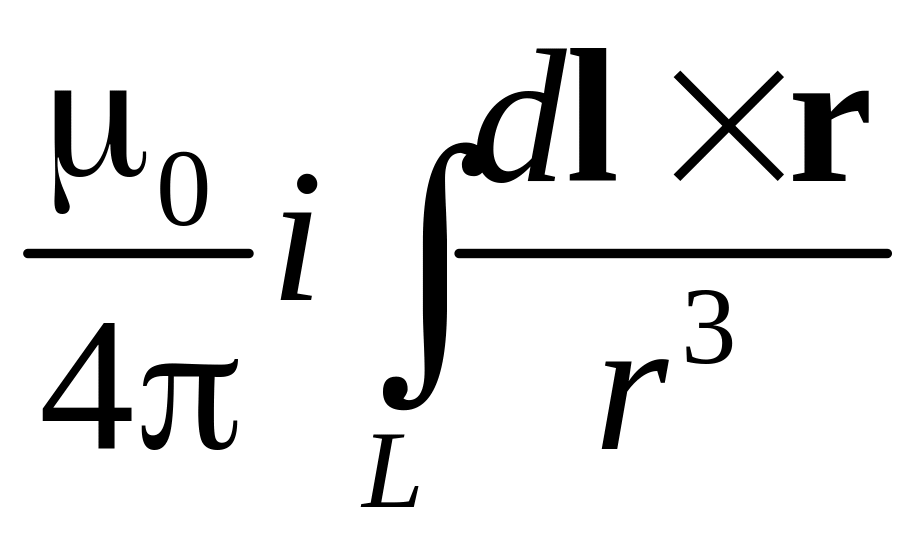 . (6)

Несложно показать, что если формулу (6) применить к тонкому прямому бесконечно длинному проводу с током i, то получим, что создаваемое им магнитное поле (по абсолютной величине)

B= , (7)

где r – расстояние от провода до точки наблюдения. Линии поля В – это концентрические окружности, ориентированные правым винтом относительно стрелки тока, а точнее – относительно вектора плотности тока j.

1.4. Взаимодействие параллельных проводов с токами.

Определение ампера

Формулы (2) и (4) совместно определяют характер взаимодействия двух проводников с токами. В частности, если такими проводниками являются два прямых тонких длинных и параллельных провода с токами, то погонная сила их взаимодействия F₀ [Н/м], т.е. сила, приходящаяся на каждый метр их длины, легко вычисляется аналитически с помощью формул (2) и (7). Покажем это.

П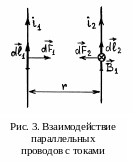 усть в двух таких проводах, находящихся на расстоянии r друг от друга, текут токи i₁ и i₂ «одного направления», т.е. j₁↑↑j₂. Согласно (7), первый провод создает на линии второго поле В₁=μ₀i₁/(2πr), направленное перпендикулярно плоскости двух проводов, как показано на рис. 3. В этом поле на каждый элемент dl₂ второго провода действует сила Ампера dF₂= =i₂(dl₂×B₁), направленная к первому проводу, так что по модулю . Следовательно, на единицу длины второго провода будет действовать сила

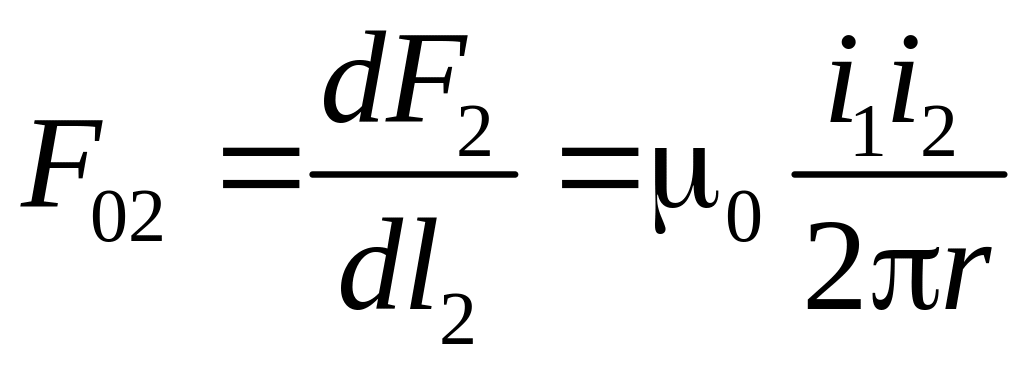[Н/м] (8)

Из-за симметрии системы такая же по величине сила притяжения F₀₁, будет действовать и со стороны второго провода на единицу длины первого, т.е. F₀₁=−F₀₂. Таким образом, два параллельных провода с однонаправленными токами притягиваются друг к другу с погонной силой (8).

Если теперь положить i₁=i₂=1 ед. тока СИ, а r=1 м, то погонная сила взаимодействия параллельных проводов

F₀= 2·10⁻⁷ [Н/м].

Соответствующая единица тока в системе СИ названа ампером и принята за одну из основных единиц СИ (в отличие, например, от кулона, который является производной единицей и определяется как заряд, переносимый током i =1 А за время t=1 c).

Таким образом, определение ампера следующее: ампер – это ток, который, протекая по каждому из двух тонких прямых бесконечно длинных проводов, находящихся в вакууме на расстоянии 1 м, создает между ними погонную силу взаимодействия F₀=2·10⁻⁷ Н/м.