2. Метод

2.1. Определение ёмкости конденсатора

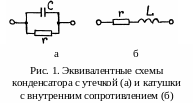
Реальный конденсатор всегда имеет хотя бы ничтожную «утечку». Это следует из того, что если его зарядить и оставить отключённым от генератора на несколько часов или суток, то он в конце концов саморазрядится через своё диэлектрическое заполнение Даже вакуумный конденсатор рано или поздно разрядится за счёт «налипания» на его электроды заряженных частиц из окружающей среды. Поэтому эквивалентную схему реального конденсатора можно представить как параллельно соединённые идеальную ёмкость С и некоторое сопротивление утечки r (рис. 1,а). Однако обычно это сопротивление утечки настолько велико, что стандартный промышленный конденсатор практически можно считать идеальной ёмкостью без утечки. Тогда на частоте ω полное сопротивление конденсатора без учёта утечки будет состоять только из его емкостного сопротивления:

.

Отсюда следует, что для определения ёмкости конденсатора достаточно приложить к нему синусоидальное напряжение U_С и измерить ток I (I и U – эффективные значения): так как , то C=I/(ωU_C). А чтобы обойтись и без амперметра, последовательно с конденсатором удобно включить резистор с заранее известным сопротивлением R (образцовый резистор) и измерить напряжение U_R на нём. Тогда I=U_R/R и

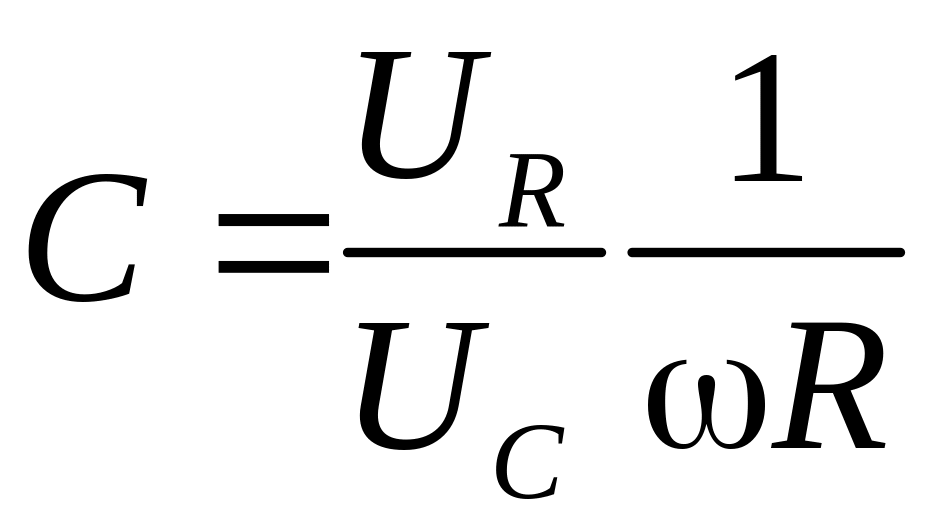. (1)

Эта формула и является рабочей для определения ёмкости конденсатора.

2.2. Определение индуктивности катушки

Эквивалентная схема реальной катушки показана на рис. рис. 1,б, где L – идеальная индуктивность, r – внутреннее активное сопротивление проводов обмотки. В отличие от конденсатора, здесь активным сопротивлением r пренебрегать, как правило, уже нельзя, так как на низких частотах оно может быть соизмеримо с индуктивным сопротивлением ωL и даже больше его. Таким образом, в отличие от конденсатора, катушка имеет два неизвестных параметра – L и r, входящие в её полное сопротивление

.

L и r можно определить, если составить два независимые уравнения Ома, содержащие эти параметры. Но в катушке элементы L и r физически неразделимы, так что измерения тока и напряжения на ней дадут лишь одно уравнение:

,

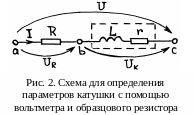
где I – ток через катушку (эффективное значение, измеряемое амперметром), U_к – напряжение на ней (эффективное значение, измеряемое вольтметром). Чтобы получить пару уравнений, проще всего подключить к катушке последовательно резистор с известным сопротивлением R (рис. 2). Тогда, применяя закон Ома к участкам ab, bc и ас, получаем три уравнения относительно трёх неизвестных – I, L и r: IR=U_R, IZ_к=U_к, IZ_ac=U. Подставив ток I из первого уравнения во второе и третье, получаем систему двух уравнений относительно неизвестных L и r:

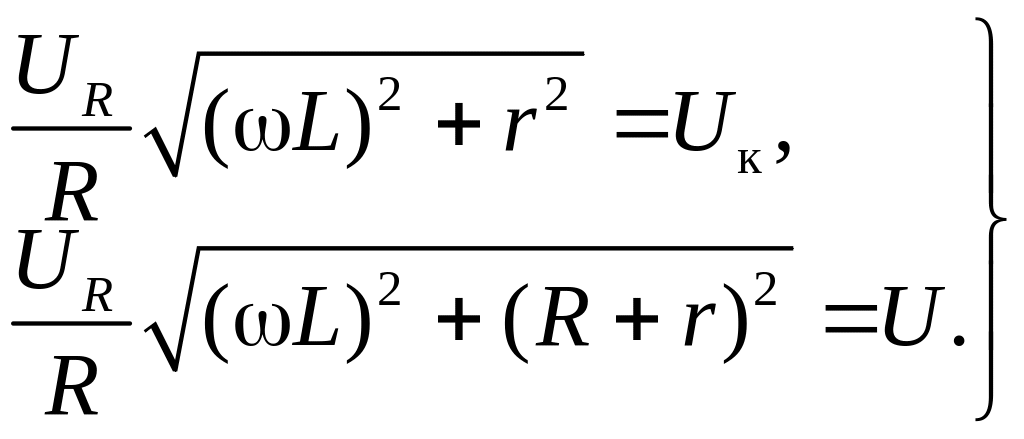
Из этой системы удобно сначала определить активное сопротивление катушки:

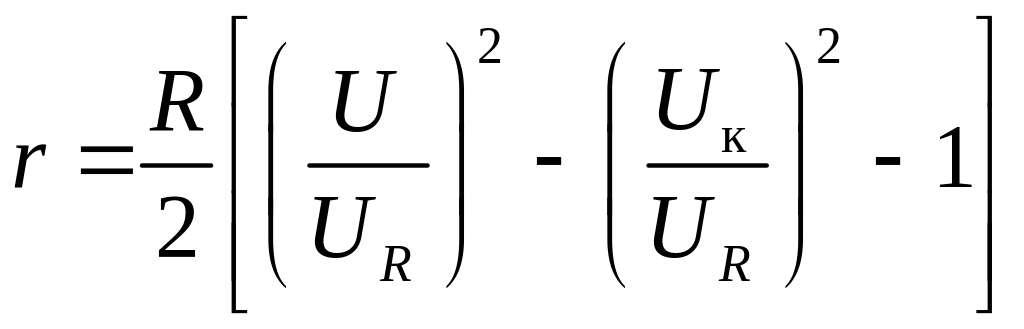, (2)

а уже через него затем выразить и реактивное:

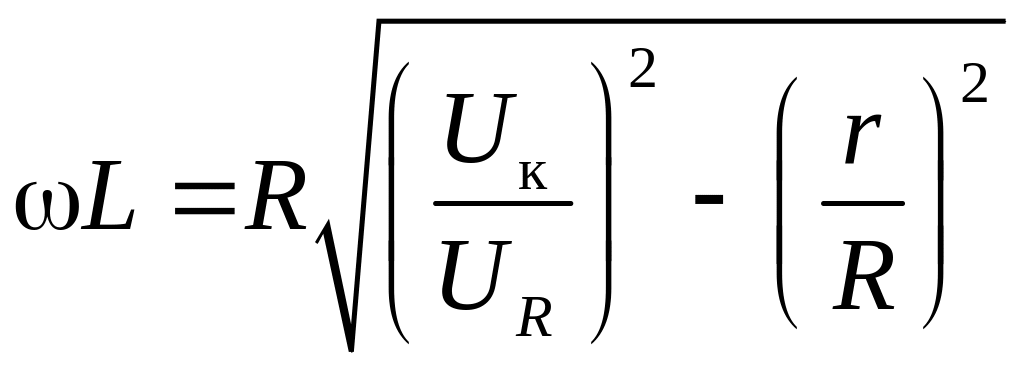. (3)

Следует отметить, что для достаточно точного определение r и L по формулам (2) и (3) необходимо, чтобы величины R, ωL и r на рабочей частоте были соизмеримы, иначе малая погрешность при измерении напряжений U, U_R и U_к приведёт к большой ошибке по r и L.

И ещё одно замечание. Параметр r проще было бы измерить на постоянном токе: r=U_к/I₌ (индуктивное сопротивление при этом пропадает). Однако определённая таким образом величина, называемая омическим сопротивлением катушки, будет отличаться от её активного сопротивления, которое вследствие скин-эффекта зависит от частоты и всегда больше омического. При частотах в несколько десятков герц ото отличие невелико: например, для прямого провода оно практически незаметно, хотя для того же провода, но свитого в катушку, отличие может быть раза в два. При частотах же в тысячи герц, а там более в мегагерцы, активное сопротивление может уже во много раз превысить омическое.