1.3. Простой мост

Д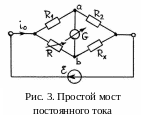 ля лучшего уяснения работы двойного моста рассмотрим сначала (или вспомним), как работает простой мост постоянного тока. Его схема показана на рис. 3.

Простой мост (мост Уитстона) состоит из четырёх сопротивлений: известных R₁, R₂, R и неизвестного R_х, которые называются плечами моста и образуют четырёхугольник. В одну из диагоналей моста (аb) включается чувствительный гальванометр G, а в другую − генератор постоянного напряжения , создающий ток i₀. Сопротивления R₁и R₂ фиксированы, а величину R можно варьировать. Несложно показать, что мост сбалансирован, т.е. ток в диагонали ab равен нулю, если равны произведения перекрёстных сопротивлений: R₁R_x=RR₂. Это означает, что если мы добъёмся баланса моста, варьируя переменное сопротивление R, то неизвестное сопротивление

.

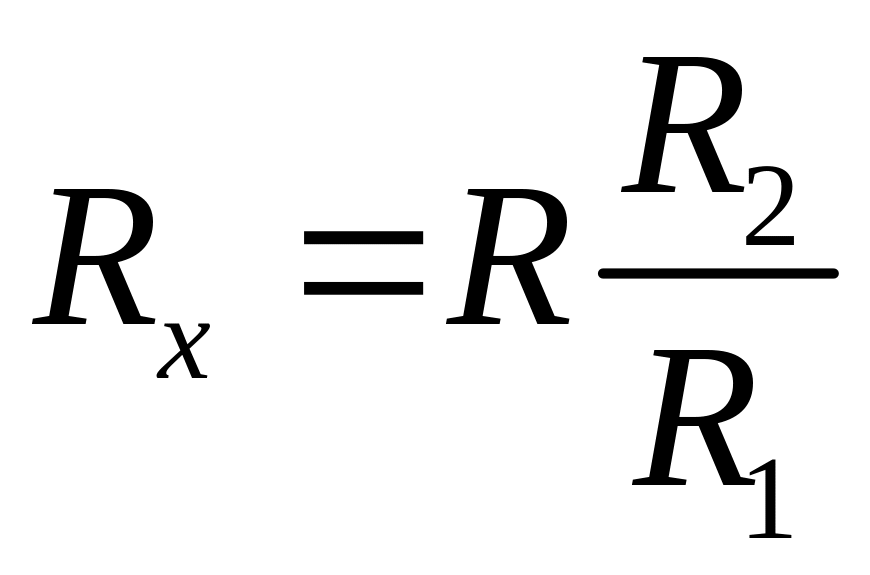А если установить R₂=R₁, то при балансе моста будет совсем просто: R_х=R.

Если сопротивление R полагать эталонным, то точность измерения R_х (относительная погрешность)

δR_x~i_m/i₀,

где i_m – минимальный ток, который может почувствовать гальванометр,

т.е. чувствительность гальванометра. Обычно i_m~10⁻⁶…10⁻⁸ А, но у хороших зеркальных гальванометров чувствительность может достигать и 10⁻⁹ А. В этом случае при рабочем токе i₀=1 мА погрешность измерения R_х теоретически должна составить не более 0,1…0,001%! Реально она значительно больше и определяется уже не чувствительностью гальванометра, а точностью изготовления остальных трёх резисторов моста, которая обычно не лучше 1%. Для прецизионных резисторов δ~0,1%; но для поддержания такой точности уже надо стабилизировать температурный режим. Однако в большинстве практических случаев точность измерения сопротивлений в 1% оказывается вполне достаточной.

Таким образом, главным достоинством мостового метода является то, что он позволяет измерять сопротивления с точностью эталонов. Но это при условии, что сами измеряемые сопротивления не слишком малы: они должны быть намного больше сопротивления соединительных проводов.

Как отмечалось, основной причиной неэффективности обычного мостового метода при измерении малых сопротивлений является паразитное влияние сопротивления соединительных проводов, когда мы фактически меряем не R_х, а R_х+R_пров, причём R_пров здесь может быть больше самогó R_х. Отстроиться от R_пров, но сохранить достоинства обычного мостового метода как особо точного и позволяет так называемый двойной мост.

1.4. Метод двойного моста

П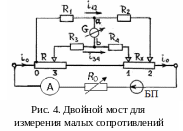 усть требуется измерить малое сопротивление R_х куска провода между точками 1 и 2. Схема двойного моста с включённым в него исследуемым образцом показана на рис. 4. В плечи моста включены:

● в плечо 1 – резистор R₁,

● в плечо 2 – резистор R₂,

● в плечо 3 – резистор R₃, и эталонное малое сопротивление R=R₀₃,

● в плечо 4 – резистор R₄ и измеряемое малое сопротивление R_х=R₁₂.

В одну диагональ моста включён гальванометр G, а в другую – источник тока i₀, состоящий из блока питания БП, регулятора тока R₀ и амперметра А. Сопротивления резисторов R₁, R₂, R₃ и R₄ значительно, на 2-4 порядка больше малых сопротивлений R и R_х, а сами R и R_х соизмеримы.

Схема рис. 4 имеет такой же мостовой вид, как и схема рис. 3, лишь разрисовка моста немного изменена для удобства анализа. Отличие двойного моста от простого состоит только в том, что на рис. 4 сопротивления R и R_х соединены с гальванометром не непосредственно, а через мостик R₃, R₄. Но именно этот мостик и позволяет исключить паразитные сопротивления соединительных проводов. Рассмотрим работу двойного моста.

Так как сопротивления R₁…R₄≫R и R_х, то ответвляемые токи i₁₂ и i₃₄≪i₀. Следовательно, можно считать, что ток, протекающий через R и R_х, практически равен i₀.

Пусть R_пров − характерное сопротивление соединительных проводов на участках 0-а-2 и 3-b-1. Так как R_пров≪R₁…R₄, то падение напряжения на проводах в ветвях 0-а-2 и 3-b-1 пренебрежимо мало по сравнению с напряжениями на самих R₁…R₄. Но оно мало и по сравнению с напряжениями на R и R_х, так как, хотя сопротивления R и R_х и соизмеримы с R_пров, но ток i₀ через них намного больше токов i₁₂ и i₃₄. Напряжения же на R и R_х соизмеримы с напряжениями на R₁, R₂, R₃ и R₄. Следовательно, двойной мост исключает паразитные сопротивления проводов ветвей 0-а-2 и 3-b-1.

Запишем теперь вторые уравнения Кирхгофа для двух контуров моста в режиме баланса, т.е. когда i_ab=0 (потенциалы точек a и b при этом равны и эти точки могут быть соединены):

для левого контура моста: i₁₂R₁=i₀R+i₃₄R₃;

для правого контура моста: i₁₂R₂=i₃₄R₄+i₀R_х.

Или:

Деля второе уравнение на первое, получаем:

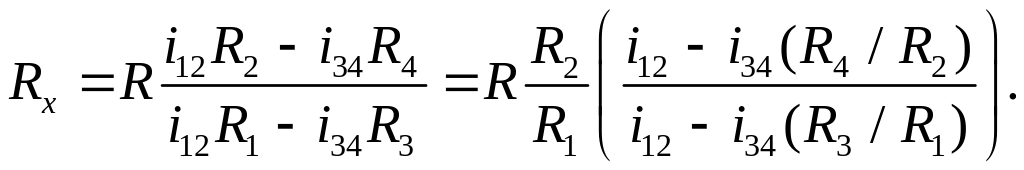
Если подобрать R₁, R₂, R₃ и R₄ так чтобы R₄/R₂=R₃/R₁, т. е. чтобы

, (3)

то баланс моста будет при

. (4)

Видно, что при выполнении условия (3) результат (4) не зависит от тока i₃₄, а значит и от сопротивления участка 3-1, которые связаны вторым уравнением Кирхгофа: i₃₄(R₃+R₄)=i₀R₃₁.

Формула (4) и является рабочей для определения сопротивления R_х исследуемого проводника. При выполнении условия (3) баланс моста достигается варьированием только сопротивления R.

Если ожидаемое сопротивление R_х соизмеримо с R, то можно взять R₁=R₂, R₃=R₄, и тогда R_х=R. Если же ожидаемое R_х≪R, то надо выставлять R₂/R₁, например, 10:1 (тогда таким же надо брать и R₄/R₃).

Практически эталонное сопротивление R представляет собою хорошо откалиброванную проволоку, натянутую вдоль линейки. Контакт 0 фиксирован в самом начале (или вблизи начала) проволоки на делении линейки «0», а контакт 3 – это скользящий ползунок. Такое устройство называется реохордом. Погонное сопротивление проволоки (сопротивление единицы длины) [Ом/м] должно быть точно известно. Тогда R=R₀₃=γl, где l – длина отрезка 0-3. Варьирование R с целью достижения баланса моста осуществляется движением ползунка 3.