1.3.Одношаговые методы типа Рунге–Кутты

1.3.1.Алгоритм

Перейдем к общему случаю системы (18). Одношаговые методы типа Рунге–Кутты имеют вид:

(21)

В дальнейшем для описания конкретных вариантов метода будем пользоваться таблицей Бутчера:

a1	b11	b12	…	b1K
a2	b21	b22	…	b2K
…	…	…	…	…
ak	bK1	bK2	…	bKK
	c1	c2	…	cK

Для явных схем Рунге–Кутты L < k, и таблица Бутчера выглядит следующим образом:

a1	0	0	…	0	0
a2	b21	0	…	0	0
a3	b31	b32	…	0	0
…	…	…	…	…	…
ak	bK1	bK2	…	bKK–1	0
	c1	c2	…	cK–1	cK

В этом случае для расчёта vⁿ⁺¹ по vⁿ в соответствии с (21) имеем простые рекуррентные соотношения:

— предиктор,

(22)

— первый корректор и т. д.

«Полуявные» или «диагонально неявные» схемы Рунге–Кутты отличаются от явных наличием ненулевых элементов на главной диагонали таблицы Бутчера (L≤k):

a1	b11	0	…	0
a2	b21	b22	…	0
…	…	…	…	…
ak	bK1	bK2	…	bKK
	c1	c2	…	cK

В этом случае на каждом шаге по времени последовательно решаются нелинейные системы:

,

и т. д.; например, методом Ньютона:

   

с неким начальным значением , например, .

В общем случае ( L = K ), обозначая r = {r₁, …, r_k}, имеем еще более громоздкую нелинейную систему

R(r) = 0, где R = {R₁, R₂, …, R_K}

и итерационный процесс для ее решения

.

1.3.2.Аппроксимация

Параметры схемы (неопределенные пока коэффициенты a₁, …, a_K; c₁, …, c_K; b₁₁, …, b_1K, …, b_K1, …, b_KK), конечно, не произвольны. Их (все или часть) находят, прежде всего, из условий аппроксимации, получаемых из разложения (21) в ряд в точке t = tⁿ или t = tⁿ⁺¹ с учетом (18) и его следствий

v_t = f(t, v),

(т. е. рассматривая аппроксимацию на решениях (18)).

Поскольку в (21) при r_k стоит множитель τ, то в разложении правой части (21) нужно удерживать на один член ряда меньше, чем в левой. Индекс n будем опускать. Итак, левая часть (21):

Далее:

Если коэффициенты a_k выбирать таким образом, чтобы

, (23)

то Подставляя эти разложения в (21) и группируя члены при одинаковых степенях τ, получим (после деления на τ )

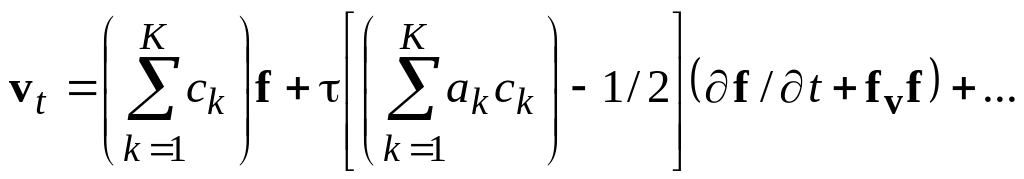
Очевидно, что при выполнении условия (вместе с (23))

(24)

обеспечивается 1-й порядок аппроксимации, при

(25)

(вместе с (23), (24)) — 2-й порядок аппроксимации. Условия 3-го порядка точности (вместе с (23) – (25)) есть

, (26)

а условия 4-го порядка (вместе с (23) – (26)):

,

(27)

.

Уравнения (23) – (27) составляют относительно неопределенных коэффициентов некоторую нелинейную систему. Очевидно, что привлекаемое число условий аппроксимации (т. е. порядок точности схемы р при выполнении соответствующих условий гладкости) должно быть меньше числа отличных от нуля коэффициентов в (21), и соответствующая система должна быть разрешима. В частности, для явных схем , а для общих неявных схем .