5 Аддитивные и мультипликативные погрешности

В зависимости от характера изменения величины погрешности при изменении измеряемой величины погрешности делятся на аддитивные и мультипликативные.

Аддитивные погрешности обусловлены смещением статической характеристики прибора вверх или вниз (вправо или влево), например, за счет смещения шкалы.

y = k(x+∆x)

y yи^{= kx}

∆y

y = k(x-∆x)

x

Рис. 2 Влияние аддитивных погрешностей на статическую характеристику прибора:

y_и - идеальная статическая

характеристика, y - фактическая статическая характеристика

Влияние аддитивных погрешностей на статическую характеристи-

ку прибора показано на рис. 2.

Аддитивная погрешность (при выражении ее в виде абсолют- ной погрешности) имеет постоянную величину, не зависящую от значения измеряемой величины х:

∆y = y - y_и = k(x+∆x) - kx = k∆x = = const, так как k = const,

∆x = const.

При выражении аддитивной погрешности в виде относительной по- грешности получаем

δy = ∆y/y_и = k∆x/kx = ∆x/x = var, так как ∆x = const, x = var.

Аддитивные погрешности преобладают у большинства стрелочных приборов.

Мультипликативные погрешности возникают из-за погрешностей задания передаточного коэффициента k статической характеристики y = kx.

Влияние мультипликативных погрешностей на статическую характеристику прибора показано на рис.3.

Мультипликативная погрешность (при выражении ее в виде абсолютной погрешности) пропорцио-

y = (k+∆k)x

∆y y yи ^{= kx}

^{y = (k-∆k)x}

нальна значению измеряемой величины:

∆y = y - y_и = (k + ∆k)x -

- kx = ∆kx = var, так как

∆k = const, x = var.

При выражении мультипликативной погрешности в виде отно- сительной погрешности по-

x

Рис. 3

относительная погрешность.

лучим:

δy = ∆y/y_и = ∆kx/kx = ∆k/k =const, так как ∆k =

const,

т.е. у приборов с преобладающими

мультипликативными

погрешностями

постоянной остается

y yи = kx

x

Рис. 4

Мультипликативные погрешности преобладают у

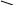
приборов, относящихся к масштабирующим преобразователям (шунты, добавочные сопротивления, усилители, делители, трансформаторы и т.п.).

Существуют приборы, у которых аддитивные и мультипликативные погрешности соизмеримы. К этому классу приборов относятся цифровые приборы. Влияние соизмеримых аддитивных и мультипликативных погрешностей на статическую характеристику прибора показано на рис. 4.

6 Классы точности средств измерений

Класс точности - это обобщенная характеристика средства измерений, выражаемая пределами допускаемых значений его основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность. Класс точности не является непосредственной оценкой точности измерений, выполняемых этим средством измерений, поскольку погрешность зависит еще от ряда факторов: метода измерений, условий измерений и т.д. Класс точности лишь позволяет судить о том, в каких пределах находится погрешность средства измерений данного типа.

Государственными стандартами для разных приборов установлены различные классы точности, которые обычно указывают на шкале или корпусе прибора. Средство измерений может иметь два и более класса точности. Например, при наличии у него двух или более диапазонов измерений одной и той же физической величины ему можно присваивать два или более класса точности. Приборы, предназначенные для измерений нескольких физических величин, также могут иметь различные классы точности для каждой измеряемой величины.