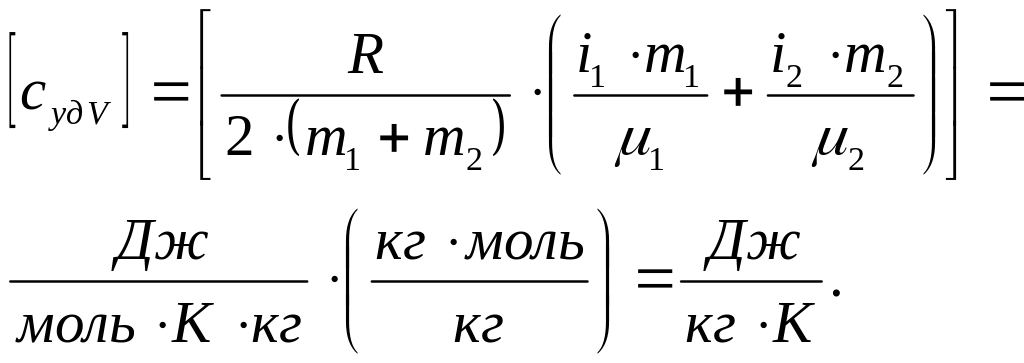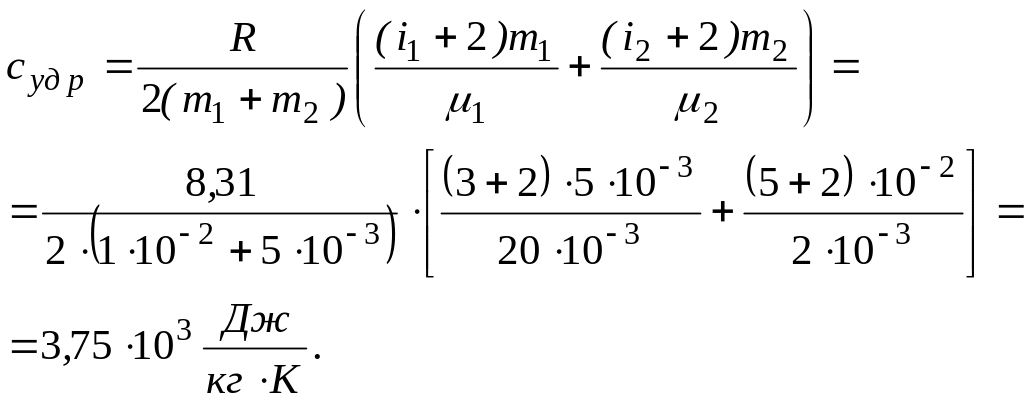2.2. Примеры решения задач

Пример 1. Шар массой т₁ = 0,5 кг, движущийся горизонтально с некоторой скоростью, столкнулся с неподвижным шаром массой т₂ = 200 г (рис. 2.1). Шары абсолютно упругие, удар прямой, центральный. Какую долю в своей кинетической энергии первый шар передал второму?

Дано:

т₁ = 0,5 кг

т₂ = 200 г = 0,2 кг

 = ?

Рис. 2.1

Решение. Доля энергии, переданной первым шаром второму, выразится соотношением

, (2.1)

где – кинетическая энергия первого шара до удара; U₂ и скорость и кинетическая энергия второго шара после удара.

Как видно из формулы (2.1), для определения  надо найти U₂. Согласно условию задачи, сумма импульсов системы двух шаров относительно горизонтального направления не изменяется, и механическая энергия шаров в другие ее виды не переходит. Пользуясь этим, найдем

; (2.2)

. (2.3)

Решая совместно уравнения (2.2) и (2.3), найдем U₂:

.

Подставив выражение U₂ в формулу (2.1) и сократив на V₁ и m₁, получим

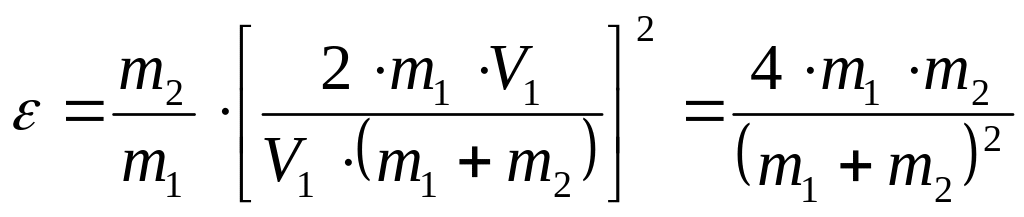. (2.4)

Из найденного соотношения видно, что доля переданной энергии зависит только от масс сталкивающихся шаров.

Проверим размерность:

.

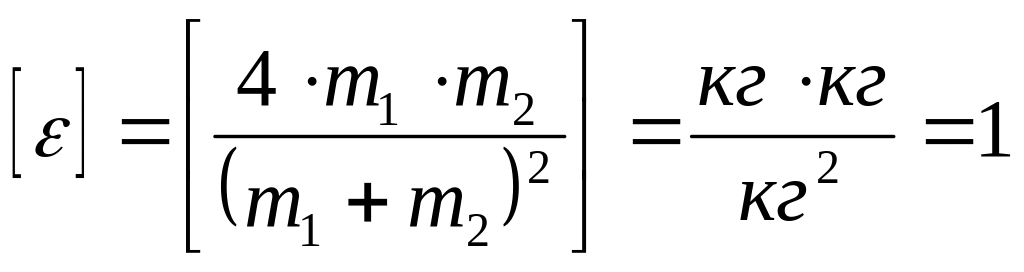Подставим в (2.4) числовые значения и произведем вычисления:

.

Ответ. Первый шар передал второму шару 0,8 своей первоначальной энергии.

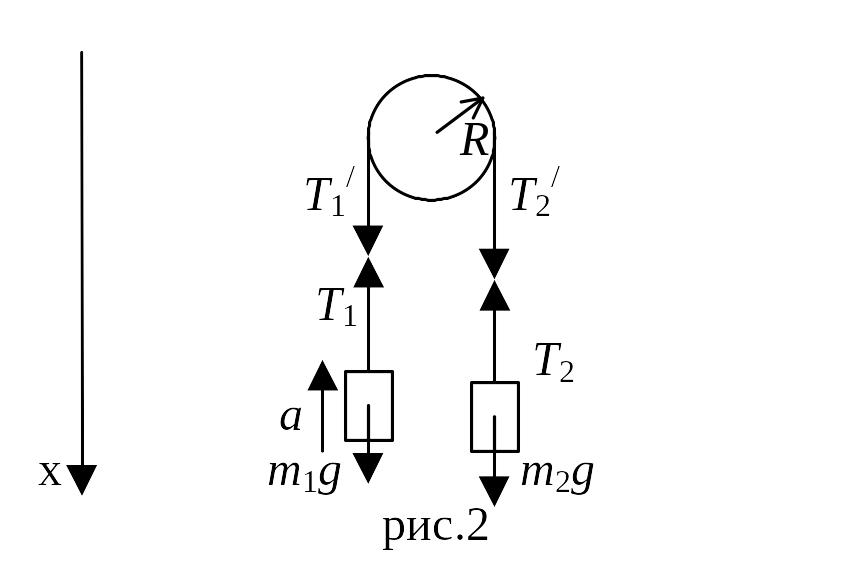
Пример 2. Через блок в виде сплошного диска, имеющего массу m = 80 г (рис. 2.2), перекинута тонкая гибкая нить, к концам которой подвешены грузы с массами m₁ = 100 г и m₂ = 200 г. Определить ускорение, с которым будут двигаться грузы, если их предоставить самим себе. Трением и массой пренебречь.

Рис. 2.2

Дано:

m₁ = 100 г = 0,1 кг

m₂ = 200 г = 0,2 кг

g = 9,8 м/с²

а - ?

Решение. Рассмотрим силы, действующие на каждый груз и на блок в отдельности. На каждый груз действует две силы: сила тяжести и сила упругости (сила натяжения нити). Направим ось x вертикально вниз и напишем для каждого груза уравнение движения (второй закон Ньютона) в проекциях на эту ось. Для первого груза

, (2.5)

для второго груза

. (2.6)

Под действием моментов сил Т₁^/ и T₂^/ относительно оси z, перпендикулярной плоскости чертежа и направленной за чертеж, блок приобретает угловое ускорение . Согласно основному уравнению динамики вращательного движения

, (2.7)

где – момент инерции блока (сплошного диска) относительно оси z;  = a/r.

Согласно третьему закону Ньютона, с учетом невесомости нити Т₁^/=Т₁, T₂^/=Т₂. Воспользовавшись этим, подставим в уравнение (2.7) вместо Т₁^/ и T₂^/ выражения Т₁ и Т₂, получив их предварительно из уравнений (2.5) и (2.6):

.

После сокращения на r и перегруппировки членов найдем

. (2.8)

Проверим размерность:

.

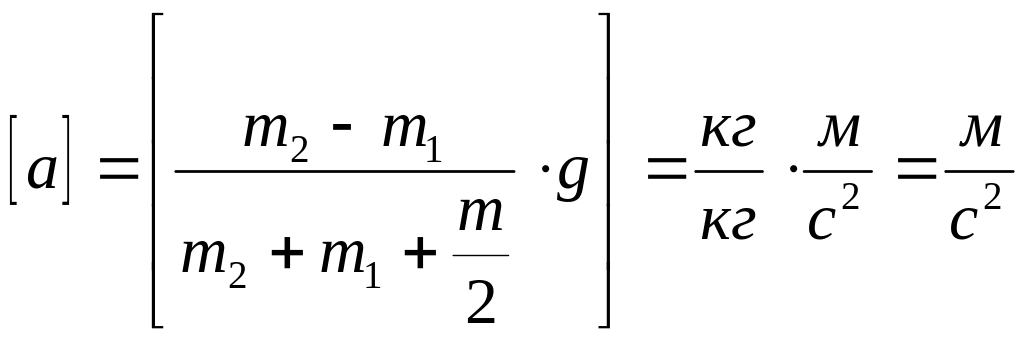После подстановки числовых значений в формулу (2.8) получим

.

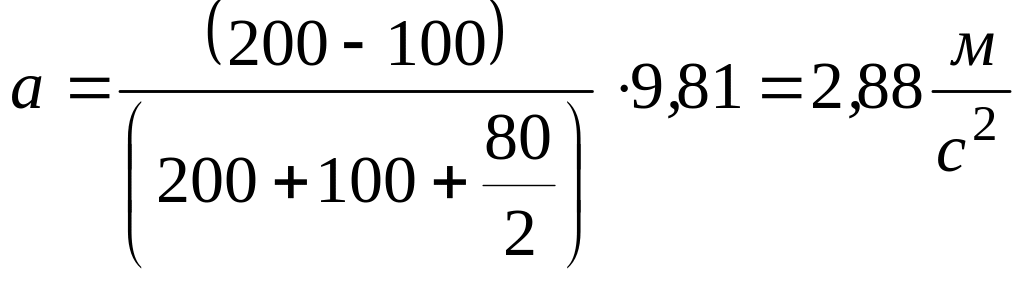Ответ. Грузы будут двигаться с ускорением 2,88 м/с².

Пример 3. Маховик в виде сплошного диска радиусом R = 0,2 м и массой m = 50 кг раскручен до частоты вращения n₁ = 480 мин^-1 и предоставлен сам себе (рис. 2.3). Под действием сил трения маховик остановился через t = 50 с. Найти момент сил трения.

Рис. 2.3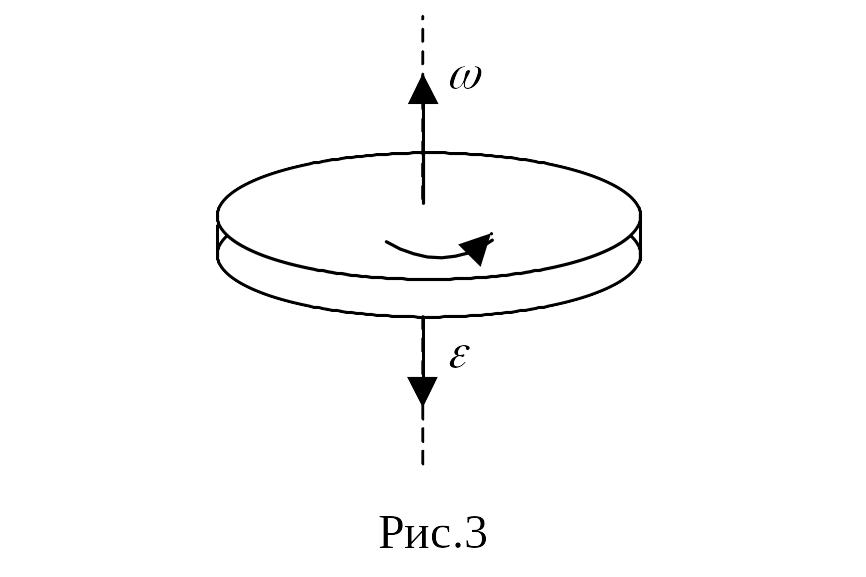

Дано:

R = 0,2 м

m = 50 кг

n₁ = 480 мин^-1 = 8 с^-1

t = 50 с

М - ?

Решение. Воспользуемся основным уравнением динамики вращательного движения в виде

, (2.9)

где dL_z – изменение проекции на ось z момента импульса маховика, вращающегося относительно оси z, совпадающей с геометрической осью маховика, за интервал времени dt; M_z – результирующий момент внешних сил (в данном случае момент сил трения), действующей на маховик относительно оси z.

Момент сил трения можно считать не изменяющимся с течением времени (M_z=const), поэтому интегрирование уравнения (2.9) приводит к выражению

. (2.10)

При вращении твердого тела относительно неподвижной оси изменение проекции момента импульса равно

, (2.11)

где I_z момент инерции маховика относительно оси z;  изменение угловой скорости маховика.

Приравнивая правые части равенств (2.10) и (2.11), получим

,

откуда

. (2.12)

Момент инерции маховика в виде сплошного диска определяется по формуле

.

Изменение угловой скорости =₂-₁ выразим через конечную n₂ и начальную n₁ частоты вращения, пользуясь соотношением =2n:

.

Подставив в формулу (2.12) выражения для  и I_z, получим

. (2.13)

Проверим, дает ли расчетная формула единицу измерения момента силы (Нм). Для этого в правую часть формулы вместо символов величин подставим их единицы:

.

Подставим в формулу (2.13) числовые значения величин и произведем вычисления:

.

Знак «минус» показывает, что момент сил трения оказывает на маховик тормозящее действие.

Ответ. Момент сил трения равен М = –1 Нм.

Пример 4. Платформа в виде сплошного диска радиусом R = 1,5 м и массой m₁ = 180 кг вращается вокруг вертикальной оси с частотой n=10 мин^-1. В центре платформы стоит человек массой m₂ = 60 кг. Какую линейную скорость V относительно пола помещения будет иметь человек, если он перейдет на край платформы?

Дано:

R = 1,5 м

m₁ = 180 кг

n = 10 мин = 1/6 с^-1

m ₂ = 60 кг

V – ?

Решение. Согласно условию задачи, момент внешних сил относительно оси вращения z, совпадающей с геометрической осью платформы, можно считать равным нулю. При этом условии проекция момента импульса системы «платформа – человек» остается постоянной:

, (2.14)

где I_z – момент инерции платформы с человеком относительно оси z;  – угловая скорость платформы.

Момент инерции системы равен сумме моментов инерции тел, входящих в состав системы, поэтому в начальном состоянии I_z=I₁+I₂, а в конечном состоянии I_z^/=I₁^/+I₂^/. С учетом этого равенство (2.14) примет вид

, (2.15)

где значения моментов инерции I₁ и I₂ платформы и человека соответственно относятся к начальному состоянию системы; I₁^/ и I₂^/ - к конечному.

Момент инерции платформы относительно оси при переходе человека не изменяется: I₁=I₁^/=m₁R²/2. Момент инерции человека относительно той же оси будет изменяться. Если рассматривать человека как материальную точку, то его момент инерции I₂ в начальном состоянии (в центре платформы) можно считать равным нулю. В конечном состоянии (на краю платформы) момент инерции человека I₂=m₂R².

Подставим в формулу (2.15) выражения моментов инерции, начальной угловой скорости вращения платформы с человеком (=2n) и конечной угловой скорости (^/=V/R, где V – скорость человека относительно пола):

.

После сокращения на R² и простых преобразований находим скорость V:

.

Проверим единицы измерения:

.

Произведем вычисления:

.

Ответ. При переходе человека на край платформы его скорость относительно пола помещения равна 1 м/с.

Пример 5. Ракета установлена на поверхности Земли для запуска в вертикальном положении. При какой минимальной скорости V₁, сообщенной ракете при запуске, она удалится от поверхности на расстояние, равное радиусу Земли (R = 6,3710⁶ м)? Всеми силами, кроме силы гравитационного взаимодействия ракеты и земли, пренебречь.

Дано:

R = 6,3710⁶ м

g = 9,81 м/с²

V₁ – ?

Решение. Со стороны Земли на ракету действует сила тяжести, являющейся потенциальной силой. При неработающем двигателе под действием потенциальной силы механическая энергия ракеты меняться не будет. Следовательно,

, (2.16)

где Е_к1, Е_п1 и Е_к2, Е_п2 – кинетическая и потенциальная энергии ракеты после выключения двигателя в начальном (у поверхности Земли) и в конечном (на расстоянии, равном радиусу Земли) состояниях.

Согласно определению кинетической энергии,

.

Потенциальная энергия ракеты в начальном состоянии:

.

По мере удаления ракеты от поверхности Земли потенциальная энергия возрастает, а кинетическая – убывает. В конечном состоянии кинетическая энергия Е_к2 станет равной нулю, а потенциальная – достигнет максимального значения:

.

Подставляя выражения Е_к1, Е_п1, Е_к2, и Е_п2 в уравнение (2.16), получаем

,

откуда

.

Заметив, что (g – ускорение свободного падения у поверхности Земли), перепишем эту формулу в виде

,

что совпадает с выражением для первой космической скорости.

Сделаем проверку размерности:

.

Произведем вычисления:

.

Ответ. При скорости 7,9 км/с ракета удаляется от Земли на расстояние, равное радиусу Земли.

Пример 6. Сплошной однородный диск колеблется вокруг оси, перпендикулярной плоскости диска и проходящей через край диска (рис. 2.4). Найти радиус диска, если приведенная длина этого физического маятника равна 0,15 м.

Рис. 2.4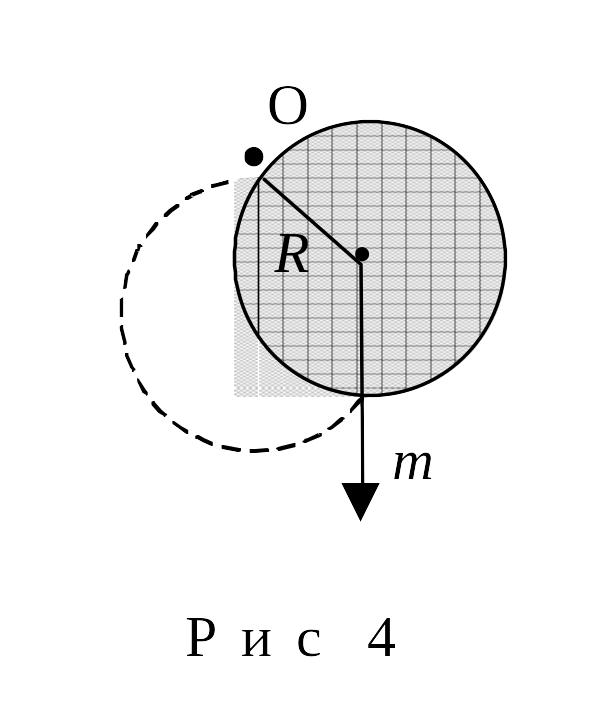

Дано:

L=0,15 м

R - ?

Решение. Период колебаний гармонического маятника может быть рассчитан двояко:

или

,

где I – момент инерции диска относительно оси вращения, проходящей через точку О; d – расстояние от оси вращения до центра тяжести, в данном случае d=R.

. (2.17)

Из уравнения (2.17) находим

. (2.18)

По теореме Штейнера

,

где I₀ – момент инерции относительно оси, параллельной оси вращения и проходящей через центр тяжести. Для диска

.

Итак,

.

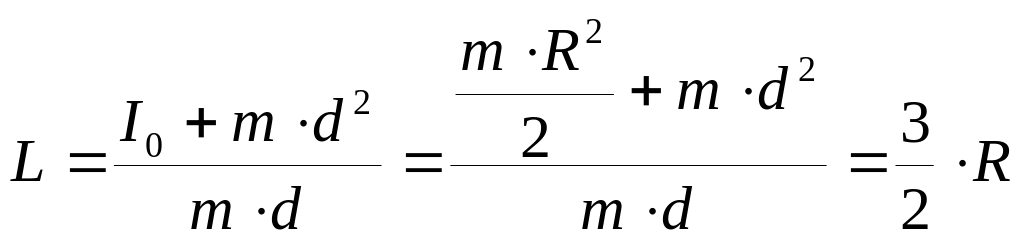Отсюда находим

.

Делаем расчет:

.

Ответ. Радиус диска должен быть 0,10 м.

Пример 7. Верхний конец стержня закреплен неподвижно, к нижнему концу подвешен груз массой m = 2000 кг (рис. 2.5). Длина стержня l₀ = 5 м, сечение S = 4 см². Определить нормальное напряжение  материала стержня, абсолютное l и относительное  его удлинения и потенциальную энергию Е_п растянутого стержня.

Д

Рис. 2.5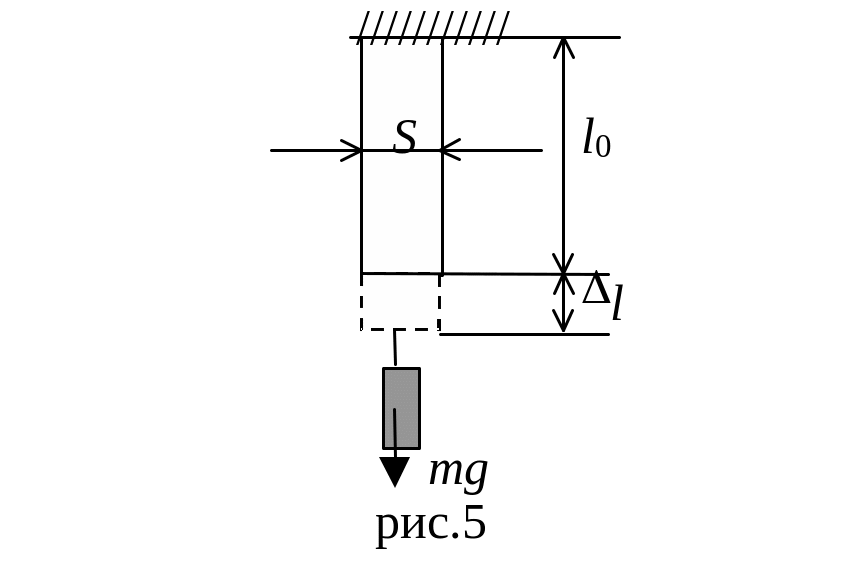

ано:

т = 2000 кг = 210³ кг

l₀ = 5 м

S = 4 см² = 410^-4 м²

Е = 210¹¹ Н/м²

 - ? l -?  -? Е_п -?

Решение. Нормальное напряжение материала растянутого стержня найдем по формуле

, (2.19)

где F – сила, действующая вдоль оси стержня.

В нашем случае сила F равна весу груза P=mg, поэтому формула (2.19) примет вид

. (2.20)

Для нахождения относительного удлинения воспользуемся за-коном Гука:

, (2.21)

где Е – модуль Юнга.

Тогда из формулы (2.21) получим

. (2.22)

Используя определения относительного удлинения, найдем абсолютное удлинение:

. (2.23)

Потенциальная энергия упруго деформированного стержня:

. (2.24)

Произведем проверку единиц измерения:

;

;

;

.

Делаем расчет, используя уравнения (2.20), (2.22)–(2.24):

;

;

;

.

Ответ. Нормальное напряжение стержня  = 4,910⁷ Н/м² при абсолютной деформации l = 1,2310⁸ м. Относительное удлинение  = 2,4510^-4, и потенциальная энергия Е_п = 12,1 Дж.

Пример 8. Найти среднюю кинетическую энергию _вр вращательного движения одной молекулы кислорода при температуре Т = 350 К, а также кинетическую энергию Е_к вращательного движения всех молекул кислорода массой m = 4 г.

Дано:

Т=350 К

m=4 г=410^-2 кг

=3210^-3 кг/моль

k=1.3810^-23 Дж/К

N_A=6.0210²³ 1/моль

_вр -? Е_к - ?

Решение. На каждую степень свободы молекулы газа приходится одинаковая средняя энергия

,

где k – постоянная Больцмана, Т – термодинамическая температура газа.

Так как вращательному движению двухатомной молекулы (молекула кислорода – двухатомная) соответствует две степени свободы, то средняя энергия вращательного движения молекулы кислорода

.

Кинетическая энергия вращательного движения всех молекул газа

. (2.25)

Число всех молекул газа

, (2.26)

где N_A – постоянная Авогадро,  – количество вещества.

Если учесть, что количество вещества , где m – масса газа,  – молярная масса газа, то формула (2.26) примет вид

.

Подставив это выражение в формулу (2.25), получаем

.

Проверим единицы измерения:

;

.

Произведем вычисления:

;

Ответ. Кинетическая энергия вращательного движения одной молекулы Дж; всех молекул

Пример 9. В баллоне объемом V = 10 л находится гелий под давлением р₁ = 1 МПа при температуре Т₁ = 300 К. После того как из баллона было взято т = 10 г гелия, температура понизилась до Т₂ = 290 К. Определить давление р₂ гелия, оставшегося в баллоне.

Дано:

V = 10 л = 10^-2 м³

р₁ = 1 МПа = 10⁶Па

Т₁ = 300 К

т = 10 г = 10^-2 кг

R = 8,32 Дж/мольК

 = 410^-3 кг/моль

р₂ = ?

Решение. Для решения задачи воспользуемся уравнением Менделеева-Клапейрона, применив его к конечному состоянию газа:

, (2.27)

где т₂ – масса гелия в баллоне в конечном состоянии,  – молярная масса гелия, R – универсальная газовая постоянная.

Из уравнения (2.27) выразим искомое давление:

. (2.28)

Массу т₂ гелия выразим через массу т₁, соответствующую начальному состоянию, и массу т гелия, взятого из баллона:

. (2.29)

Массу т₁ гелия найдем также из уравнения Менделеева – Клапейрона, применив его к первоначальному состоянию:

. (2.30)

Подставив выражение массы т₁ в уравнение (2.29), а затем выражение т₂ в уравнение (2.28), найдем

,

или

. (2.31)

Проверим, дает ли формула (2.31) единицу давления:

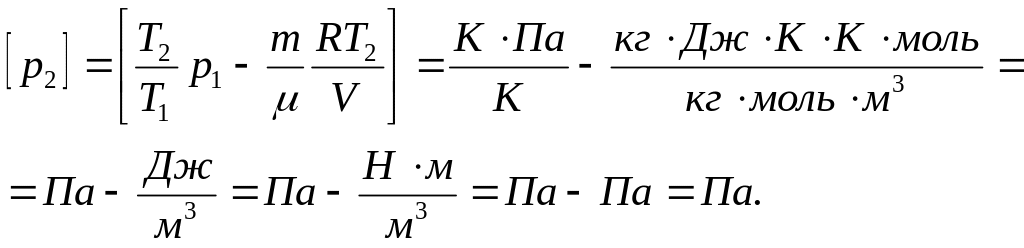
Теперь произведем вычисления:

Ответ. Давление оставшегося газа в баллоне р₂ = 3,6410⁵ Па.

Пример 10. Вычислить удельные теплоемкости с_{уд V} и с_{уд р} смеси неона и водорода, если масса неона т₁ = 5 г, водорода т₂ = 10 г. Газы считать идеальными.

Дано:

т₁ = 5 г = 510^-3 кг

т₂ = 10 г = 110^-3 кг

₁ = 2010^-3 кг/моль

₂ = 210^-3 кг/моль

R = 8,31 Дж/мольК

с_{уд V} = ? с_{уд р} = ?

Решение. Удельную теплоемкость с_{уд V} смеси при постоянном объеме найдем следующим образом. Теплоту, необходимую для нагревания смеси на Т, выразим двумя способами:

;	(2.32)
,	(2.33)

где – удельная теплоемкость неона; – удельная теплоемкость водорода.

Приравняв обе части уравнений (2.32) и (2.33) и разделив обе части полученного равенства на Т, получим

,

откуда

.

(2.34)

Удельные теплоемкости неона и водорода найдем по формуле

,
,

где i₂=5 и i₁=3 – число степеней свободы молекул водорода и неона; R – универсальная газовая постоянная; ₁ и ₂ – молярные массы газов.

Итак,

.	(2.35)

Аналогично найдем , дополнительно учтя, что

и ,
.	(2.36)

Проверим единицы измерения с_{уд V} по формуле (2.35):

Делаем расчет по формулам (2.35) и (2.36):

Ответ. Удельные теплоемкости смеси газов таковы:

и .

Пример 11. Кислород с массой m = 2 кг занимает объем V₁ = 1 м³ и находится под давлением р₁ = 0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема V₂ = 3 м³, а затем при постоянном объеме до давления р₂ = 0,5 МПа (рис. 2.6). Найти изменение U, совершенную им работу А и теплоту Q, переданную газу. Построить график процесса.

Дано:

m = 2 кг

 = 3210^-3 кг/моль

V₁ = 1 м³

р₁ = 0,2 МПа = 210⁵ Па

V₂ = 3 м³

р₃ = 0,5 МПа = 510⁵ Па

U - ? A - ? Q - ?

Рис. 2.6

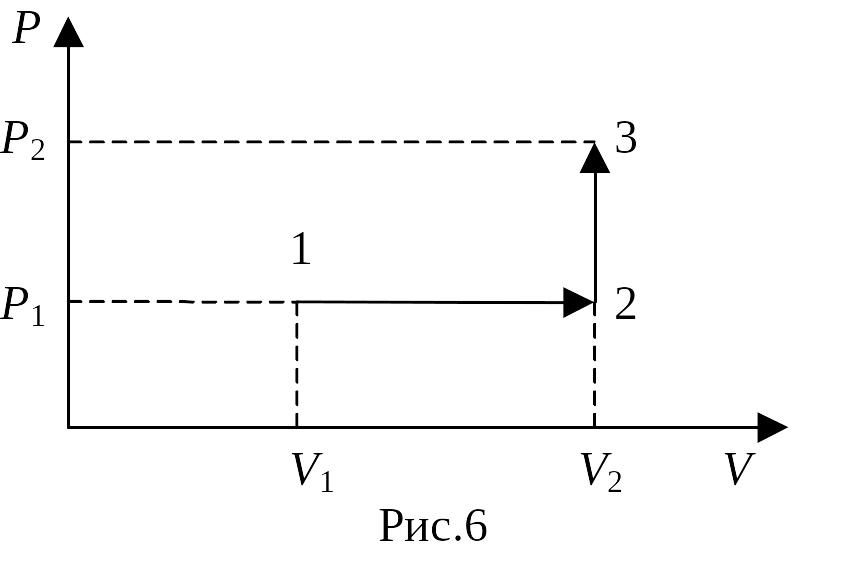
Решение. Найдем изменение внутренней энергии газа:

,

где i – число степеней свободы молекул газа (для двухатомных молекул кислорода i = 5); Т = Т₃ – Т₁ – разность температур газа в конечном (третьем) и начальном состояниях.

Начальную, промежуточную и конечную температуры газа найдем из уравнения Менделеева – Клапейрона:

,

откуда

.

Работа расширения газа при постоянном давлении выражается формулой

.

Работа газа, нагреваемого при постоянном объеме, равна нулю, т.е. А₂ = 0.

Следовательно, полная работа, совершаемая газом,

.

Согласно первому началу термодинамики, теплота Q, переданная газу, равна сумме изменения внутренней энергии U и работы А:

.

5

Проверим единицы измерения:

.

Произведем вычисления:

;
;
;
;
;
;
.

Ответ. В результате переданной теплоты Q = 3,6410⁶ Дж совершена работа А = 0,410⁶Дж; внутренняя энергия изменилась на U = 3,2410⁶ Дж.
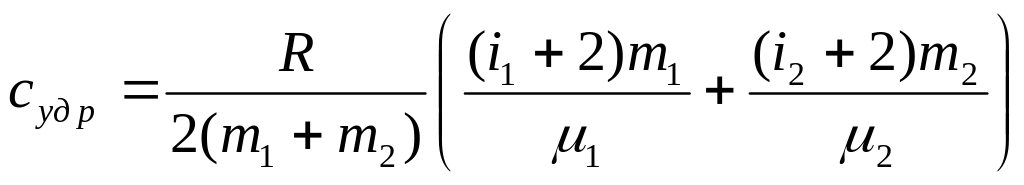