
- •Физика Методические указания и контрольные задания
- •Введение
- •1. Правила оформления контрольных работ и решения задач
- •2. Физические основы механики, молекулярной физики и термодинамики
- •2.1. Перечень формул, которые можно использовать при решении задач без вывода
- •2.2. Примеры решения задач
- •2.3. Задачи
- •3. Физические основы молекулярной физики и термодинамики
- •3.1. Перечень формул, которые можно использовать при решении задач без вывода
- •3.2. Примеры решения задач
- •3.3. Задачи
- •4. Электростатика. Постоянный электрический ток
- •4.1. Перечень формул, которые можно использовать при решении задач без вывода
- •4.2. Примеры решения задач
- •4.3. Задачи
- •5. Электромагнетизм
- •5.1. Перечень формул, которые можно использовать без вывода при решении задач
- •5.2. Примеры решения задач
- •5.3. Задачи
- •6. Волновые процессы
- •6.1. Перечень формул, которые можно использовать без вывода при решении задач
- •6.2. Примеры решения задач
- •6.3. Задачи
- •Справочные данные
- •Основные физические постоянные (округленные значения)
- •Некоторые астрономические величины
- •Плотность твердых тел
- •Массы атомов легких изотопов
- •Периоды полураспада радиоактивных изотопов
- •Масса и энергия покоя некоторых частиц
- •Вопросы для подготовки к экзаменам Механика
- •Механические колебания
- •Молекулярно-кинетическая теория
- •Термодинамика
- •Электростатика
- •Электрическое поле в веществе
- •Постоянный электрический ток
- •Магнитное поле в вакууме
- •Магнитное поле в веществе
- •Электромагнитные явления
- •Волновая оптика
- •Дифракция света
- •Поляризация света
- •Квантовая оптика
- •Элементы квантовой механики
- •Строение и важнейшие свойства ядер
- •Основы квантовой теории твердого тела
- •Рекомендуемая литература
- •Содержание
- •Физика Методические указания и контрольные задания
- •665709, Братск, ул. Макаренко, 40
3. Физические основы молекулярной физики и термодинамики
3.1. Перечень формул, которые можно использовать при решении задач без вывода
Количество вещества – число структурных элементов (молекулы, атомы и т.д.), содержащихся в теле (системе), равно
![]() ,
,
где N – число структурных элементов; NА – число Авогадро (NA = 6,021023 моль-1).
Молярная масса вещества
![]() ,
,
где m – масса тела.
Концентрация молекул
![]() ,
,
где V – объем тела.
Уравнение состояния идеального газа:
![]() ,
,
где Р – давление газа, V – его объем, Т – температура.
Уравнение Менделеева-Клапейрона:
![]() ,
,
где R – универсальная газовая постоянная (R = 8,31 Дж/(мольК)).
Опытные газовые законы для изопроцессов:
а) закон Бойля-Мариотта (изотермический процесс, Т = const):
![]() ;
;
б) закон Гей-Люссака (изобарный процесс, P = const):
![]() ;
;
в) закон Шарля (изохорный процесс, V = const):
![]() ;
;
г) закон Дальтона:
![]() ,
,
где р – давление смеси газов; р1, р2, …, рn – парциальное давление – давление каждой из компонентов смеси.
Основное уравнение молекулярно-кинетической теории газа (уравнение, задающее связь между макро- и микропараметрами):
![]() ,
,
где р – давление газа; п – концентрация молекул газа (число молекул в единице объема); <n> – средняя кинетическая энергия поступательного движения молекул.
Средняя кинетическая энергия молекулы
![]() ,
,
где i – число степеней свободы молекулы; k – постоянная Больцмана (k = 1,3810-23 Дж/К); Т – абсолютная температура.
Зависимость давления газа от концентрации молекул
![]() .
.
Скорости молекул:
а) средняя квадратичная
![]() ,
,
б) средняя арифметическая
![]() ,
,
в) наиболее вероятная
![]() ,
,
где т0 – масса одной молекулы; R – универсальная газовая постоянная; – молярная масса газа.
Средняя длина свободного пробега молекул
![]() ,
,
где d – эффективный диаметр молекул газа.
Среднее число столкновений за единицу времени
![]() .
.
Связь между удельной с и молярной С теплоемкостями
![]() .
.
Молярная теплоемкость газа при постоянном давлении Ср и постоянном объеме Сv
![]() .
.
Уравнение Майера:
![]() .
.
Первое начало термодинамики
![]() ,
,
где Q – количество теплоты, сообщаемое системе; U – изменение внутренней энергии; А – работа, совершаемая газом.
В случае бесконечно малого изменения в системе
![]() .
.
Внутренняя энергия идеального газа
![]() .
.
Работа при изменении объема газа
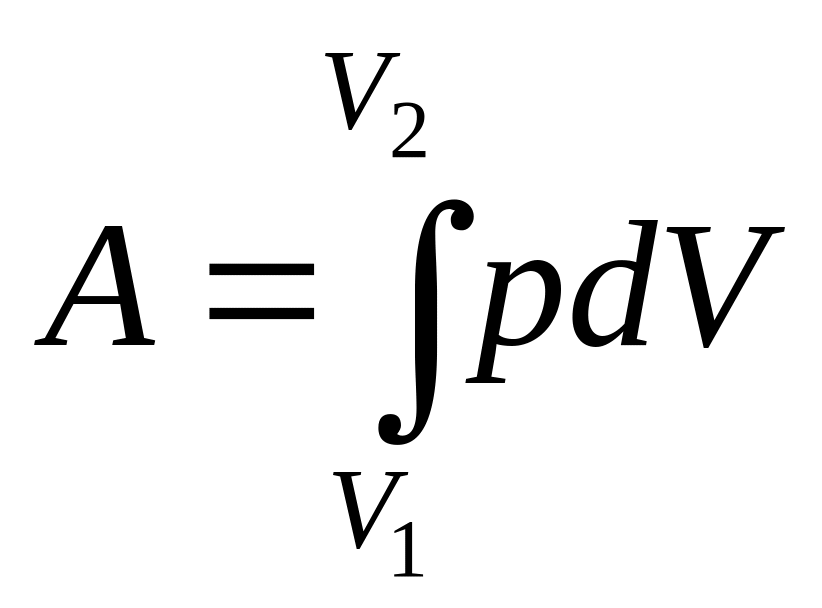 ;
;
при изохорном процессе
![]() ;
;
при изобарном процессе
![]() ;
;
при изотермическом процессе
![]() ;
;
при адиабатном процессе
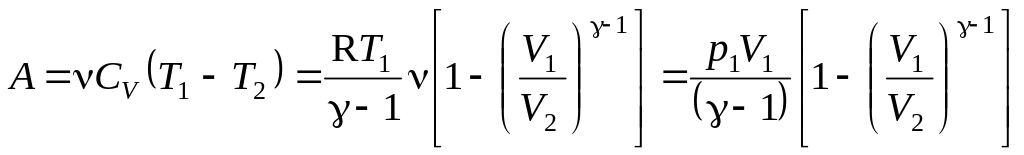 ,
,
где
![]() – показатель адиабаты.
– показатель адиабаты.
Уравнения адиабатного процесса (уравнения Пуассона):
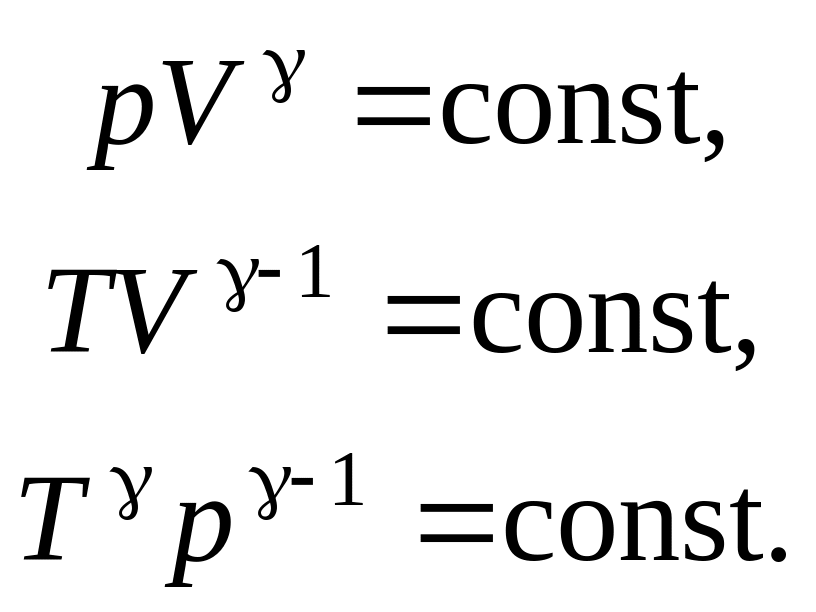
КПД цикла любой тепловой машины
![]() ,
,
где A – работа, совершаемая газом за цикл, Q1 – количество теплоты, получаемое рабочим телом за цикл от нагревателя, Q2 – количество теплоты, отдаваемое за один цикл холодильнику.
Термический коэффициент полезного действия цикла Карно
![]() ,
,
где Т1 и Т2 – соответственно абсолютные температуры нагревателя и холодильника.
3.2. Примеры решения задач
Пример 1. Определить количество вещества и число молекул, содержащихся в 1 г углекислого газа.
Р
Дано: m
= 1 г = 110-3 кг
= 4410-3 кг/моль = ? N
= ?
![]() .
.
Число молекул получим по формуле
![]() .
.
Ответ. Количество вещества = 2,2710-2 моль; число молекул N = 1,41022.
Пример 2. В баллоне объемом 25 л находится водород при температуре Т = 290 К. После того как часть водорода израсходовали, давление баллона понизилось на р = 0,4 МПа. Определить массу израсходованного водорода.
Р
Дано: V
= 25 л = 2510-3 м3 =
210-3 кг/моль Т =
290 К = const
р = 0,4106 Па m
= ?
![]() ,
,
где m1, m2 – масса водорода в начальном и конечном состояниях.
Из уравнения Менделеева-Клапейрона
![]() ,
,
применяя его к начальному и конечному состояниям водорода, найдем m1 и m2:
![]() .
.
Тогда
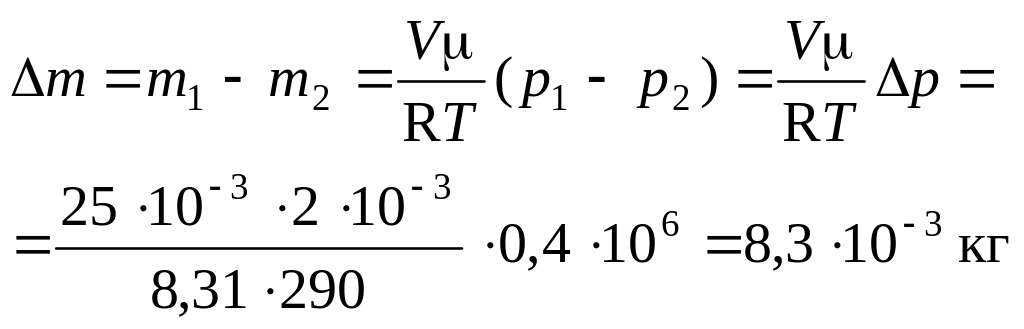
Ответ. Масса израсходованного водорода m = 8,310-3 г.
Пример 3. Количество = 1 кмоль многоатомного газа нагревается на Т = 100 К в условиях свободного расширения. Найти количество теплоты Q, сообщенное газу, приращение U его внутренней энергии и работу А расширения газа.
Р
Дано: =
1 кмоль = 1103
моль i
= 6 Т
= 100 К
р
= const Q
=
?
U
=
?
A
=
?
![]() ,
,
где Ср – молярная теплоемкость газа при постоянном давлении:
![]() ;
;
i – число степеней свободы молекулы.
Исходя из этого,
![]()
![]() .
.
Приращение внутренней энергии вычислим по формуле
![]() ,
,
где
![]() – это молярная теплоемкость газа при
постоянном объеме.
– это молярная теплоемкость газа при
постоянном объеме.
Тогда
![]() ,
,
![]() .
.
Согласно первому началу термодинамики,
![]() .
.
![]() .
.
Ответ. Количество теплоты Q = 3,32 МДж; приращение внутренней энергии U = 2,49 МДж; работа расширения газа A = 0,83 МДж.
Пример 4. Тепловая машина, работающая по циклу Карно, за цикл получает от нагревателя количество теплоты Q1 = 2,5 кДж. Температура нагревателя Т1 = 400 К, температура холодильника Т2 = 300 К. Найти работу А, совершаемую за один цикл, и количество теплоты Q2, отдаваемое холодильнику за один цикл.
Р
Дано: Q1
= 2,5 кДж Т1
= 400 К
Т2 = 300 К А =
? Q2 = ?
![]() ,
,
с другой стороны,
![]() ,
,
откуда
![]()
Вычисляя, получим Q1 = 0,625 кДж.
С другой стороны,
![]() .
.
Тогда
![]() .
.
Вычисляя, получим Q2 = 1,875 кДж.
Ответ. Работа, совершаемая за один цикл А = 0,625 кДж, количество теплоты, отдаваемое холодильнику за один цикл Q2 = 1, 875 кДж.
