2.2.1. Определение расчётных усилий.

Постоянная нагрузка на пролётное строение складывается из собственного веса конструкции и веса мостового полотна. Нормативная нагрузка на 1 пог.м. главной балки определяется , кН/м:

• от собственного веса p₁= 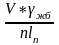= =24,14 кН/м;

• от веса мостового полотна с ездой на балласте р₂= = =17,64 кН/м,

где V и l_п- объём железобетона и полная длина пролётного строения;

n- число главных балок;

h_б- толщина слоя балласта;

b_б- ширина балластного корыта.

Коэффициенты надёжности по нагрузке _f для постоянных нагрузок при расчёте на прочность принимаются:

• для собственного веса конструкции _f1=1,1;

• для веса мостового полотна с ездой на балласте _f2=1,3.

При расчёте на прочность нормативная временная нагрузка по схеме СК используется в расчётах в виде

• эквивалентной нагрузки К кН/м, соответствующей наиболее тяжёлой нагрузке от состава с локомотивом;

• распределённой нагрузки 9,81К кН/м, от веса гружёных вагонов состава;

• нагрузки 13,7 кН/м от порожнего подвижного состава.

Нормативная временная вертикальная нагрузка на одну главную балку принимается равной р_= .

Для класса нагрузки К=11 и данных линий влияния (см. рис. 3) имеем:

р_1=100,44 кН/м ,

р_2=93,73 кН/м ,

р_3=107,15 кН/м ,

р_4=124,61 кН/м.

Нормативная временная нагрузка умножается при расчёте на прочность на коэффициент надёжности по нагрузке _f ,который принимает значения в зависимости от длины загружения линии влияния :

_f1=1,26,

_f2=1,26 ,

_f3=1,26,

_f4=1,28.

Динамический коэффициент к нагрузкам от подвижного состава определяется по формуле

1+= =1+ =1,3.

Рис.3. Линии влияния усилий в разрезной балке.

Полные усилия в сечениях разрезной балки при расчёте на прочность определятся по следующим формулам:

М₁= = =3667,93 кНм;

М₂= = =4624,7 кНм;

Q₀= = =1518,73 кН;

Q₂= = =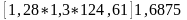349,9 кН.

Усилия при расчёте на трещиностойкость определяются от действия на конструкцию нормативных нагрузок. Коэффициенты надёжности по нагрузке в вышеприведённых формулах принимаются _f1=_f2=_f=1,0; динамический коэффициент 1+=1,0:

М₁= = =2430,54 кНм;

М₂= = =3086,92 кНм;

Q₀= = =1005,28 кН;

Q₂= = =210,28 кН.

Огибающие эпюры представлены на рис. 4.

Рис.4. Огибающие эпюры в разрезной балке.

2.2.2.Расчёт балки из обычного железобетона.

Расчёт на прочность по изгибающему моменту.

Действительную форму поперечного сечения приводим к расчётной форме (рис. 5).

Р ис. 5. Расчётная схема поперечного сечения главной балки.

Вычисляем приведённую (среднюю) толщину плиты при фактической ширине плиты b_f=2,08 м:

h_f^’= = =0,2 м.

Максимальная ширина плиты сжатой зоны тавровых и коробчатых сечений, учитываемая в расчёте, ограничена длиной свесов плиты, которая не должна быть больше 6h_f=1,86 м ; расчётная ширина плиты b_f^’ таврового сечения не должна превышать значения b_f^’ b 12h_f^’, а длина свесов плиты между соседними балками не должна быть больше 0,5(B-b); где B=1,80 м- расстояние между осями главных балок.

Действительная форма плиты переменной толщины и вутов заменяется в расчётном сечении прямоугольной формой с высотой h_f^’ и шириной b_f^’. Центр тяжести арматуры ориентировочно назначается на расстоянии a_s=0,12 м от нижней грани пояса балки. Тогда

Расчёт на прочность по изгибающему моменту производим, начиная с наиболее нагруженного сечения. Определим в первом приближении высоту сжатой зоны бетона x₁ при действии расчётного момента М₂=4624,7 кН/м: x₁=h₀- =1,035- =0,181 м.

Так как x₁=0,181 м <h_f^’=0,2 м , то из этого следует, что сечение работает как прямоугольное и необходимая площадь рабочей арматуры .

Армирование будем производить арматурой класса А-II диаметром d=40мм. Площадь поперечного сечения одного стержня равна 12,57 см². Определяем необходимое количество стержней:

n_ст = =15,6 ст. =16ст. После уточнения площади A_р = 201,12см² c учётом принятого количества арматуры находим значение x₂ (так как сечение рассчитывается как прямоугольное, то b=b_f.): x₂= = =0,18 м . Вычисляем окончательное значение

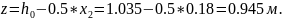
Проверяем прочность сечения по изгибающему моменту: 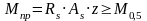_; М_пр=250*0,020*0,945*10⁶=4725,0кНм 4624,7 кНм. Проверка выполнена.

Расчет на прочность по поперечной силе.

При расчете на прочность по поперечной силе предполагается, что в предельном состоянии образуется наклонная трещина в бетоне, разделяющая элемент на две части. Поперечная сила в наклонном сечении воспринимается отогнутой арматурой, хомутами и бетоном сжатой зоны.

Места отгибов стержней рабочей арматуры согласуем с эпюрой действующих в балке изгибающих элементов. Для этого точки отгибов сносим на эпюру М, следя, чтобы предельный момент оставшихся стержней не был меньше расчетного момента в сечении. Для построения эпюры материалов используем приближенную зависимость, считая, что предельный момент, воспринимаемый сечением с одним стержнем рабочей арматуры.

М_пр = М_пр/n_ст = 4725,0/16 = 295,3125 кНм.

Проверка прочности наклонного сечения на действия наклонного сечения на действие поперечной силы производится из условия:

где Q – максимальное значение поперечной силы от внешних нагрузок, расположенных по одну сторону от наклонного сечения

R_sw = 0,8 R_s – расчетное сопротивление арматуры отогнутых стержней или хомутов (для арматуры класса A II R_s = 0.8250 = 200 МПа);

A_si и A_sw – площади поперечного сечения соответственно одного отогнутого стержня и всех ветвей одного хомута, пересекающих наклонное сечение,

- поперечное усилие, передаваемое на бетон сжатой зоны сечения;

с – длина горизонтальной проекции сечения (с = 3,61м.);

Т.о. получим:

- условие выполняется, следовательно в дальнейших расчетах принимаем Q_b= кН

Располагаем схемой, определяем по ней количество стержней, пересекающих наклонное сечение и, соответственно, суммарную площадь

Площадь всех ветвей одного хомута определяется:

где d_sw =12мм – диаметр хомутов

n_sw – число ветвей одного хомута.

Шаг хомутов a_sw принимается не более: на концевых участках с длиною равной высоте балки – 10 см; на приопорных участках до четверти длины пролета – 15 см; на среднем участке – 20 см.

При отсутствии отогнутых стержней на среднем участке балки (∑A_si=0) прочность наклонного сечения должна быть обеспечена за счет выбора соответствующего диаметра и шага хомутов.

Проверим прочность наклонного сечения при угле α=40°:

- условие выполнено.

Расчет на трещиностойкость по касательным напряжениям

Расчет по касательным напряжениям выполняют в предложении упругой работы конструкции, но без учета бетона растянутой зоны. В расчете ограничивается величина касательных напряжений, действующих по нейтральной оси сечения.

Касательные напряжения могут быть определены (приближенно) по формуле

τ=Q_i’’/bz≤1,15R_b,sh,

где Q_i’’ –поперечная сила в рассматриваемом сечении от нормативных нагрузок;

b – толщина ребра балки;

z – плечо пары внутренних сил из расчета на прочность по изгибающему моменту.

τ=180,63/0,5*94,3=3,83

1,15*3,60=4,14

3,83≤4,14 Условие выполняется.

Список используемой литературы:

1. Мосты и тоннели / Под ред. В. О. Осипова. – М.:Транспорт, 1988..

2. Расчет балочных пролетных строений железобетонных: Учеб. пособие /Э.С. Карапетов, Е.Д.Максарев. – Л.: ЛИИЖТ, 1988. – 50 с.

3. Проектирование опор мостов: Метод. указ. к курс. и дипл. проектированию. Ч.1. Конструирование опор./ Сост. В.В. Миронов, В.Н. Смирнов. – Л.: ЛИИЖТ, 1989. – 50 с.

4. Проектирование опор мостов: Метод. указ. к курс. и дипл. проектированию. Ч.2. Расчет опор./ Сост. В.Н. Смирнов, С.А. Шульман. – Л.: ЛИИЖТ, 1990. – 46 с.

5. Проектирование опор мостов: Метод. указ. к курс. и дипл. проектированию. Ч.3. Современные конструкции мостовых опор./ Сост. В.Н. Смирнов, С.А. Шульман. – СПб.: ПИИЖТ, 1992. – 35 с.

6. СНиП 2.05.03-84 «Мосты и Трубы» 1996г.