
- •Навчальна програма
- •«Автоматизовані електроприводи»
- •Цільова настанова
- •Головні цільові настанови.
- •Визначальні цільові настанови.
- •Бути ознайомленим:
- •Організаційно-методичні вказівки.
- •Тема 1. Механіка електроприводу.
- •Тема 2. Механічні і електромеханічні характеристики електроприводів.
- •Тема 3. Регулювання кутовій швидкості корабельних електроприводів.
- •Тема 4. Електричні апараті і елементі керуючих пристроїв електроприводів.
- •Тема 5. Принципи управління електроприводів.
- •Тема 6. Типові комплектні пристрої управління корабельними електроприводами.
- •Розподіл навчального часу за розділами, темами і видами навчальних занять
- •5. Інформаційно-методичне забезпечення.
- •1. Загальні відомості про електроприводи і їх класифікація
- •2. Електричні двигуни постійного струму
- •2.1. Устрій машин постійного струму.
- •2.2. Способи збудження і електричні рівняння машин постійного струму.
- •3. Електричні двигуни змінного струму
- •3.1. Устрій і основні співвідношення асинхронних двигунів.
- •3.2. Електричні рівняння і схеми асинхронного двигуна.
- •Моменти на валу двигуна й корабельного виконавчого механізму
- •2. Механічні характеристики корабельних виконавчих механізмів
- •3. Рівняння руху електропривода і його аналіз
- •4. Приведення моментів виконавчого механізму до валу двигуна
- •1. Механічні характеристики асинхронного двигуна
- •2. Механічні й електромеханічні характеристики двигуна постійного струму.
- •Електромеханічна і механічна характеристики двигуна постійного струму.
- •Гальмівні режими двигуна постійного струму.
- •3.4. Механічні характеристики в рухових і гальмівних режимах.
- •Висновки
- •План лабораторного заняття Тема: лз № 1. Дослідження механічних і електромеханічних характеристик аеп постійного струму.
- •Додаткова
- •4. Зміст лабораторного заняття та методика його проведення
- •4.1. Мета лабораторного заняття.
- •4.2. Обов’язки курсантів (слухачів) по підготовці і виконанню робіт.
- •Організація і порядок контролю і проведення заняття.
- •4.4. Вимоги до оформлення звітів і захисту результатів роботи.
- •План лабораторного заняття Тема: лз-2. Дослідження механічних і електромеханічних характеристик аеп змінного струму.
- •Додаткова
- •4. Зміст лабораторного заняття та методика його проведення
- •4.1. Мета лабораторного заняття.
- •4.2. Обов’язки курсантів (слухачів) по підготовці і виконанню робіт.
- •Організація і порядок контролю і проведення заняття.
- •4.4. Вимоги до оформлення звітів і захисту результатів роботи.
- •1. Основні показники регулювання швидкості обертання аеп.
- •2. Регулювання швидкості обертання аеп постійного струму
- •3. Регулювання швидкості обертання аеп змінного струму.
- •3.1. Регулювання асинхронного електропривода перемиканням числа полюсів.
- •Реостатне і частотне регулювання ад.
- •Висновки
- •План лабораторного заняття Тема: лз-3. Регулювання кутовій швидкості електроприводів постійного струму.
- •Додаткова
- •4. Зміст лабораторного заняття та методика його проведення
- •4.1. Мета лабораторного заняття.
- •4.2. Обов’язки курсантів (слухачів) по підготовці і виконанню робіт.
- •Організація і порядок контролю і проведення заняття.
- •4.5. Вимоги до оформлення звітів і захисту результатів роботи.
- •План лабораторного заняття Тема: лз-4. Регулювання кутовій швидкості електроприводів змінного струму.
- •Додаткова
- •4. Зміст лабораторного заняття та методика його проведення
- •4.1. Мета лабораторного заняття.
- •4.2. Обов’язки курсантів (слухачів) по підготовці і виконанню робіт.
- •Організація і порядок контролю і проведення заняття.
- •4.5. Вимоги до оформлення звітів і захисту результатів роботи.
- •Введення
- •1. Призначення й класифікація апаратів й елементів керуючих пристроїв аеп
- •2. Основи побудови й принцип дії контактно-релейних апаратів
- •2.1. Основні системи електромагнітних апаратів.
- •2.2. Способи гасіння електричної дуги в дугагасильних системах апаратів
- •3. Основні характеристики електромагнітних апаратів
- •Введення
- •1. Порядок побудови й читання електричних схем керування аэп.
- •1.1. Зображення й позначення елементів електричних схем.
- •1.2. Зображення й позначення принципових електричних схем керування аэп.
- •2. Принципи автоматизації пуску, реверса й захисту аеп.
- •2.1. Принципи автоматизації пуску двигунів постійного струму.
- •Автоматизація режимів гальмування й реверсу двигунів.
- •Автоматизація режимів захисту двигунів.
- •План практичного заняття Тема: пз № 1. Побудова і експлуатація електричної контактної і безконтактної апаратурі управління електроприводами.
- •Навчальни питання і розподіл часу
- •4. Зміст практичного заняття та методика його проведення
- •4.1. Мета практичного заняття.
- •4.2. Обов’язки курсантів (слухачів) по підготовці і участі в заняттях.
- •Організація і порядок контролю і проведення заняття.
- •4.5. Підведення підсумків практичного заняття.
- •План практичного заняття
- •Навчальни питання і розподіл часу
- •4. Зміст практичного заняття та методика його проведення
- •4.1. Мета практичного заняття.
- •4.2. Обов’язки курсантів (слухачів) по підготовці і участі в заняттях.
- •Організація і порядок контролю і проведення заняття.
- •4.5. Підведення підсумків практичного заняття.
- •Введення
- •1. Управління аеп постійного струму за допомогою магнітних пускачів і станцій.
- •1.1. Принципи пуску двигуна у функції ерс і струму.
- •1.2. Принципи пуску двигуна у функції часу.
- •1.3. Електричні схеми корабельних пускачів і станцій постійного струму.
- •2. Управління аеп змінного струму за допомогою магнітних пускачів
- •2.1. Принципи управління аеп змінного струму.
- •2.2. Електричні схеми безконтактних пускачів змінного струму.
- •Висновки
- •Введення
- •Керування аеп за допомогою силових кулачкових контролерів
- •Керування аэп за допомогою магнітних контролерів.
- •3. Керування аеп за допомогою тиристорних контролерів.
- •Висновки
- •План семінарського заняття
- •Додаткова
- •Методичні вказівки курсантам (слухачам) щодо підготовки до семінарського заняття
- •План практичного заняття
- •Навчальни питання і розподіл часу
- •4. Зміст практичного заняття та методика його проведення
- •4.1. Мета практичного заняття.
- •4.2. Обов’язки курсантів (слухачів) по підготовці і участі в заняттях.
- •Організація і порядок контролю і проведення заняття.
- •4.5. Підведення підсумків практичного заняття.
- •План практичного заняття
- •Навчальни питання і розподіл часу
- •4. Зміст практичного заняття та методика його проведення
- •4.1. Мета практичного заняття.
- •4.2. Обов’язки курсантів (слухачів) по підготовці і участі в заняттях.
- •Організація і порядок контролю і проведення заняття.
- •4.5. Підведення підсумків практичного заняття.
- •Контрольні питання
- •Література
1. Механічні характеристики асинхронного двигуна
Вивід механічної характеристика асинхронного двигуна. Асинхронні двигуни одержали досить широке застосування на кораблях й у промисловості завдяки ряду істотних переваг у порівнянні з іншими типами двигунів. Асинхронний двигун простий і надійний в експлуатації, тому що не має колектора; асинхронні двигуни дешевше й значно легше двигунів постійного струму.
Асинхронна машина може працювати в режимах двигуна, генератора й електромагнітного гальма. Ковзання асинхронної машини
у зазначених режимах змінюється в наступних межах:
- при руховому режимі:
- при генераторному режимі:
- при гальмовому режимі:
Величина ковзання в режимі холостого ходу близька до нуля, але ніколи нулю не рівняється, оскільки при s = 0 струми в роторі й обертаючи моменті зникають. У номінальному руховому режимі s = 0,01 - 0,06. Ковзання асинхронного двигуна виражають як в абсолютних значеннях, так й у відсотках.
Рівняння механічної характеристики асинхронного двигуна доцільно шукати у вигляду залежності його електромагнітного моменту від ковзання М = f(S). Для виводу рівняння механічної характеристики асинхронного двигуна можна скористатися спрощеною схемою його заміщення, наведеної на рис. 3.1, де прийняті наступні позначення:
— первинна фазна напруга;
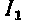 —
фазний струм статора;
—
фазний струм статора;
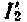 —
наведений струм ротора;
—
наведений струм ротора;
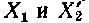 — первинний
й вторинний реактивний опор розсіювання;
— первинний
й вторинний реактивний опор розсіювання;
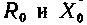 — активний і
реактивний опори
контуру намагнічування;
— активний і
реактивний опори
контуру намагнічування;
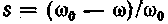 — ковзання
двигуна;
— ковзання
двигуна;
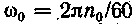 -
синхронна кутова швидкість
двигуна (
-
синхронна кутова швидкість
двигуна (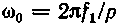 ;
;
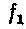 —
частота мережі; р —
число пар полюсів);
—
частота мережі; р —
число пар полюсів);
 — первинний
й вторинний активний опор.
— первинний
й вторинний активний опор.
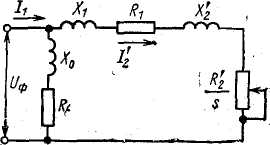
Рис. 3.1. Спрощена схема заміщення асинхронного двигуна.
Відповідно до наведеної схеми заміщення можна одержати вираження для вторинного струму ротора:
![]()
Момент
асинхронного двигуна може бути визначений
з
вираження втрат
![]() ,
звідки
,
звідки
![]()
З
урахуванням раніше отриманого значення
струму
![]() ,
одержуємо механічну характеристику
АД:
,
одержуємо механічну характеристику
АД:
![]()
Крива
моменту у функції ковзання
![]() має два максимуми:
один — у генераторному режимі, іншої —
у руховому.
має два максимуми:
один — у генераторному режимі, іншої —
у руховому.
Дорівнюючи
![]() ,
визначаємо значення критичного ковзання
,
визначаємо значення критичного ковзання
![]() ,
при якому двигун розвиває максимальний
(критичний) момент
,
при якому двигун розвиває максимальний
(критичний) момент
![]()
При значних опорах роторного ланцюга максимум моменту може виявитися в режимі гальмування проти включенням.
Підставляючи значення критичного ковзання у вираз для моменту, находимо вираження для максимального моменту
![]()
Знак
«+» у двох останніх рівностях ставиться
до рухового
режиму (або гальмуванню проти включенням),
знак «—» до генераторного
режиму роботи паралельно з
мережею (при
![]() ), рис. 3.2.
), рис. 3.2.
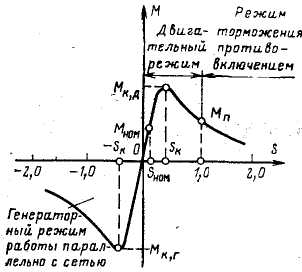
Рис. 3.2. Механічна характеристика асинхронного двигуна.
Для практичних розрахунків після відповідного перетворення механічної характеристики АД можна одержати рівняння Клоса:
![]()
де
![]() —
максимальний момент двигуна; Sк
— критичне
ковзання, що відповідає
максимальному моменту;
а =
R1/R2΄.
—
максимальний момент двигуна; Sк
— критичне
ковзання, що відповідає
максимальному моменту;
а =
R1/R2΄.
Тут варто підкреслити: досить важливе для практики обставину - вплив зміни напруги мережі на механічні характеристики асинхронного двигуна. Як видно з (3.36), при даному ковзанні момент двигуна пропорційний квадрату напруги, тому двигун цього типу дуже чутливий до коливань напруги мережі. При цьому критичне ковзання й кутова швидкість ідеального холостого ходу не залежать від напруги.
Аналіз механічної характеристики асинхронного двигуна. На рис. 3.2 наведена механічна характеристика асинхронного двигуна. Її характерні точки:
1)
![]() ,
при цьому швидкість двигуна дорівнює
синхронної;
,
при цьому швидкість двигуна дорівнює
синхронної;
2)
![]() ,
що відповідає номінальній швидкості
й номінальному моменту;
,
що відповідає номінальній швидкості
й номінальному моменту;
3)
![]() — максимальний момент
у руховому
режимі;
— максимальний момент
у руховому
режимі;
4)
![]() — початковий пусковий
момент;
— початковий пусковий
момент;
5)
![]() — максимальний момент
у генераторному режимі роботи паралельно
з мережею.
— максимальний момент
у генераторному режимі роботи паралельно
з мережею.
При
![]() двигун
працює в режимі гальмування
проти
включенням, при
двигун
працює в режимі гальмування
проти
включенням, при
![]() має
місце генераторний режим
роботи паралельно з мережею.
має
місце генераторний режим
роботи паралельно з мережею.
Необхідно підкреслити, що абсолютні значення ковзання S у руховому й генераторному режимах паралельно з мережею однакові.
Однак максимальні моменти в руховому й генераторному режимах різні. У генераторному режимі роботи паралельно з мережею максимальний момент за абсолютним значенням більше, що видно зі співвідношення
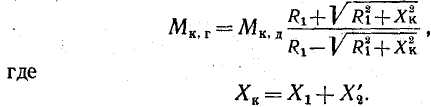
Якщо в рівнянні Клоса зневажити активним опором статора, то вийде широко відома формула Клоса, більше зручна для розрахунків:
![]()
тут
![]() .
.
Позначивши
кратність максимального
момент
![]() через перевантажувальну
спроможність
через перевантажувальну
спроможність
![]() , одержимо:
, одержимо:
![]()
В останнім вираженні перед знаком кореня для двигуна варто брати знак «+».
Аналіз
формули Клоса показує, що при великих
ковзаннях
![]() (неробоча
частина характеристики) вийде рівняння
гіперболи, якщо в
цьому випадку зневажити другим членом
знаменника, тобто
(неробоча
частина характеристики) вийде рівняння
гіперболи, якщо в
цьому випадку зневажити другим членом
знаменника, тобто
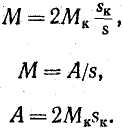
Ця частина характеристики практично відповідає лише пусковим і гальмівним режимам.
При
малих значеннях ковзання
![]() для
для![]()
![]() вийде
рівняння прямої, якщо зневажити першим
членом у знаменнику:
вийде
рівняння прямої, якщо зневажити першим
членом у знаменнику:

Ця лінійна частина характеристики є її робочою частиною, на якій двигун звичайно працює в сталому режимі. На цій же частині характеристики перебувають точки, що відповідають номінальним даним двигуна:
![]()
Статичне
падіння (перепад) швидкості у відносних
одиницях на природній механічній
характеристиці асинхронного
двигуна при номінальному моменті
визначається
його номінальним ковзанням.
Номінальне ковзання залежить від опору
ротора.
Найменшим номінальним ковзанням при
однаковій
потужності й числі полюсів володіють
звичайно двигуни
з короткозамкненим ротором нормального
виконання. У цих
двигунів у силу конструктивних
особливостей
опір ротора має відносно невелике
значення, що веде до зменшення значень
критичного ковзання
![]() і номінального ковзання
і номінального ковзання
![]() .
По
тим ж причинам при збільшенні потужності
двигуна зменшується
його номінальне ковзання й росте
жорсткість
природної характеристики.
.
По
тим ж причинам при збільшенні потужності
двигуна зменшується
його номінальне ковзання й росте
жорсткість
природної характеристики.
