Контрольные задания Вариант 1

1. В кошельке 8 монет: одна - 15 коп., три по 10 коп., три по 5 коп. и одна - 1 коп. Вынимают две монеты. Найти вероятность того, что в сумме будет меньше 17 копеек.

2. Из колоды в 52 карты 6 раз извлекают по одной карте (каждый раз карту возвращают в колоду). Что вероятнее: 3 раза извлечь карту красной масти или два раза извлечь туз?

3. Из полного набора домино извлекают одну кость. Найти распределение, среднее и дисперсию числа очков на этой кости.

4. Известна дифференциальная функция распределения:

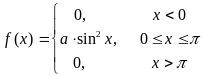
Требуется найти неизвестный коэффициент а, вычислить математическое ожидание, дисперсию, вероятность попадания X в интервал (0,/2), построить графики интегральной и дифференциальной функций.

5. Считая, что X - нормально распределенная случайная величина, которая задается функцией плотности распределения 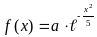, найти a, M(X), D(X), P(X-M(X)<2).

Вариант 2

1. На 10 карточках написаны числа от 0 до 9. Последовательно вытягивают 3 карточки. Найти вероятность того, что полученное число будет больше 300 и четное.

2. Один преподаватель принимает зачет с положительным исходом с вероятностью 0.8, а другой с вероятностью 0.4. Студент знает, что его шансы попасть ко второму преподавателю 0.7. Найти вероятность того, что студент сдаст зачет.

3. В ящике 3 белых и 5 черных шариков. Из ящика последовательно извлекают 4 раза по одному шарику и запоминают его цвет (каждый раз шарик возвращают обратно). Найти распределение, среднее и дисперсию числа белых шариков.

4. Известна дифференциальная функция распределения:

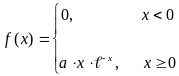
Требуется найти неизвестный коэффициент а, вычислить математическое ожидание, дисперсию, вероятность попадания X в интервал (0,1), построить графики интегральной и дифференциальной функций.

5. Считая, что X - нормально распределенная случайная величина, которая задается функцией плотности распределения 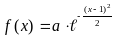, найти a, M(X), D(X), P(-0.5<X<2.5).

Вариант 3

1. Найти вероятность того, что при размещении семи различных шаров по десяти большим различным ящикам ровно 4 ящика останутся пустыми.

2. Фальшивую монету (вероятность выпадения "герба" - 0.6) бросают 8 раз. Найти вероятность того, "герб" выпадает более двух раз.

3. Одновременно бросают игральную кость и монету, если на монете выпал "герб", то к сумме очков на кости прибавляют 2. Найти распределение, среднее и дисперсию числа очков, выпавших в результате эксперимента

4. Известна дифференциальная функция распределения:

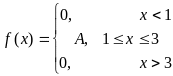
Требуется найти неизвестный коэффициент A, вычислить математическое ожидание, дисперсию, вероятность попадания X в интервал (1,2), построить графики интегральной и дифференциальной функций.

5. Считая, что X - нормально распределенная случайная величина, которая задается функцией плотности распределения 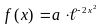, найти a, M(X), D(X), P(X>3).

Вариант 4

1. На 10 карточках написаны числа от 0 до 9. Последовательно вынимают 3 карточки и укладывают в ряд. Найти вероятность того, что полученное таким образом число делится на 20.

2. Каждое утро экстрасенс, выходя из дому, бросает монету. Если выпадет "герб", то он берет с собой зонтик, иначе выходит без него. При этом, если он выходит из дома с зонтом, то дождь идет с вероятностью 0.3, а если без зонта - то с вероятностью 0.8. Найти вероятность того, что он попадет под дождь.

3. Из колоды в 52 карты наугад извлекают 3 карты. Найти распределение, среднее и дисперсию числа извлеченных тузов.

4. Известна дифференциальная функция распределения:

Требуется найти неизвестный коэффициент а, вычислить математическое ожидание, дисперсию, вероятность попадания X в интервал (0,3), построить графики интегральной и дифференциальной функций.

5. Считая, что X - нормально распределенная случайная величина, которая задается функцией плотности распределения , найти a, M(X), D(X), P(0<X<5).