- •Кафедра «Математики»
- •§ 1. Предмет теории вероятностей
- •§ 2. Случайные события
- •Так как , то , каково бы ни было по своей природе событие а.
- •Если а - событие невозможное, то .
- •Если в- событие достоверное, то .
- •§ 3. Случайные величины и их характеристики
- •Контрольные задания Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Литература
- •Редактор и.Х. Эмиров Корректор и.Ю. Трапезникова
§ 3. Случайные величины и их характеристики
Число мальчиков, которые родятся в ближайший день в каком-то населенном пункте, может быть различным. Оно может быть равным 0 (не родится ни одного мальчика), 1, 2 и т.д. до некоторого конечного числа n. К такого же типа величинам относятся: вес корнеплода свеклы на участке; дальность полета артиллерийского снаряда; количество бракованных деталей в партии и т.д. Общим для них является то, что каждая может принимать некоторые значения, но нельзя достоверно предсказать, какое именно значение она примет в рассматриваемом опыте, явлении, наблюдении. Эти величины характеризуют все возможные результаты опыта или наблюдения с количественной стороны.
Случайной называется величина, которая в результате испытания может принять то или иное числовое значение, причем заранее неизвестно, какое именно.
Случайная величина называется дискретной (прерывной), если все ее возможные значения изолированы друг от друга и их можно перенумеровать.
Случайная величина называется непрерывной, если все ее возможные значения заполняют некоторый конечный или бесконечный интервал.
Случайные величины обозначаются заглавными буквами латинского алфавита X, Y, Z, а их возможные значения - соответствующими малыми буквами, то есть x1, x2,..., xn и т.д.
Для каждого их значений случайной величины указывают его вероятность. Сумма этих вероятностей должна быть равна 1.
Законом распределения случайной величины называется соответствие, устанавливающее связь между возможными значениями случайной величины и их вероятностями.
Закон распределения может быть задан:
аналитически;
таблично;
графически.
Пример. Отмечено, что в некоторой местности в течение ряда лет в июне 30% дождливых дней. Составить закон распределения случайной величины X - числа дождливых дней в течение одной недели июня месяца. События, состоящие в том, что в 1-й день недели идет дождь, во 2-й - дождь и т.д. считать независимыми.
Решение. Случайная величина X принимает следующие значения:
x1=0, x2=1, x3=2, x4=3, x5=4, x6=5, x7=6, x8=7.
Вероятности этих значений вычислим по формуле Бернулли:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Закон распределения представим в виде таблицы
X |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
pi |
0.0824 |
0.2472 |
0.3128 |
0.2263 |
0.0973 |
0.0250 |
0.0036 |
0.0002 |
Наибольшую вероятность имеет событие, состоящее в том, что на неделе будет два дождливых дня.
Иначе закон распределения называют рядом распределения.
Однако
не все случайные величины могут быть
описаны так просто как дискретные
случайные величины. Например, время
горения электрической лампочки может
принимать любое значение от нуля до
бесконечности. И если предполагается,
что лампочка была в начале исправной,
то вероятность того, что время ее службы
будет в точности равно некоторому
значению, будет равно нулю. Ненулевыми
будут вероятности только сложных
событий: например, что время службы
лампочки от одного до двух месяцев. В
этом случае табличный способ задания
случайных величин не применим и
распределение случайной величины
полностью определяется ее функцией
распределения
![]() ,
то есть функция распределения в точке
x
- это вероятность того, что случайная
величина X
примет значение, меньшее заданного
числа x.
,
то есть функция распределения в точке
x
- это вероятность того, что случайная
величина X
примет значение, меньшее заданного
числа x.
Из определения следуют следующие свойства:
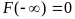 ;
; ;
; -
неубывающая функция;
-
неубывающая функция;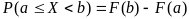 -
вероятность попадания в интервал.
-
вероятность попадания в интервал.
Исходя из определения функции распределения можно дать другое определение непрерывной случайной величины: случайная величина, принимающая вещественные значения, называется непрерывной, если непрерывна ее функция распределения.
Нагляднее
всего непрерывную
случайную величину
можно представить тогда, когда ее функция
распределения не только непрерывна, но
и дифференцируема (за исключением, может
быть, конечного числа точек). В этом
случае вероятности связанных с данной
случайной величиной событий можно
выразить через посредство так называемой
функции
плотности вероятности, которая
является производной от функции
распределения. Ее обозначение
![]() .
Часто по условию задачи задают именно
плотность распределения, зная которую
можно вычислить и (интегральную) функцию
распределения (по формуле Ньютона-Лейбница):
.
Часто по условию задачи задают именно
плотность распределения, зная которую
можно вычислить и (интегральную) функцию
распределения (по формуле Ньютона-Лейбница):
![]() .
.
Согласно второму свойству F(x) имеем
![]() .
.
Последнее равенство называется условием нормировки f(x).
Пример. Плотность распределения случайной величины X равна
![]() .
.
Найти A, F(x) и вероятность P(0.5X1.5).
Решение. Для нахождения А запишем условие нормировки

Если
x<0,
то
![]() .
.
Если
![]() ,
то
,
то
![]()
Если
x>2,
то
![]() .
.
Итак,
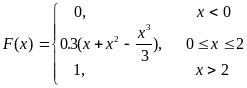 .
.
Наконец, P(0.5X1.5)=P(X<1.5)+P(X=1.5)-P(X<0.5)=F(1.5)+0-F(0.5)=
![]()
Составить полное представление о случайной величине только по закону распределения часто бывает трудно. Поэтому возникает необходимость характеризовать случайную величину с помощью некоторых постоянных величин. Они должны получаться на основе ее закона распределения.
Математическое ожидание - важнейшая «характеристика положения» случайной величины. Для дискретной величины она вычисляется по формуле
![]() ,
,
где x1, x2,...,xn,... - возможные значения случайной величины, p1, p2,,...,pn,...- их вероятности.
Математическое ожидание - это число, которое выражает среднее значение случайной величины по распределению.
Отметим свойства математического ожидания:
M(C)=C
M(CX)=CM(X)
M(X+Y)=M(X)+M(Y)
M(XY)=M(X)M(Y) (для независимых случайных величин).
Еще одной важной характеристикой случайной величины является дисперсия. Для дискретной величины она определяется по формуле
![]() .
.
При практических вычислениях используют формулу
![]() .
.
Дисперсия характеризует меру рассеяния возможных значений случайной величины около ее математического ожидания. Из двух величин с равными математическими ожиданиями та считается «лучшей», которая имеет меньший разброс.
Свойства дисперсии:
D(C)=0
D(CX)=C2D(X)
D(XY)=D(X)+D(Y) (для независимых случайных величин).
Корень квадратный из дисперсии случайной величины называется средним квадратическим отклонением и обозначается (X) или x:
![]() .
.
Пример. Случайная величина X распределена по следующему закону:
X |
1 |
2 |
3 |
P(X) |
0.2 |
0.3 |
0.5 |
Найти M(X) и D(X).
Решение.
M(X)=10.2+20.3+30.5=2.3.
Для вычисления дисперсии составим закон распределения X2:
X |
1 |
4 |
9 |
P(X) |
0.2 |
0.3 |
0.5 |
M(X2)=10.2+40.3+90.5=5.9.
=5.9-(2.3)2=0.61.
Для непрерывных случайных величин математическое ожидание и дисперсия определяются формулами
![]() ,
,
![]() .
.
Вычислительная формула для D(X):
![]() .
.
Для случайных величин существует несколько наиболее распространенных распределений, характеристики которых приведены в таблице.
Сводная таблица характеристик законов распределения случайных величин
Вид случай-ной |
№ пп |
Наиме-нование |
Область значений |
Вероятность |
Плот-ность |
Числовые характеристики |
Интегральная |
||
величи-ны |
|
закона |
СВ |
пара-метров |
P(X) |
f(x) |
M(X) |
D(X) |
функция F(x) |
Дискрет- ные |
Д1 |
Геомет-рический |
m= 1,2,3,... |
0<p<1 |
|
-- |
|
|
|
Дискрет- ные |
Д2 |
Биноми-нальный |
n= 0,1,...N |
0<p<1 N=1,2,... |
|
-- |
Np |
Npg |
|
Дискрет- ные |
Д3 |
Пуассона |
k= 0,1,2,... |
>0 |
|
-- |
|
|
|
Непре- рывные |
Н1 |
Равно-мерный (прямо-угольный) |
(a;b) |
-<b<+ a<b |
-- |
|
|
|
|
Непре- рывные |
Н2 |
Экспонен-циальный (показа-тельный) |
(0;) |
>0 |
-- |
|
|
|
|
Непре- рывные |
Н3 |
Нор-мальный (Гаусса) |
(-;+) |
>0 -<a<+ |
-- |
|
a |
2 |
|
Обратим особое внимание на нормально распределенные случайные величины.
В 1718 в Лондоне вышла в свет книга «Учение о случаях». Ее автор - французский математик А.Муавр (1667-1754). Самое большое его достижение - открытие закономерности, которая очень часто наблюдается в случайных явлениях. Он первым заметил и теоретически обосновал роль «нормального» распределения.
А.Муавр измерил рост у 1375 случайно выбранных женщин. Колоколообразная кривая (см. рисунок), которая приближенно «накрывает» диаграмму распределения роста, близка к графику функции
![]() ,
,
где

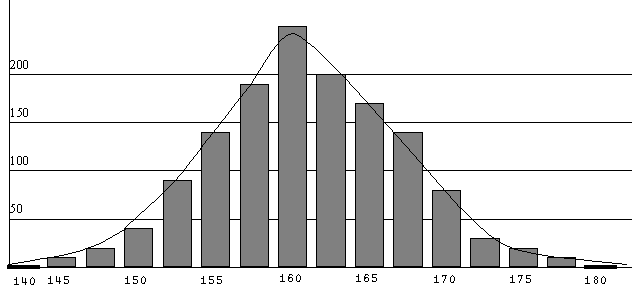
Рис. Распределение показателя роста
В
общем случае для нормального закона
![]() ,
где
,
где
![]() .
Дисперсия же вычисляется по формуле
.
Дисперсия же вычисляется по формуле
![]() .
.
Пример. Случайная величина X распределена по нормальному закону
![]() .
.
Найти P(-3<X<3).
Решение. По 4-му свойству функции распределения имеем
P(-3<X<3)=F(3)-F(-3)=
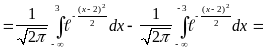
= .
.
Этот интеграл не вычисляется в элементарных функциях, его численное значение находится по таблицам (см. стр.13).
Так как
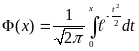 ,
,
то следует
![]() ,
,
где a и - параметры нормального закона.
Таким образом, для данного примера получаем:
![]()
Закон нормального распределения имеет важное практическое значение. Оказывается, что так распределяется скорость газовых молекул, вес новорожденных и много других случайных событий физической и биологической природы. Для этих величин характерным является то, что на их формирование влияет большое число факторов, причем влияние каждого из них мало и ни один фактор не имеет значительного преимущества перед другими.