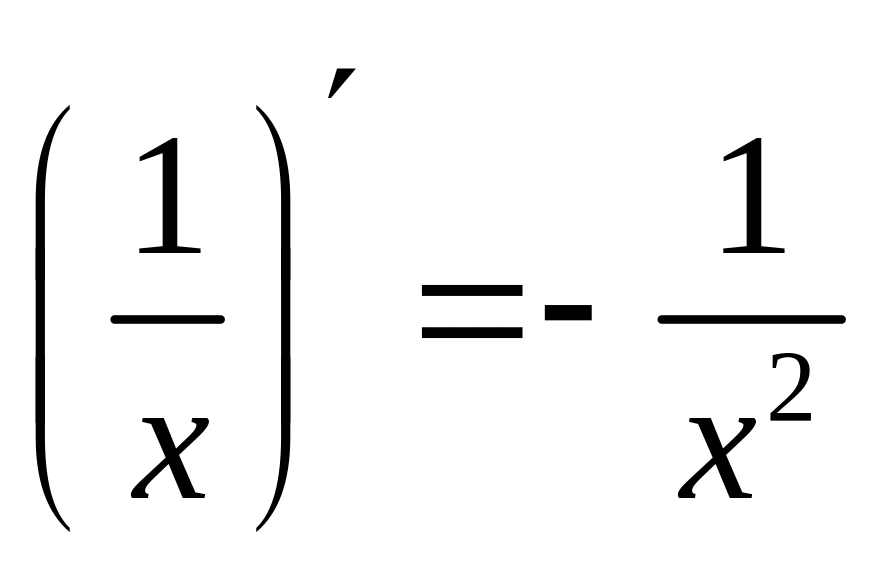8 Производная функции.
Производной функции называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):
.
Производная
функции имеет несколько обозначений:
,
,
.
Иногда в обозначении производной
используется индекс, указывающий, по
какой переменной взята производная,
например,
.
Нахождение производной функции называется дифференцированием этой функции.
Таблица производных основных элементарных функций
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример
8.1. Найти
производные функций: а) 
,
б) 
.
Решение.
а)
– степенная функция. Используя формулу
производной для степенной функции,
получим
.
б)
– показательная функция. Используя
формулу производной для показательной
функции, получим
.
Основные правила дифференцирования:
1. Производная
постоянной равна нулю, т.е.
.
2. Производная
алгебраической суммы конечного числа
дифференцируемых функций равна такой
же сумме производных этих функций,
т.е.
.
3. Производная
произведения двух дифференцируемых
функций равна произведению первого
сомножителя на второй плюс произведение
первого сомножителя на производную
второго, т.е.
.
Следствие.
Постоянный множитель можно выносить
за знак производной
.
4. Производная
частного двух дифференцируемых функций
может быть найдена по формуле
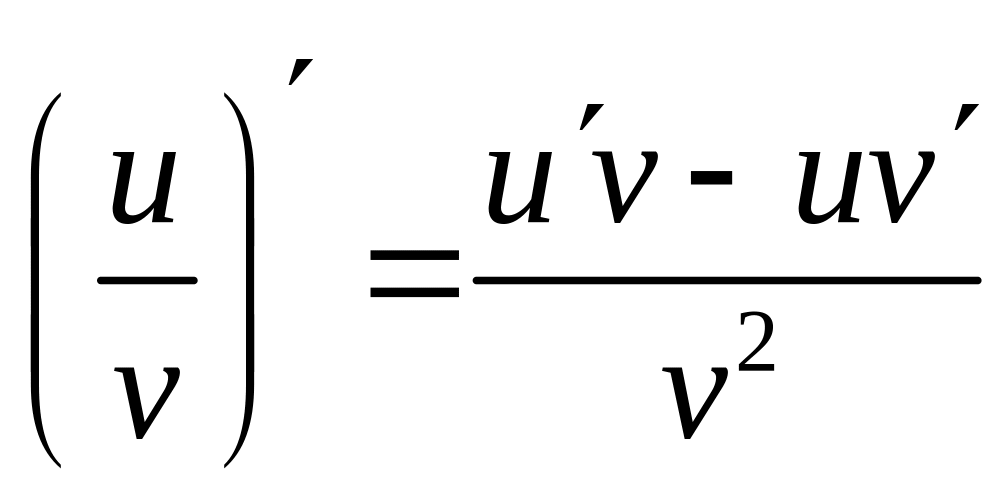
Пример
8.2. Найти
производные функций: а) 
,
б) 
,
в) 
.
Решение.
а) По
правилу дифференцирования суммы двух
функций, получим
.
б) По
правилу дифференцирования произведения
двух функций, получим
.
в) б) По
правилу дифференцирования частного
двух функций, получим
.
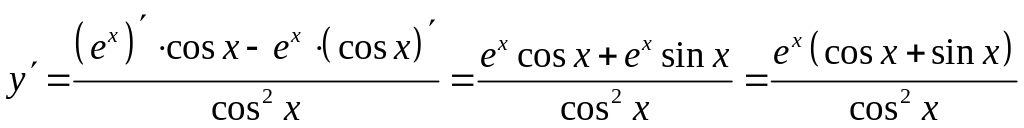Пусть
переменная
есть функция от переменной
,
а переменная
в свою очередь есть функция от независимой
переменной
,
т.е. задана сложная функция
.
Теорема.
Если
и
– дифференцируемые функции от своих
аргументов, то производная сложной
функции существует и равна производной
данной функции по промежуточному
аргументу и умноженной на производную
самого промежуточного аргумента по
независимой переменной
,
т.е.
.
Пример
8.3. Найти
производные функций: а) 
,
б) 
,
в) 
.
Решение.
а) Функцию
можно представить в виде
,
где
,
тогда
.
б) Имеем
,
где
,
тогда
.
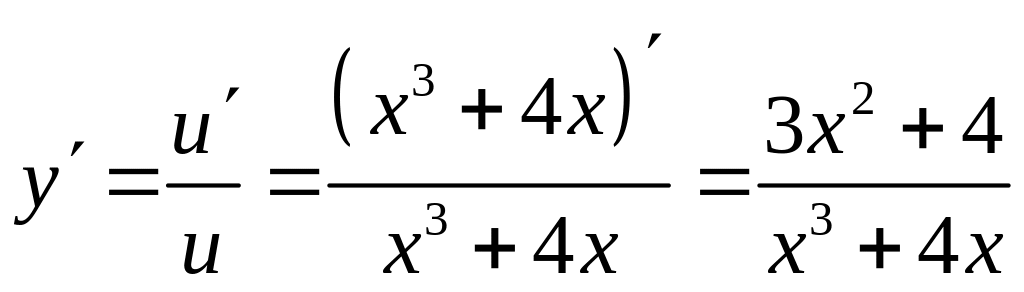в) Имеем
,
где
,
тогда
.
Производная сама является функцией, которая также может иметь производную. Производной порядка называется производная от производной порядка.
Пример
8.4. Найти
производную второго порядка от функции
.
Решение.
Дифференцируя данную функцию, получим
.
Дифференцируя производную
,
найдем вторую производную
.
9. Дифференциал функции.
Дифференциалом
функции называется главная, линейная
относительно
часть приращения функции, равная
произведению производной на приращение
независимой переменной
.
Дифференциал
независимой переменной равен приращению
этой переменной. Поэтому формулу для
дифференцирования функции можно записать
в виде
,
откуда
.
Пример
9.1. Найти
дифференциал функции
.
Решение.
Дифференциал функции
.
Дифференциалом
второго порядка
(или вторым дифференциалом)
функции
называется дифференциал от дифференциала
первого порядка этой функции, т.е.
.
Аналогичного
дифференциалом
порядка (или
дифференциалом)
называется дифференциал от дифференциала
порядка этой функции, т.е.
.
Итак,
по определению
.
Найдем выражение второго дифференциала
функции
.
Так как
не зависит от
,
то при дифференцировании считаем
постоянным:
,
т.е.
.
Аналогично, выражение
дифференциала функции имеет вид
.
Пример
9.2. Найти
,
если
.
Решение.
Так как
,
,
то
.