17. Степенные ряды.

Ряд вида называется степенным рядом. Числа , , , …, , … называются коэффициентами степенного ряда.

Придавая различные числовые значения, будем получать различные числовые ряды, которые могут оказаться сходящимися или расходящимися. Множество тех значений , при которых ряд сходится, называется областью его сходимости.

Структура области сходимости степенного ряда устанавливается с помощью теоремы Абеля.

Теорема. Если степенной ряд сходиться при значении , то он сходиться и, притом абсолютно при всех значениях таких, что .

Следствие. Если степенной ряд расходиться при значении , то он расходиться при всех значениях таких, что .

Из теоремы Абеля следует, что если есть точка сходимости ряда, то интервал весь состоит из точек сходимости данного ряда, при всех значениях вне этого интервала ряд расходиться.

	ряд сходиться
ряд расходиться		ряд расходиться

Интервал называют интервалом сходимости степенного рада. Положив интервал сходимости можно записать в виде . Число называют радиусом сходимости степенного ряда, т.е. – это такое число, что при всех , для которых ряд абсолютно сходиться, а при ряд расходиться.

Отметим, что на концах интервала сходимости (т.е. при и при ) сходимость ряда проверятся в каждом случае отдельно.

Рассмотрим степенной ряд . Радиус сходимости данного ряда можно определить по формуле 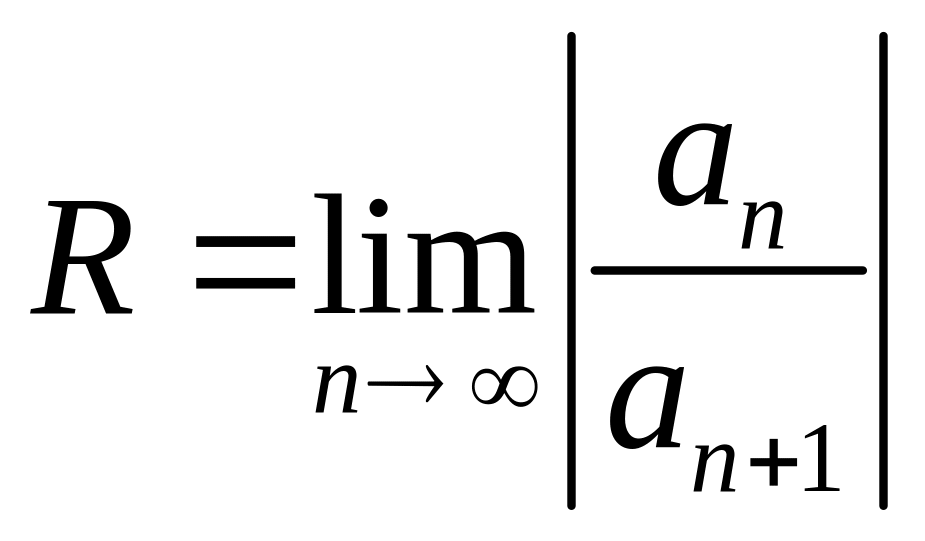. Отметим, что если ряд сходится на всей числовой прямой, то , если ряд сходится только при , то .

Пример 17.1. Найти область сходимости степенного ряда .

Решение. Так как , , то радиус сходимости равен 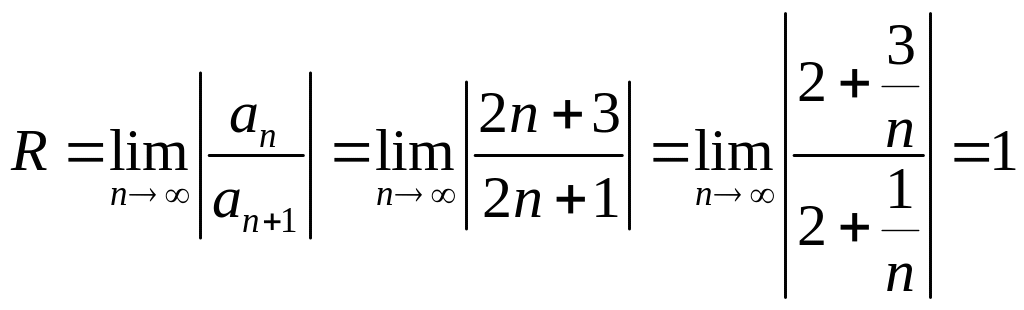. Интервал сходимости ряда . Исследуем поведение ряда на концах интервала сходимости.

При данный степенной ряд принимает вид 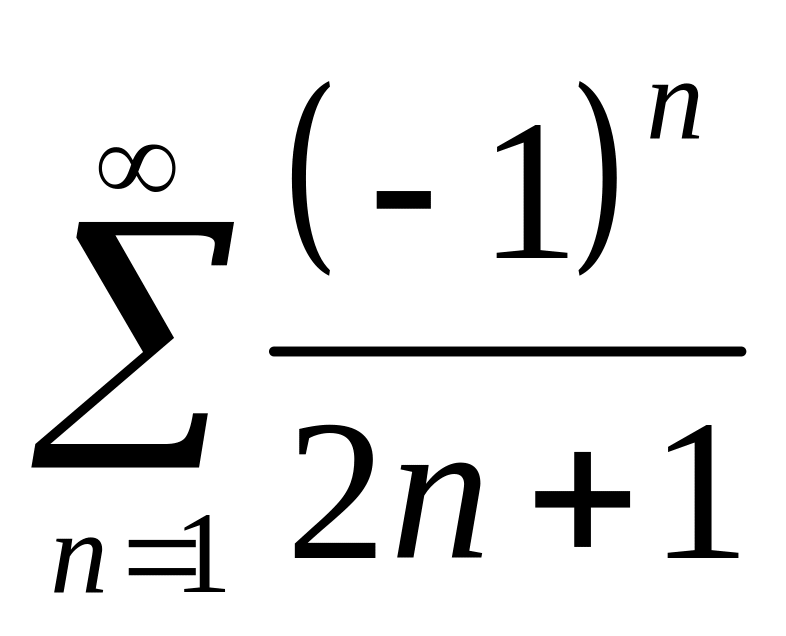. Исследуем знакочередующийся ряд по признаку Лейбница. Так как элементы знакочередующегося ряда убывают по абсолютной величине , и предел общего элемента , следовательно, ряд сходится.

При данный степенной ряд принимает вид . Сравним данный ряд с гармоническим рядом , у которого . Так как 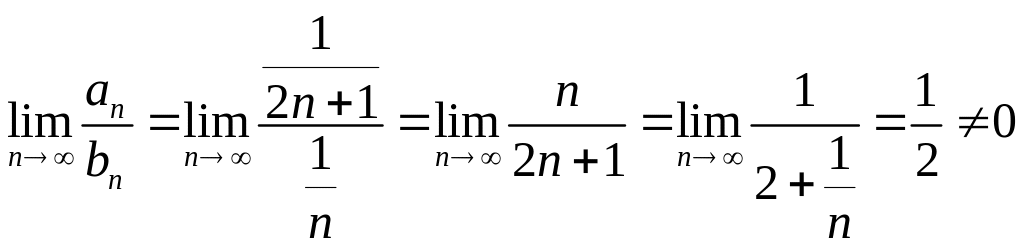, то исследуемый ряд расходится, так как расходится ряд .

Итак, область сходимости ряда .

Рассмотрим ряд . Радиус сходимости ряда, заданного по степеням , находиться по формуле , интервал сходимости определяется из условия или .

Пример 17.2. Найти радиус и интервал сходимости степенного ряда .

Решение. Радиус сходимости степенного ряда равен 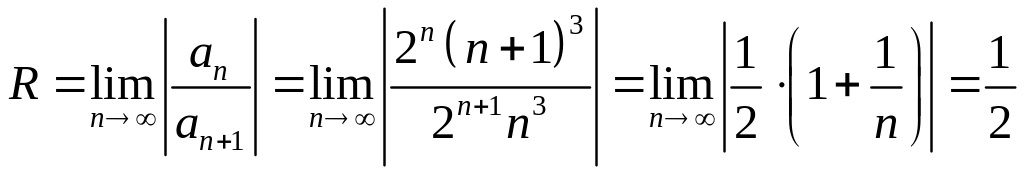. Интервал сходимости ряда есть или . Выясним поведение ряда на концах интервала сходимости.

При данный степенной ряд принимает вид 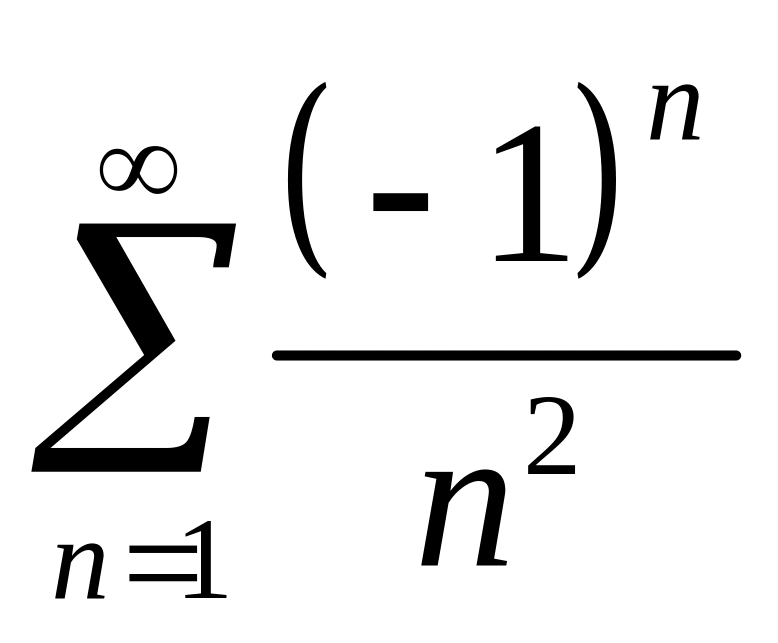. Исследуем знакочередующийся ряд по признаку Лейбница. Элементы знакочередующегося ряда убывают по абсолютной величине , и предел общего элемента , следовательно, ряд сходится.

При данный степенной ряд принимает вид . Ряд является обобщенным гармоническим рядом, следовательно, он сходится

Итак, область сходимости ряда .