2 Электрическая энергия, мощность. Законы Кирхгофа. Методы расчета электрических цепей.

Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа. Законы Кирхгофа имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач.

Первый закон Кирхгофа вытекает из закона сохранения заряда. Он состоит в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю.

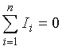
где – число токов, сходящихся в данном узле.

Например, для узла электрической цепи (рис. 1) уравнение по первому закону Кирхгофа можно записать в виде I1 - I2 + I3 - I4 + I5 = 0

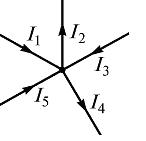
Рис. 1

В этом уравнении токи, направленные к узлу, приняты положительными.

Второй закон Кирхгофа:алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре

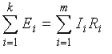
где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii, Ri – ток и сопротивление i-й ветви.

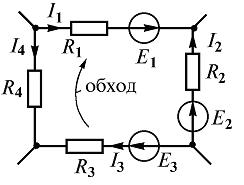
Рис. 2

Так, для замкнутого контура схемы (рис. 2) Е1 - Е2 + Е3 = I1R1 - I2R2 + I3R3 - I4R4

Методы расчета элек-х цепей

Метод узловых потенциалов

Пронумеруем узлы, потенциал в узле 3 приравняем к 0 (следовательно и потенциал в узле 4 будет равен 0) расставим токи в ветвях (от предполагаемого узла с большим потенциалом к меньшему). 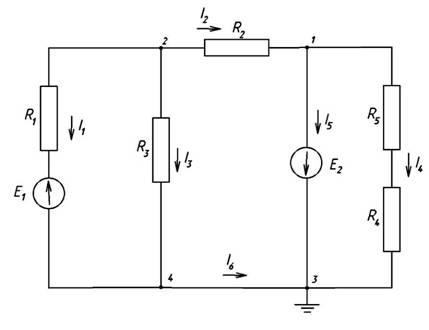  2. Поскольку потенциалы в узлах 3 и 4 известны – равны 0, согласно метода узловых напряжений составим два уравнения для узлов 1 и 2, однако в ветви между узлами 1 и 3 стоит идеальный источник ЭДС без внутреннего сопротивления, следовательно потенциал в узле 1 φ1 = -Е=-1В. Тогда достаточно одного уравнения для узла 2 где (См) (См) (А)

Подставим численные значения и определим потенциал в узле 2:

(В)

Зная потенциалы всех узлов определим токи в ветвях: (А) направление тока не совпадает с выбранным (А) направление тока совпадает с выбранным (А) (А) направление тока не совпадает с выбранным (А) направление тока не совпадает с выбранным (А) направление тока совпадает с выбранным (А) направление тока не совпадает с выбранным

3. Проверим результат решения по 1-му правилу Кирхгофа для узлов.

Для узла 1: Для узла 2: Для узла 3: Для узла 4:

1-й закон Кирхгофа для всех узлов выполняется – решение правильное.

Метод контурных токов

Контурные токи – это условно независимые, одинаковые для всех ветвей каждого контура токи (рис.1 , указанные пунктиром II , III), которые совпадают по модулю с соответствующими токами внешних ветвей (например, ), токи смежных ветвей равняются их сумме (если, направления контурных токов совпадают) или разности (если направления противоположны). Например, .  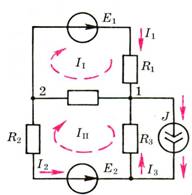 Рис.1. Введение контурных токов дает возможность исключить из системы по первому и второму законам Кирхгофа уравнения первого закона Кирхгофа, снизив размерность системы до m – (n – 1). Для схемы (рис.1) исключим I3 и I4 из двух первых уравнений системы: Из второго уравнения найдем I4, из первого – I3: Подставим полученную формулу в два последних уравнения системы Кирхгофа: Или относительно неизвестных I1 и I2: После введения обозначений (второе уравнение умножили на -1, чтобы III имел дополнительное значение) получим систему уравнений для контурных токов II и III: где R12 = R21 = R4 (взаимное сопротивление Rij будет иметь отрицательное значение, если II и III направлены навстречу друг другу); Е2 также отрицательна, поскольку направление Е2, противоположно по направлению току III, должно быть в левой части уравнения со знаком «-» но после перехода вправо получило знак «+». Обобщим систему для произвольного числа контуров: Элементы формируются согласно алгоритма метода контурных токов: 1. Выделить m – (n – 1) независимых контуров (каждый новый контур необходимо выбрать так, чтобы в него входил хотя бы один элемент электрической цепи, который не входит в другие контуры: например, для рис. 2, если выбраны контуры abd и bcd, то нельзя брать третьим контур abcd. 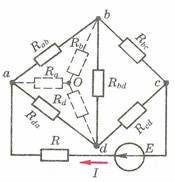  Рис.2. 2. Указать произвольно направления обхода контуров. Если на схеме уже обозначено направление токов в ветвях, то удобно направления контурных токов согласовать с направлением токов в ветвях. 3. Вычислить Rij: Rij равняется сумме сопротивлений всех элементов, входящих в i-й контур; Rij – равняется по модулю сумме сопротивлений ветвей, которые одновременно принадлежат i-му и j-му контурам; Rij больше нуля, если контурные токи i-го контура совпадают по направлению, и меньше нуля – при противоположных направлениях. 4. Вычислить правые части системы: Еi равняется алгебраической сумме ЭДС i-го контура; со знаком «+» берутся ЭДС, внутренняя стрелочка которых совпадает с направлением контурного тока i-го контура, «-» - если не совпадают. Если в семе есть источник тока J, то для его учета необходимо заблаговременно распределить ток J по ветвям любого незамкнутого контура, который дополняет ветвь с источником тока до замкнутого контура (в нашем случае – через R3, однако можно было бы и через R2 и R4). Полученное таким образом произведение J на соответствующее сопротивление необходимо перенести вправо, при этом необходимо поменять знак. 5. Решить систему уравнений относительно I. По контурным токам определить токи в ветвях. Во внешних ветвях они по модулю совпадают, во внутренних совпадающие по направлению складываются, направлены встречно – вычитаются. (В нашем примере I1 = I2; III = - I2; I1 – III = I4; ток I3 определим по первому закону Кирхгофа для узла 3: III – J + I3 = 0, откуда I3 = J - III).

Расчет электрических цепей методом наложения (суперпозиции) Ток в любой ветви сложной электрической цепи равняется алгебраической сумме отдельных токов от каждого источника электроэнергии. Этот принцип вытекает из свойства линейности уравнений электрической цепи относительно токов и ЭДС. Метод наложения состоит: в замене одной схемы с n источниками ЭДС и (или) тока n такими же схемами, с одним источником в каждой; расчет отдельных токов в ветвях цепи с одним источником и их алгебраическом сложении для определения токов заданной цепи с n источников. Например, вместо схемы (рис. 1, а) рассчитываются три схемы (рис. 1, б, в, г), а результаты алгебраически складываются:  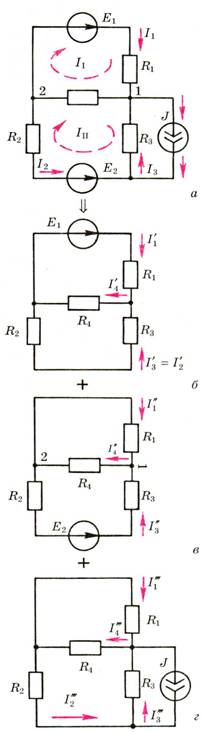 Рис. 1. При выключении источника ЭДС электрическая цепь закорачивается, поскольку ее Rвн = 0, а источники тока – разрывается, поскольку их Rвн → ∞.

Метод эквивалентного генератора В электрической цепи (рис. 1, а), изображенной в виде активного двухполюсника А с выделенным участком, имеющим сопротивление R, необходимо определить ток I. 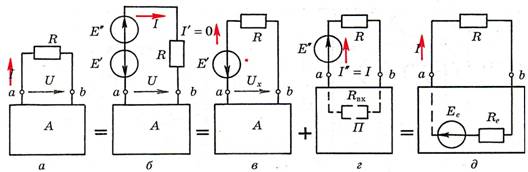  Рис. 1. Включим последовательно с R два источника ЭДС: Е' и Е'' (рис. 1, б), значения которых одинаковы и равняются напряжению между выводами a и bактивного двухполюсника при выключенном сопротивлении R, т.е. в режиме холостого хода: - Е' = Е'' = Uхх. Что бы ток I не изменился, Е' и Е'' направлены навстречу друг другу. По принципу наложения схема (рис. 1, б) представлена в виде двух схем, в одной из которых работает источник ЭДС Е' и все источники внутри активного двухполюсника (рис. 1, в), а во второй – (рис. 1, г) – только источник ЭДС Е''. По тому же самому принципу ток I равняется сумме токов I = I' + I''. Поскольку Е' = Е'' = Uxx , то во вспомогательной схеме (рис. 1, в) частичный ток I' по закону Ома равняется нулю: I' = (Uхх - Е')/R = 0. Таким образом, ток I'' (рис. 1, г) равняется искомому току I: где Rвх – входное или внутреннее сопротивление пассивного двухполюсника относительно выводов a и b (рис. 1, г). Такой же ток будет и в эквивалентной схеме (рис. 1, д), если Ее = Uхх и Re = Rвх. Ток I для сопротивления в заданной схеме (рис. 1, а) и в схеме (рис. 1, д) одинаков, следовательно, активный двухполюсник можно заменить эквивалентным генератором. Метод эквивалентного генератора целесообразно применять, если необходимо найти ток в одной ветви сложной электрической цепи, без расчета других токов. Для расчета тока в сопротивлении R сначала отключают это сопротивление и определяют напряжение Uхх на его выводах. Далее необходимо исключить все ЭДС в оставшейся схеме (внутренние сопротивления источников остаются) и определить сопротивление относительно выводов исключенного сопротивления. Затем, по указанной выше формуле, определяют ток. Пример. Схема (рис.2) относительно сопротивления R2 может быть представлена эквивалентным генератором с параметрами Rн = Rвх = R1R3/(R1 + R3) и ЭДС Ее = Uхх = ER3/(R1 + R2), которые определяются в режиме холостого хода. 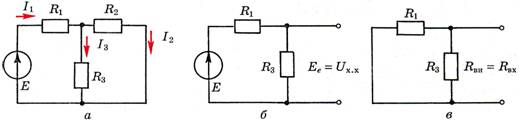Тогда   Рис. 2.