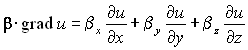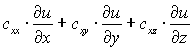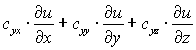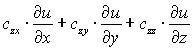27 Понятие о системе комсоль…

COMSOL Multiphysics - это мощная интерактивная среда для моделирования и расчетов большинства научных и инженерных задач основанных на дифференциальных уравнениях в частных производных (PDE) методом конечных элементов.

С этим программным пакетом мы можем расширять стандартные модели, использующие одно дифференциальное уравнение (прикладной режим) в мультифизические модели для расчета связанных между собой физических явлений. Расчет не требует глубокого знания математической физики и метода конечных элементов. Это возможно благодаря встроенным физическим режимам, где коэффициенты PDE задаются в виде понятных физических свойств и условий, таких как: теплопроводность, теплоемкость, коэффициент теплоотдачи, объемная мощность и т.п. в зависимости от выбранного физического раздела. Преобразование этих параметров в коэффициенты математических уравнений происходит автоматически. Взаимодействие с программой возможно стандартным способом – через графический интерфейс пользователя (GUI), либо программированием с помощью скриптов на языке COMSOL Script или языке MATLAB. Для решения PDE, COMSOL Multiphysics использует метод конечных элементов (FEM). Программное обеспечение запускает конечноэлементный анализ вместе с сеткой, учитывающей геометрическую конфигурацию тел, и контролем ошибок с использованием разнообразных численных решателей. Так как многие физические законы выражаются в форме PDE, становится возможным моделировать широкий спектр научных и инженерных явлений из многих областей физики таких как: акустика, химические реакции, диффузия, электромагнетизм, гидродинамика, фильтрование, тепломассоперенос, оптика, квантовая механика, полупроводниковые устройства, сопромат и многих других.

Кроме вышеперечисленного, программа позволяет с помощью переменных связи (coupling variables) соединять модели в разных геометриях и связывать между собой модели разных размерностей.

28 Классификация дифуров…

Программа основана на системе дифференциальных уравнений в частных производных. Существует три математических способа задания таких систем:

• Коэффициентная форма, предназначенная для линейных и близких к линейным моделей

• Генеральная форма, для нелинейных моделей

• Слабая форма (Weak form), для моделей с PDE на границах, ребрах или для моделей, использующих условия со смешанными и производными по времени.

Используя эти способы, можно изменять типы анализа, включая:

• Стационарный и переходный анализ

• Линейный и нелинейный анализ

• Модальный анализ и анализ собственных частот

29Коэффициентная форма представления краевой задачи

Сначала эту форму рассмотрим для скалярного поля. Пусть в одномерном, двумерном или трёхмерном пространстве имеется некоторая область , в которой нужно рассчитать скалярное поле. Обозначим границу этой области . Система FEMLAB позволяет моделировать скалярные поля, описываемые уравнениями вида: 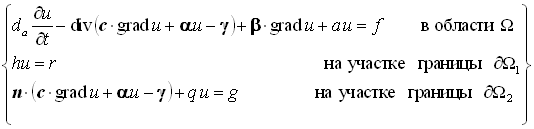, (1) где u – искомое скалярное поле; d_a, a, f – заданные скалярные поля; , , – заданные векторные поля; c – заданное скалярное или тензорное (второй валентности) поле. Поля d_a, c, , , , a, f называют коэффициентами PDE. Иначе их называют параметрами материальных свойств среды. Скалярные переменные h, r, q, g называют коэффициентами граничных условий.

Система уравнений (1) называется коэффициентной формой представления краевой задачи (Coefficient form). Если d_a=0, то краевая задача называется стационарной (Stationary), иначе – нестационарной (Time dependent). Если первую производную по времени заменить на вторую, то (1) будет называться волновым расширением нестационарной краевой задачи (Wave extension). Второе уравнение (1) называется граничным условием первого рода (граничным условием Дирихле). Третье уравнение (1) называется граничным условием второго рода (граничным условием Неймана). Если коэффициенты PDE и граничных условий не зависят от искомого поля u и его дифференциальных операторов, то краевая задача называется линейной, в противном случае – нелинейной. Коэффициентная форма пригодна для решения линейных и несущественно-нелинейных краевых задач.

Искомое скалярное поле u в терминологии FEMLAB называется зависимой переменной. Пространственные координаты x, y, z называются независимыми переменными. Есть ещё одна особая независимая переменная для нестационарных задач – это время t. Все эти имена переменных могут записываться в выражениях FEMLAB. В этих выражениях могут встречаться также и другие переменные. Перечень их сведём в таблицу.

Области	Размерность PDE
	1D	2D	3D
Точка		u	u
Ребро			u
Граница	alux, au, beu, cux, f, g, gax, nalu, ncu, nga, qu, u, ux	alux, aluy, au, beu, cux, cuy, f, g, gax, gay, nalu, ncu, nga, qu, u, ux, uy	alux, aluy, aluz, au, beu, cux, cuy, cuz, f, g, gax, gay, gaz, nalu, ncu, nga, qu, u, ux, uy, uz
Зона	abscu1x, absux, alux, au, beu, cux, dau, f, gax, u, ux, uxx	abscu1x, absux, alux, aluy, au, beu, cux, cuy, dau, f, gax, gay, u, ux, uy, uxx, uxy, uyx, uyy	abscu1x, absux, alux, aluy, aluz, au, beu, cux, cuy, cuz, dau, f, gax, gay, gaz, u, ux, uy, uz, uxx, uxy, uxz, uyx, uyy, uyz, uzx, uzy, uzz

Интерпретацию перечисленных переменных сведём в следующую таблицу.

Имя переменной в системе FEMLAB	Определяющее математическое выражение
abscu1x
absux
alux, aluy, aluz
au
beu
cux
cuy
cuz
dau	da u
f	f
g	g
gax, gay, gaz
nalu
ncu
nga
qu	q u
u	u
ux, uy, uz
uxx, uxy, uxz, uyx, uyy, uyz, uzx, uzy, uzz

В трёхмерном режиме тензорный коэффициент c имеет 9 компонентов. В строке редактирования c компоненты этого тензора записываются через пробелы в столбцовом порядке: c_xx c_yx c_zx c_xy c_yy c_zy c_xz c_yz c_zz . Если тензор c симметричный, то можно в строку редактирования вписывать только его верхнюю треугольную часть: c_xx c_xy c_yy c_xz c_yz c_zz . Если тензор c ортотропный (диагональный), то можно вписывать только его диагональные компоненты: c_xx c_yy c_zz . Если коэффициент c скалярный (шаровой тензор), то можно вписывать только один компонент c.