Моп_Л9_2сПМ

Моп_Л9_2сПМ.doc из файла МЕТОД АППРОКСИМИРУЮЩЕГО ПРОГРАММИРОВАНИЯ.doc из IASA_6-3.mht и IASA_6-4.mht

Лекция 9 –ПМ, 5-ИНФ

МЕТОДЫ АППРОКСИМИРУЮЩЕГО ПРОГРАММИРОВАНИЯ

Метод аппроксимирующего программирования (МАП) основан на линеаризации исходной задачи НП и замене ее последовательностью промежуточных задач ЛП. Его называют также градиентным методом с малой длиной шага в отличие от обычных градиентных методов .

Итак, пусть задача НП задана в виде:

минимизировать (1)

при условиях (2)

(3)

После линеаризации в окрестности точки задача формулируется следующим образом:

Минимизировать (4)

при условии, что имеют место ограничения в виде равенств

(5)

и неравенств (6)

где (7)

Пусть - допустимая точка в . Произведем замену в (2), (3) нелинейных функций их аппроксимациями в окрестности точки . В результате получим соотношения (5), (6). Далее решаем задачу ЛП, представляемую этими соотношениями при следующем добавочном условии:

(8)

где - абсолютное приращение , а - маленькая величина, ограничивающая длину шага при перемещении в произвольном направлении и не позволяющая выходить вектору за пределы допустимой области задачи (4).

Решение задачи (4) с учетом (5), (6) для разности дает . Вычислив , повторяем выше указанную процедуру при постепенном уменьшении , чтобы довести отклонение элементов до величины, определяемой принятым допуском, и стремимся достичь такой ситуации, когда минимизирующая поправка к найденному на предыдущей итерации значению оказывается меньше некоторого наперед заданного числа.

В задаче (4) дополнительные ограничения для можно ввести и другим способом. Обозначим при через , а при через . Тогда прежде чем реализовать очередную аппроксимирующую процедуру, необходимо учесть ограничения для допустимых перемещений в пространстве решений, которые задаются следующими соотношениями:

,

где (9)

(10)

- максимальное допустимое перемещение вдоль -й оси координат на -м шаге; - нижняя и верхняя границы для переменной . Если , то . Когда значение близко к своему верхнему пределу, т.е. , то

(11)

и, следовательно, (12)

или , что гарантирует не превышение переменной своего верхнего предела. Аналогичные рассуждения для случая, когда , показывают, что в этом случае . Соотношения (5), (6), (12) образуют систему линейных неравенств и уравнений, которые подлежат решению методами линейного программирования. Для этого решения можно использовать симплекс-метод, но сначала необходимо привести все ограничения к каноническому виду, введя свободные переменные, а затем и искусственные. Пока на каждом шаге (итерации) полученные решения являются допустимыми, МАП работает весьма быстро. Однако в случае, когда на каком-то шаге вектор выходит за пределы допустимой области, процесс поиска в значительной мере замедляется. В процессе решения задач ЛП вначале стремятся удовлетворить ограничениям, которые не позволяют вектору выходить за пределы допустимой области, а затем пытаются улучшить значения целевой функции, и именно этим МАП отличается от других методов.

Отметим следующие трудности, которые возникают при решении задач НП методом МАП .

1. Оптимизация происходит очень медленно, если стремиться сделать векторы , и допустимыми или очень близкими к допустимым. На рис. 6.10 представлен случай, когда малый допуск при учете ограничений приводит к тому, что поиск оптимального решения оказывается слишком мелко-шаговым и протекает медленно.

При увеличении допуска решение задачи НП может остаться недопустимым, или возникает потребность остановки ЭВМ из-за ограничения ресурса машинного времени.

2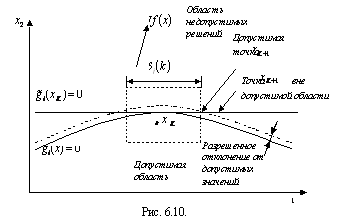. Трудно сравнивать между собой следующие один за другим два вектора та , которые приводят к различным значениям и в различной степени нарушают множество ограничений.

Например, необходимо сравнить векторы и . Пусть , но ограничение для нарушается сильнее, чем для . Ответить на вопрос, какой из векторов , будет предпочтительнее, дать весьма трудно.

3. Если целевая функция характеризуется высокой степенью нелинейности, то направление поиска оптимальной точки, получаемое путем решения линеаризованной задачи, может быть вычислено слишком неточно.

4. При использовании метода МАП трудно придумать такую процедуру учета исходных данных, которая ускоряла бы процесс оптимизации.

Характеристика методов поиска экстремума нелинейных функций при ограничениях

Решение задач нелинейной оптимизации при ограничениях (т.е. задач НП) вызывает значительно большие трудности, чем без ограничений (т.е. задач безусловной оптимизации) в силу наличия ограничивающих условий. Известные различные вычислительные процедуры для задач НП с ограничениями опираются на один из следующих подходов.

Распространение аппарата линейного программирования на нелинейные условия путем многократной используемой процедуры линейной аппроксимации (методы аппроксимирующего программирования).

Преобразование задачи НП с ограничениями в эквивалентную ей последовательность задач безусловной оптимизации путем введения в рассмотрение штрафных функций (методы штрафных функций).

Использование скользящих допусков, позволяющих оперировать в процессе решения задачи, как с допустимыми, так и с недопустимыми векторами в пространстве решений. Основные характеристики и потенци-альные возможности ряда методов решения задач НП приведены в табл.1

Таблица 1 Условные обозначения:

¹ - метод не эффективен при решении задач с нелинейными ограничениями;

² - применяется только для задач с линейными ограничениями;

Л - линейные методы; НЛ - нелинейные методы;

Д - допустимые; НД - недопустимые.

№ Структурные Характеристики	Методы поиска - прямые						Методы штрафных функций
	Метод апрокси­мирующего программи-рования	Метод Розена	Обобщен-ный градиент-ный метод	Проекцион-ный вариант метода Д-Ф-П	Метод допусти-мых направле-ний	Метод приведен-ного градиента	Метод Розен-брока	Метод баръер-ных поверхностей	Метод Фиакко-Мак-Кормика
1. Целевая функция	Л и НЛ	Л и НЛ	Л и НЛ	Л и НЛ	Л и НЛ	Л и НЛ	Ли НЛ	Л и НЛ	Л и НЛ
2.Позволяет рабо-тать с ограниче-ниями типа =	Нет	Л2	Л и НЛ	Л	Нет	Л и НЛ	Нет	Нет	Л
3. Позволяет работать с ограни-чениями типа ≤	НЛ1	Л и НЛ1	Л и НЛ	Л и НЛ	Л и НЛ	Л и НЛ	Л и НЛ	Л и НЛ	Л и НЛ
4.Начальная точка	Д	Д	Д и НД	Д	Д	Д и НД	Внутренняя	Внутрен-няя	Внутренняя
5. Позволяет ре-шать невыпуклые задачи	Да	Да	Да	Да	Да	Да	Да	Да	Да
6. Скорость сходимости	Низкая	Высо-кая	Низкая	Средняя	Высокая	Средняя	Средняя	Средняя	Высокая
7. Промежуточные точки	Д	Д	Д и НД	Д	Д	Д	Д	Д	Д

3