
Методы возможных направлений
Этот класс методов решения задач НП основан на движении из одной допустимой точки к другой с лучшим значением целевой функции.
Типичная
стратегия поиска в алгоритмах этого
класса состоит в следующем. Возьмем
текущую допустимую точку
![]() и
найдем направление Sk такое,
что при достаточно малых k выполняются
следующие два условия: 1) точка
и
найдем направление Sk такое,
что при достаточно малых k выполняются
следующие два условия: 1) точка
![]() является
допустимой; 2)
является
допустимой; 2)
![]()
После
нахождения допустимого направления
![]() решается
задача одномерной минимизации по
параметру
решается
задача одномерной минимизации по
параметру
![]() для
нахождения оптимальной длины шага в
направлении Sk.
Далее перемещаемся в точку
для
нахождения оптимальной длины шага в
направлении Sk.
Далее перемещаемся в точку
![]() и
процесс поиска повторяется.
и
процесс поиска повторяется.
Метод Зойтендейка
Типичным представителем класса методов возможных направлений является метод Зойтендейка. На каждой итерации метода находят возможное направление спуска, а затем проводят оптимизацию вдоль этого направления. Для изложения идеи метода введем ряд необходимых понятий.
Напомним
Определение
2.
Рассмотрим задачу минимизации
![]() при
условии, что xD
Rn,
где D-
непустое множество. Ненулевой
S называется
возможным направлением спуска в точке
xD,
если существует
такое
при
условии, что xD
Rn,
где D-
непустое множество. Ненулевой
S называется
возможным направлением спуска в точке
xD,
если существует
такое
![]() ,
что
,
что
![]() и
x+SD для
всех
и
x+SD для
всех
![]() .
.
Вначале рассмотрим случай, когда ограничения линейные и задача НП имеет вид:
Минимизировать
![]() (10)
(10)
при
условиях
![]() (11)
(11)
![]() (12)
(12)
где
![]() -
матрица порядка
-
матрица порядка
![]() ;
;
![]() -
матрица порядка
-
матрица порядка
![]() ;
b –
m-мерный
вектор; k –
l-мерный
вектор.
;
b –
m-мерный
вектор; k –
l-мерный
вектор.
Справедливо следующее утверждение.
Лемма
2. Рассмотрим
задачу минимизации
(10)-(12). Пусть
x -
допустимая
точка и предположим, что
![]() ,
где
,
где
![]() ,
а
,
а
![]() .
.
Ненулевой
вектор S является
возможным направлением в точке
![]() в
том и только в том случае, если
в
том и только в том случае, если
![]() и
и
![]() .
Если, кроме
того, f(x)T·S<0,
то
S является
возможным
направлением спуска.
.
Если, кроме
того, f(x)T·S<0,
то
S является
возможным
направлением спуска.
Доказательство этого утверждения очень простое. Предлагаем читателю выполнить это самостоятельно.
Проиллюстрируем геометрически множество возможных направлений спуска на следующем примере.
Пример
1. Минимизировать
![]() при
условиях
при
условиях
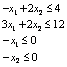
Выберем
![]() и
заметим, что первые два ограничения
являются активными в этой точке. В
частности, матрица
и
заметим, что первые два ограничения
являются активными в этой точке. В
частности, матрица
![]() из
вышеприведенной леммы 2, равна
из
вышеприведенной леммы 2, равна
![]() .
Следовательно, вектор S является
возможным направлением тогда и только
тогда, когда
.
Следовательно, вектор S является
возможным направлением тогда и только
тогда, когда
![]() т.е.
в том случае, если
т.е.
в том случае, если
![]()
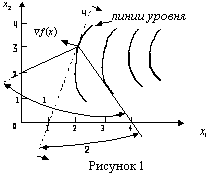
На рис. 1. изображена совокупность этих направлений, образующая конус возможных направлений. Здесь 1 - конус возможных направлений; 2 - конус возможных направлений спуска; 3 - линии уровня целевой функции; 4 - полупространство направлений спуска.
Если
вектор S удовлетворяет
неравенству
![]() ,
то он является направлением спуска.
Таким образом, совокупность возможных
направлений спуска определяется открытым
полупространством
,
то он является направлением спуска.
Таким образом, совокупность возможных
направлений спуска определяется открытым
полупространством
![]() .
Пересечение конуса возможных направлений
с этим полупространством задает множество
всех возможных направлений спуска.
.
Пересечение конуса возможных направлений
с этим полупространством задает множество
всех возможных направлений спуска.
Построение возможных направлений спуска
Пусть
задана текущая допустимая точка
x.
Как показано в лемме 2, ненулевой вектор
![]() будет
возможным направлением спуска, если
будет
возможным направлением спуска, если
![]() .
Естественный подход к построению такого
направления заключается в минимизации
линейной по S
функции
.
Естественный подход к построению такого
направления заключается в минимизации
линейной по S
функции
![]() при
условиях:
при
условиях:
![]() .
Однако, если существует такой вектор
S*,
что
.
Однако, если существует такой вектор
S*,
что
![]() ,
и выполняются условия а) и б), то оптимальное
значение целевой функции сформулированной
задачи равно -
,
и выполняются условия а) и б), то оптимальное
значение целевой функции сформулированной
задачи равно -![]() ,
так как ограничениям этой задачи
удовлетворяет любой вектор S*,
где -
любое большое число.
,
так как ограничениям этой задачи
удовлетворяет любой вектор S*,
где -
любое большое число.
Следовательно, в задачу должно быть включено условие, которое бы ограничивало вектор S,. Такое ограничение называют нормирующим. Возможны различные формы нормирующего ограничения. Ниже приведены три задачи отыскания (наилучшего) направления спуска, в каждой из которых используются различные условия нормировки.
Задача
P1:
минимизировать
![]()
при условиях
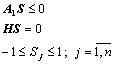
Задача
P2:
минимизировать
![]() при условиях:
при условиях:
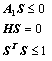
Задача
P3:
минимизировать
![]() при условиях:
при условиях:
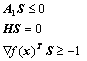
Задачи P1 и P3 являются задачами ЛП и, следовательно, их можно решить симплекс-методом.
Так как S=0 является допустимой точкой в каждой из приведенных выше задач, а значение целевой функции в этой точке равно 0, то ее оптимальное значение в задачах P1, P2, P3 не может быть положительным. Если минимальное значение целевой функции в задачах, P1, P2, P3 отрицательно, то по лемме 2 нами построено возможное направление спуска. С другой стороны, если минимальное значение целевой функции равно нулю, то, как будет показано ниже, точка x является точкой Куна-Таккера.
Лемма
3. Рассмотрим
задачу минимизации
![]() при
условиях
при
условиях
![]() .
Пусть
x -
допустимая
точка, в которой
.
Пусть
x -
допустимая
точка, в которой
![]() ,
где
,
где
![]() .
Вектор
x является
точкой Куна-Таккера тогда и только
тогда, когда оптимальное значение
целевой функции в задачах,
P1,
P2,
P3 равно
нулю.
.
Вектор
x является
точкой Куна-Таккера тогда и только
тогда, когда оптимальное значение
целевой функции в задачах,
P1,
P2,
P3 равно
нулю.
Доказательство.
Как следует из теоремы Куна-Таккера,
x будет
точкой Куна-Таккера тогда и только
тогда, когда существуют векторы
![]() такие,
что
такие,
что
![]() .
(13)
.
(13)
Согласно
следствию из леммы Фаркаша система (13)
разрешима тогда и только тогда, когда
система неравенств
![]() не
имеет решений, т.е. когда оптимальное
значение целевой функции в задачах,
P1,
P2,
P3 равно
нулю.
не
имеет решений, т.е. когда оптимальное
значение целевой функции в задачах,
P1,
P2,
P3 равно
нулю.
Итак, мы показали, как найти возможное направление спуска.
Пусть
теперь
![]() -
текущая точка;
-
текущая точка;
![]() -
возможное направление спуска. В качестве
следующей точки
-
возможное направление спуска. В качестве
следующей точки
![]() выбирается
выбирается
![]() ,
где длина шага
,
где длина шага
![]() определяется
из решения следующей задачи одномерной
оптимизации:
определяется
из решения следующей задачи одномерной
оптимизации:
Минимизировать
![]() по
по
![]() (14)
(14)
при
условиях ![]() ,
(15)
,
(15)
![]() .
(16)
.
(16)
Предположим,
что
![]() .
Тогда задачу (14)-(16) можно упростить
следующим образом. Заметим, что
.
Тогда задачу (14)-(16) можно упростить
следующим образом. Заметим, что
![]() .
Значит, ограничение (16) излишне. Так как
.
Значит, ограничение (16) излишне. Так как
![]() ,
то
,
то
![]() для
всех
для
всех
![]() .
Итак, остается только одно ограничение
.
Итак, остается только одно ограничение
![]() ,
и задача оптимизации (14)-(16) приводится
к следующей задаче одномерной оптимизации:
,
и задача оптимизации (14)-(16) приводится
к следующей задаче одномерной оптимизации:
минимизировать
![]() по
по
![]() (17)
(17)
где ![]() ,
(18)
,
(18)
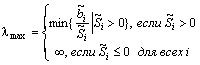 (19)
(19)
![]() .
(20)
.
(20)
