Файл Моп_Л8_2сПМ.doc из "Прямые методы условной оптимизации-Лекц1.doc" из А.Г.Трифонов. "Постановка задачи оптимизации и численные методы ее решения" 3. Методы условной оптимизации. I:\RES_H\WORK\EDUCATION\ХНУРЭ - учебные курсы\МЕТОДЫ ОПТИМИЗАЦИИ\MO\MO\NewLab20807\Doc\MProection\Метод проекций гр.doc , "методы возм_направ Л1.doc"

Прямые методы условной оптимизации Лекция 1

В общем случае численные методы решения задач нелинейного программирования можно разделить на прямые и непрямые. Прямые методы оперируют непосредственно с исходными задачами оптимизации и генерируют последовательности точек {x[k]}, таких, что f(х[k+1]) < f(x[k]). Здесь в [] – индекс. В силу этого такие методы часто называют методами спуска.

Математически переход на некотором k-м шаге (k. 0, 1, 2, ...) от точки х[k] к точке x[k+1] можно записать в следующем виде:

x[k+l] x[k] + a_kp[k],

где р[k] — вектор, определяющий направление спуска;

а_k — длина шага вдоль данного направления.

При этом в одних алгоритмах прямых методов точки х[k] выбираются так, чтобы для них выполнялись все ограничения задачи, в других эти ограничения могут нарушаться на некоторых или всех итерациях. Таким образом, в прямых методах при выборе направления спуска ограничения, определяющие допустимую область G, учитываются в явном виде.

Непрямые методы сводят исходную задачу нелинейного программирования к последовательности задач безусловной оптимизации некоторых вспомогательных функций. При этих методах ограничения исходной задачи учитываются в неявном виде. К ним относятся методы функции Лагранжа и штрафных функций, рассмотренные на прошлых лекциях. Рассмотрим теперь некоторые алгоритмы прямых методов.

Метод проекции градиента

Проведем сначала «правдоподобные рассуждения» и рассмотрим алгоритм данного метода применительно к задаче оптимизации с ограничениями-неравенствами. В качестве начальной выбирается некоторая точка допустимой области G. Если х[0] - внутренняя точка множества G

(Рис. 1), то рассматриваемый метод является обычным градиентным методом:

x[k+l] x[k] –a_kf’(x[k]), k 0, 1, 2, ...,

где градиент целевой функции f(х) в точке x[k].

После выхода на границу области G в некоторой граничной точке х[k] , k 0, 1, 2,..., движение в направлении антиградиента -f’(х[k]) может вывести за пределы допустимого множества (см. Рисунок 1). Поэтому антиградиент проецируется на линейное многообразие М, аппроксимирующее участок границы в окрестности точки х[k]. Двигаясь в направлении проекции вектора -f'(x[k]) на многообразие М, отыскивают новую точку х[k+1], в которой f(х[k+1]) f(x[k]), принимают х[k+1] за исходное приближение и продолжают процесс. Проведем более подробный анализ данной процедуры.

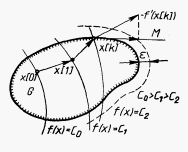
Рисунок 1. Геометрическая интерпретация метода проекции градиента

В точке х[k] часть ограничений-неравенств удовлетворяется как равенство:

h_j(x) 0, j 1, ..., l; l < m. Такие ограничения называют активными.

Обозначим через J набор индексов j (1 j l) этих ограничений. Их уравнения соответствуют гиперповерхностям, образующим границу области G в окрестности точки х[k] . В общем случае эта граница является нелинейной (см. рис.1). Ограничения h_j(x), j J, аппроксимируются гиперплоскостями, касательными к ним в точке х[k]:

Полученные гиперплоскости ограничивают некоторый многогранник М, аппроксимирующий допустимую область G в окрестности точки х[k] (см. Рис. 1).

Проекция р[k] антиградиента -f'(x[k]) на многогранник вычисляется по формуле p[k]  [-f’(x[k])].

Здесь  - оператор ортогонального проектирования, определяемый выражением  E – A^T(AA^T)^-1A, где Е - единичная матрица размерности пп;

А - матрица размеров l  n . Она образуется строками – транспонирован­ными вектор-столбцами градиентов активных ограничений из множества J: а_j=(h_j)^T, j 1, ..., l.

(см. Лекцию 4 о конусах и проекциях – файл Моп_Л4_2сПМ.doc. Здесь x[k]Г(G) является началом координат, из которого проводится радиус-вектор f. Значит b=0, и это – проекция на подпространство, а не на многообразие ).

Далее осуществляется спуск в выбранном направлении: x[k+1] x[k] + _kp[k]. Можно показать, что точка х[k+1] является решением задачи минимизации функции f(х) в области G тогда и только тогда, когда [-f’(x[k])] 0, т. е, и u (u₁, ..., u_l) (A^TA)^-1A^T(-f (х[k])) > 0.

Эти условия означают, что антиградиент (-f (х[k])) целевой функции является линейной комбинацией с неотрицательными коэффициентами градиентов активных ограничений h_j(x) 0. Напомним, что h есть нормаль касательной гиперплоскости.

В соответствии с изложенным, алгоритм метода проекции градиента состоит из следующих операций.

1. В точке х[k] определяется направление спуска р[k].

2. Находится величина шага _k.

3. Определяется новое приближение х[k+1].

Рассмотрим детально каждую из этих операций.

1. Определение направления спуска состоит в следующем. Пусть найдена некоторая точка х[k] G и известен набор активных ограничений h_i(х[k]) 0, j J. На основании данной информации вычисляют (-f (х[k])) и определяют проекцию  [-f (х[k])]. При этом возможны два случая:

а)  [-f’(х[k])] не равна 0. В качестве направления спуска р[k] принимают полученную проекцию;

б)  [-f (х[k])] 0, т. е.

Данное выражение представляет собой систему из п уравнений для определения коэффициентов и_j. Если все и_j 0, j J, то в соответствии с вышеизложенным точка х[k] является решением задачи. Если же некоторый компонент и_q 0, то соответствующий ему градиент выводится из матрицы А и порождается новая проецирующая матрица . Она определит новое направление спуска.

2. Для определения величины шага _k целевая функция минимизируется по направлению р[k] при условии соблюдения ограничений задачи с установленной точностью. Последняя задается введением некоторого положительного числа . Считают, что точка х удовлетворяет условиям задачи с заданной точностью, если h_i(х) , j 1, ..., m. Величина шага _k определяется решением задачи вида:

f(x[k] + р[k])  min;

h_j(x[k] + р[k]) , j 1, ..., m.

3. Определение нового приближения состоит в том, что очередная точка вычисляется по формуле

x[k+1] x[k] + _k р[k].

Признаком сходимости является стремление к нулю векторов р[k].

Рассмотренный метод является в некотором смысле аналогом градиентных методов для решения задач на безусловный экстремум, и ему свойствен их недостаток - медленная сходимость.

Приведем несколько утверждений, обосновывающих метод и оценивающих скорость его сходимости (изложение согласно книге: Сухарев и др. – Курс методов оптимизации)

Рассмотрим элементы теории метода проекции градиента для решения задачи следующего вида: (1)

где  - замкнутое выпуклое множество в , дифференцируемая функция на . Пусть является оптимальным решением задачи (1).

Напомним вначале свойства проекции точки на множество.

Проекцией точки на множество называется точка такая, что , т.е. точка, ближайшая к a среди всех точек из X. Если , то , если X замкнуто. Если же a не принадлежит X, и X - открыто, то проекция не существует.

Из определения следует, что является решением следующей задачи оптимизации: . (2)

Лемма 1 Пусть замкнутое выпуклое множество в . Тогда

1. Проекция любой точки существует и единственна;

2. Точка является проекцией точки a на множество X в том и только в том случае, если (3)

3. Для всех точек справедливо неравенство

(4)

т.е. оператор проектирования обладает свойством нерастяжения расстояний.

Доказательство леммы приведено в [Сухарев, с. 225].

Сформулируем необходимое и достаточное условие оптимальности для выпуклой задачи.

Лемма 2. Пусть множество X выпукло и замкнуто, функция f выпукла на X и дифференцируема в точке . Тогда является решением задачи (1) в том и только в том случае, если

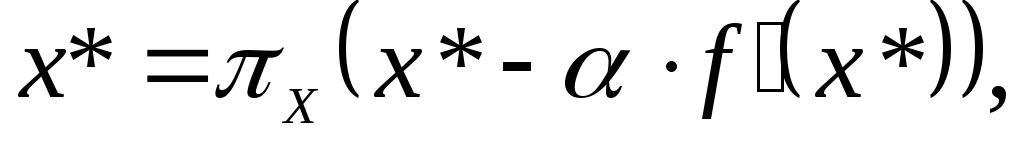(5)

при произвольном .

Доказательство леммы приведено в [Сухарев, с. 226].

Теперь рассмотрим алгоритм метода проекции градиента и его сходимость. В методе проекции градиента в качестве очередной точки приближения к решению задачи (1) выбирается проекция точки на множество X той точки, которая получается по градиентному методу:

, где (6)

Коэффициенты можно выбирать различными способами. (см. например, книги: Сухарев и др. или Реклейтис и др.). Рассмотрим теорему о сходимости проекции градиента с априорным выбором коэффициентов , то есть последовательность выбирают заранее, до начала вычислений (например, , где k=0,1,2,...).

Теорема 1. Пусть множество X выпукло и замкнуто, функция f сильно выпукла с константой и дифференцируема на X, причем ее градиент удовлетворяет условию Липшица:

(7)

Тогда последовательность , генерируемая по формуле (6), где произвольная точка из X, а сходится к решению задачи (1) со скоростью геометрической прогрессии:

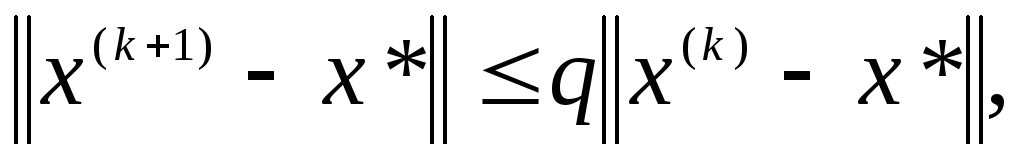(8)

где

Доказательство теоремы приведено в [Сухарев, с. 226].

Замечания:

1. В рассмотренном методе на каждой k-ой итерации требуется производить операцию проектирования точки на множество X, то есть решать задачу вида (2) при 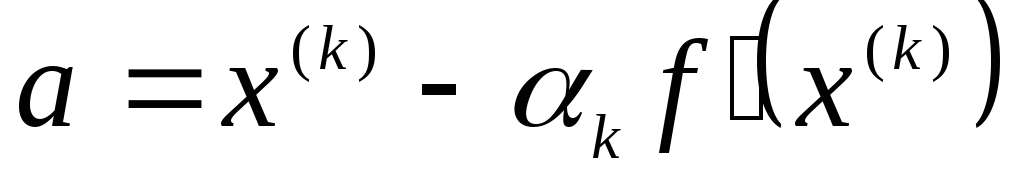. В некоторых случаях удается указать явный вид проекции, например, если множество X  шар, координатный параллелепипед, полупространство, гиперплоскость, аффинное множество. Однако, если X задается с помощью более или менее сложной системы равенств и неравенств, то метод проекции градиента практически неприменим, так как задача (2) оказывается не проще исходной.

2. В большинстве практических задач константы 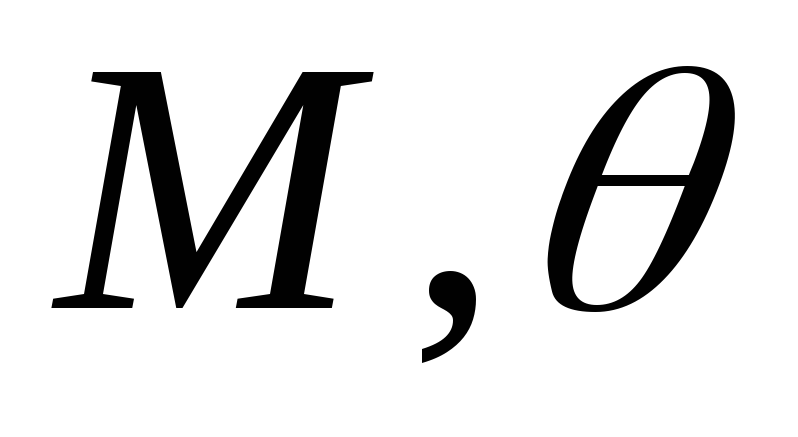из теоремы 1 обычно неизвестны, что затрудняет отыскание . Тогда можно использовать другие правила выбора длины шага, например, различные модификации метода наискорейшего спуска с приближенным решением задач одномерной минимизации по или правило дробления шага [Реклейтис и др.].

3. Используя идею проектирования, можно модифицировать применительно к задачам условной оптимизации и другие методы безусловной оптимизации, в том числе метод Ньютона и метод сопряженных направлений.

Пример: Решить методом проекции градиента:

(9)

. (10)

Решение. Задачу (9)-(10) решим методом проекции градиента, используя соотношение (6). Выберем начальное приближение . Пусть шаг в выражении (6) равен . Критерий останова выберем следующий: , где .

Итерация 1. В соответствии с выражением (6) определяем .

, .

Точка выходит за пределы области X. Так как множество X- координатный параллелепипед, то можно указать явный вид проекции точки на множество. Известно, что если – координатный параллелепипед, то : 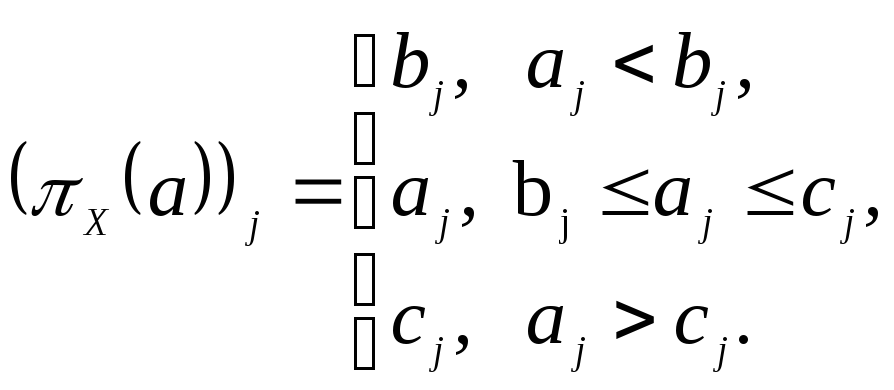(см.[Сухарев, с.227], а также лекцию о проекциях.

В нашем случае , .

Так как , то проверяем критерий останова: . Критерий останова не выполняется, значит, переходим к следующей итерации.

Итерация 2. В соответствии с выражением (6) определяем

.

, .

Точка выходит за пределы области X.

Значит, , . .

Критерий останова выполняется, значит, процесс вычислений закончен.

Вспомним некоторые определения и теоремы из прошлых лекций по математическому программированию.

Система из m линейных неравенств (ЛН) Ax  b (1)

называется разрешимой, если  x≥0: Ax  b, xRⁿ, bR^m и неразрешимой - в противном случае.

ОзЛП max c, x Ax  b (2)

разрешима, когда разрешима система (1) и максимум в (2) достигается.

Определение 1. Линейное неравенство c, x  d (3)

является следствием разрешимой системы линейных неравенств (1), если для любого x, удовлетворяющего (1), выполнено (3).

Пусть - вектор-строка матрицы А, т.е. коэффициенты i-го неравенства из (1); .

Лемма 1 (Фаркаша о неразрешимости).  Система ЛН (1) неразрешима тогда и только тогда, когда разрешима система

Теорема 1. (Куна-Таккера) будет использована в следующей форме

Пусть функции , имеют непрерывные частные производные на некотором открытом множестве Rⁿ, содержащем точку x*. Если x* является точкой минимума функции  при ограничениях , удовлетворяющих  условию регулярности в виде линейной независимости векторов , то существуют такие неотрицательные множители Лагранжа  , что

                             (4)

                 (5)

Определим функцию Лагранжа как обычно:

                           (6)

Тогда теорему Куна-Таккера можно записать в виде

= (__{}_m)^T, _i≥0,

                                 (7)

                              (8)

               (9)

Заметим, что множители Лагранжа _i в задаче НП с ограничениями-равенствами являются знако-неопределенными, тогда как в теореме Куна-Таккера они должны быть неотрицательными.