Моп_Л5_2сПМ.doc из 8_Опорные_векторы.rtf, 6_Экстремальные_свойства_ВФ_сент_9_2008.rtf, 5_Конусы_РВН_сент_9_2008.rtf

Лекция 5

Тема 5. Конусы релаксационных и возможных направлений.

Определение 1.Пусть функция определена на. Векторназываетсярелаксационным направлением (направлением убывания) функции в точке, если существует числотакое, что для любоговыполняется неравенство.

Обозначим множество релаксационных направлений функции в точке через .

Теорема 1. Пусть функция выпукла на. Тогда для любого множество– выпуклый конус.

Доказательство. Пусть вектор ,число .Тогда согласно определению 1 имеем

для любого 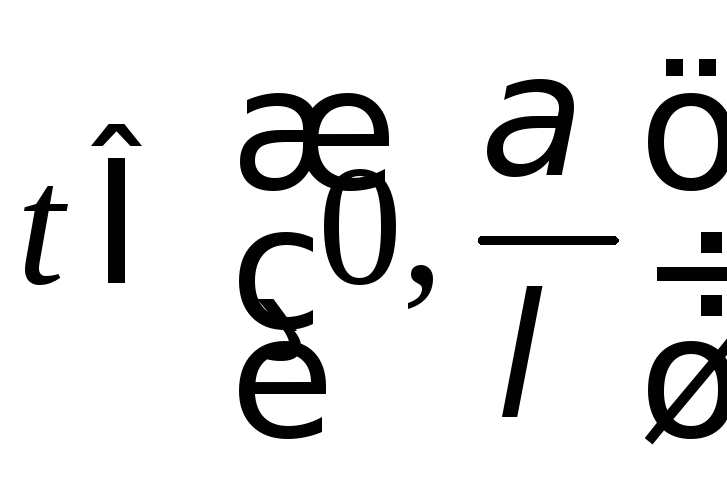,то есть вектор .

Проверим теперь выполнение второго требования определения выпуклого конуса. Пусть векторы .Согласно определению 1 найдутся такие, что при всех и при всех . Таким образом, оба неравенства справедливы при всех ,где . В силу выпуклости функции имеем

.

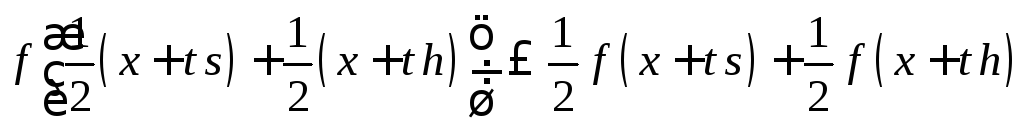Следовательно, 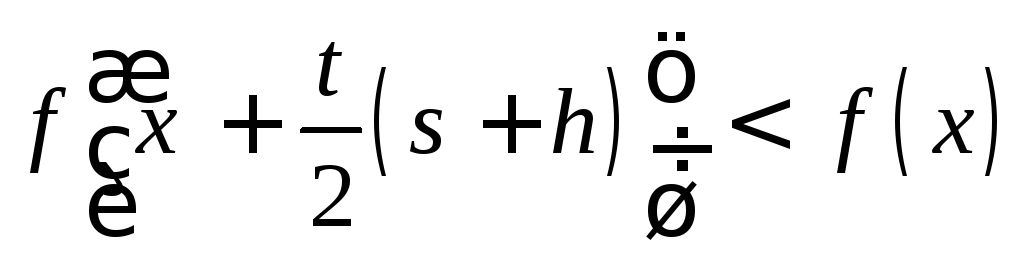,то есть при всех , где . Итак, . Что и требовалось.

Релаксационные направления часто используются как при исследовании задач на минимум, так и в различных методах численного решения оптимизационных задач. В случае, когда решается задача максимизации, используютсянаправления возрастания функции в точке, удовлетворяющие неравенству при .

Определение 1 не всегда позволяет непосредственно отыскивать релаксационные направления функции или устанавливать их отсутствие. Для выпуклых дифференцируемых функций в этом может помочь следующая теорема.

Теорема 2.Пусть – выпуклая дифференцируемая в точкефункция. Тогда

. (1)

Доказательство. Докажем сначала включение во множество. Пусть . Тогда существуеттакое, что,. Из теоремы 4.1 получаем. Из этих двух неравенств и следует. Что и требовалось.

Докажем обратное включение. Пусть имеет место неравенство . Так как по условию функция дифференцируема в точке , имеем, где. Поэтому, для достаточно малых знак приращения функции совпадает со знаком произведения. Тогда существуеттакое, что,, то есть. Что и требовалось.

Заметим, что при доказательстве второго включения выпуклость функции не использовалась.

Заметим также, что в условиях теоремы 2 при конус является открытым полупространством.

Наконец, легко увидеть, что если функция вогнута и дифференцируема в точке , то вектор является направлением возрастания функции в точке тогда и только тогда, когда выполняется неравенство .

В случае, когда функция линейна (), а значит, выпукла и вогнута одновременно, неравенствозадает конус направлений убывания, а– конус направлений возрастания в любой точке.

Определение 2.Пусть – множество из, точка. Векторназываетсявозможным направлением в точке для множества, если существует числотакое, чтодля любого.

Обозначим множество возможных направлений в точке для множества через .

Теорема 3.Пусть – выпуклое множество,. Тогда– выпуклый конус.

Доказательство. Пусть вектор ,число .Тогда согласно определению 1 имеем для любого ,то есть вектор .

Проверим теперь выполнение второго требования определения выпуклого конуса. Пусть векторы .Согласно определению 2 найдутся такие, что при всех и при всех . Таким образом, эти включения справедливы при всех ,где . В силу выпуклости множества имеем , то есть при всех , где . Таким образом, . Что и требовалось.

Заметим, что если , то .

Теорема 4.Если–выпуклое множество, точки, то вектор.

Справедливость этого утверждения непосредственно следует из определений выпуклого множества и возможного направления.

При исследовании задач на условный экстремум нам понадобятся так называемые условно релаксационные направления.

Определение 3.Пусть функция определена на множестве, точка. Векторназываетсяусловно релаксационным направлением функции в точкеотносительно множества, если в этой точке направлениеявляется возможным дляи релаксационным для функции.

Обозначим множество условно релаксационных направлений функции в точке через .Итак,, а значит, в условиях теорем 1 и 3 множествоявляется выпуклым конусом.