Моп_Л3ИНФ_Л7ПМ_2с

Файл Моп_Л3_2сИНФ.doc совпадает с Моп_Л7_2сПМ.doc = "Прямые методы условной оптимизации-Лекц1.doc" из А.Г.Трифонов. "Постановка задачи оптимизации и численные методы ее решения" 3. Методы условной оптимизации. I:\RES_H\WORK\EDUCATION\ХНУРЭ - учебные курсы\МЕТОДЫ ОПТИМИЗАЦИИ\MO\MO\NewLab20807\Doc\MProection\Метод проекций гр.doc

Прямые методы условной оптимизации

Лекция 3 (ИНФ-желательно, после 1-й консультации) = Лекция 7 ПМ

В общем случае численные методы решения задач нелинейного программирования можно разделить на прямые и непрямые. Прямые методы оперируют непосредственно с исходными задачами оптимизации и генерируют последовательности точек {x[k]}, таких, что f(х[k+1]) < f(x[k]). Здесь в [] – индекс. В силу этого такие методы часто называют методами спуска.

Математически переход на некотором k-м шаге (k 0, 1, 2, ...) от точки х[k] к точке x[k+1] можно записать в следующем виде:

x[k+l] x[k] + a_kp[k],

где р[k] — вектор, определяющий направление спуска;

а_k — длина шага вдоль данного направления.

При этом в одних алгоритмах прямых методов точки х[k] выбираются так, чтобы для них выполнялись все ограничения задачи, в других эти ограничения могут нарушаться на некоторых или всех итерациях. Таким образом, в прямых методах при выборе направления спуска ограничения, определяющие допустимую область G, учитываются в явном виде.

Ранее рассмотренные непрямые методы сводят исходную задачу нелинейного программирования к последовательности задач безусловной оптимизации некоторых вспомогательных функций. К ним относятся методы функции Лагранжа и штрафных функций, рассмотренные на прошлых лекциях. Рассмотрим теперь основные алгоритмы прямых методов.

Метод проекции градиента

Проведем сначала «правдоподобные рассуждения» и рассмотрим алгоритм данного метода применительно к задаче оптимизации с ограничениями-неравенствами. В качестве начальной выбирается некоторая точка допустимой области G. Если х[0] - внутренняя точка множества G

(Рис. 1), то рассматриваемый метод является обычным градиентным методом:

x[k+l] x[k] –a_kf’(x[k]), k 0, 1, 2, ...,

где 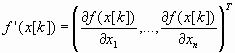градиент целевой функции f(х) в точке x[k].

После выхода на границу области G в некоторой граничной точке х[k] , k 0, 1, 2,..., движение в направлении антиградиента -f’(х[k]) может вывести за пределы допустимого множества (см. Рисунок 1). Поэтому антиградиент проецируется на линейное многообразие М, аппроксимирующее участок границы в окрестности точки х[k]. Двигаясь в направлении проекции вектора -f'(x[k]) на многообразие М, отыскивают новую точку х[k+1], в которой f(х[k+1]) f(x[k]), принимают х[k+1] за исходное приближение и продолжают процесс. Проведем более подробный анализ данной процедуры.

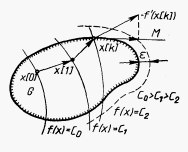
Рисунок 1.

Геометрическая интерпретация метода проекции градиента

В точке х[k] часть ограничений-неравенств удовлетворяется как равенство:

h_j(x) 0, j 1, ..., l; l < m. Такие ограничения называют активными.

Обозначим через J набор индексов j (1 j l) этих ограничений. Их уравнения соответствуют гиперповерхностям, образующим границу области G в окрестности точки х[k] . В общем случае эта граница является нелинейной (см. рис.1). Ограничения h_j(x), j J, аппроксимируются гиперплоскостями, касательными к ним в точке х[k]:

Полученные гиперплоскости ограничивают некоторый многогранник М, аппроксимирующий допустимую область G в окрестности точки х[k] (см. Рис. 1).

Проекция р[k] антиградиента -f'(x[k]) на многогранник вычисляется по формуле p[k]  [-f’(x[k])].

Здесь  - оператор ортогонального проектирования, определяемый выражением  E – A^T(AA^T)^-1A, (1)

где Е - единичная матрица размерности пп;

А - матрица размеров l  n . Она образуется строками – транспонирован­ными вектор-столбцами градиентов активных ограничений из множества J: а_j=(h_j)^T, j 1, ..., l.

( Здесь x[k]Г(G) является началом координат, из которого проводится радиус-вектор f. Значит b=0, и это – проекция на подпространство, а не на многообразие ).

Далее осуществляется спуск в выбранном направлении: x[k+1] x[k] + _kp[k]. Можно показать, что точка х[k+1] является решением задачи минимизации функции f(х) в области G тогда и только тогда, когда [-f’(x[k])] 0. Из (1) [-f (x[k])]= -f (х[k]- A^T{ (AA^T)^-1A(-f (х[k]))}= -f (х[k])-a_ju_j=0.

Это – необходимое условие 1-го порядка для функции Лагранжа, т.е., вектор-столбцы -f(х[k])=a_ju_j , где множители Лагранжа u положительны, по условию Куна-Таккера. u (u₁, ..., u_l)^Т (AA^Т)^-1A(-f (х[k])) > 0.

Эти условия означают, что антиградиент (-f (х[k])) целевой функции является линейной комбинацией с неотрицательными коэффициентами градиентов активных ограничений h_j(x) 0. Напомним, что h есть нормаль касательной гиперплоскости.

В соответствии с изложенным, алгоритм метода проекции градиента состоит из следующих операций.

1. В точке х[k] определяется направление спуска р[k].

2. Находится величина шага _k.

3. Определяется новое приближение х[k+1].

Рассмотрим детально каждую из этих операций.

1. Определение направления спуска состоит в следующем. Пусть найдена некоторая точка х[k] G и известен набор активных ограничений h_i(х[k]) 0, j J. На основании данной информации вычисляют (-f (х[k])) и определяют проекцию  [-f (х[k])]. При этом возможны два случая:

а)  [-f’(х[k])] не равна 0. В качестве направления спуска р[k] принимают полученную проекцию;

б)  [-f (х[k])] 0, т. е. -f(х[k])=a_ju_j

Данное выражение представляет собой систему из п уравнений для определения коэффициентов и_j. Если все и_j 0, j J, то в соответствии с вышеизложенным точка х[k] является решением задачи. Если же некоторый компонент и_q 0, то соответствующий ему градиент выводится из матрицы А и порождается новая проецирующая матрица . Она определит новое направление спуска.

2. Для определения величины шага _k целевая функция минимизируется по направлению р[k] при условии соблюдения ограничений задачи с установленной точностью. Последняя задается введением некоторого положительного числа . Считают, что точка х удовлетворяет условиям задачи с заданной точностью, если h_i(х) , j 1, ..., m. Величина шага _k определяется решением задачи вида:

f(x[k] + р[k])  min;

h_j(x[k] + р[k]) , j 1, ..., m.

3. Определение нового приближения состоит в том, что очередная точка вычисляется по формуле

x[k+1] x[k] + _k р[k].

Признаком сходимости является стремление к нулю векторов р[k].

Внимание! Для выпуклой области проекция на аппроксимирующий многогранник не принадлежит области.

Рассмотренный метод является в некотором смысле аналогом градиентных методов для решения задач на безусловный экстремум, и ему свойствен их недостаток - медленная сходимость.

Приведем несколько утверждений, обосновывающих метод и оценивающих скорость его сходимости (изложение согласно книге: Сухарев и др. – Курс методов оптимизации)

Рассмотрим элементы теории метода проекции градиента для решения задачи следующего вида: (2)

где  - замкнутое выпуклое множество в , дифференцируемая функция на . Пусть является оптимальным решением задачи (2).

Напомним вначале свойства проекции точки на множество.

Проекцией точки на множество называется точка такая, что , т.е. точка, ближайшая к a среди всех точек из X. Если , то , если X замкнуто. Если же a не принадлежит X, и X - открыто, то проекция не существует.

Из определения следует, что является решением следующей задачи оптимизации: .

Лемма 1 Пусть замкнутое выпуклое множество в . Тогда

1. Проекция любой точки существует и единственна;

2. Точка является проекцией точки a на множество X в том и только в том случае, если

3. Для всех точек справедливо неравенство

т.е. оператор проектирования обладает свойством нерастяжения расстояний.

Доказательство леммы приведено в [Сухарев, с. 225].

Сформулируем необходимое и достаточное условие оптимальности для выпуклой задачи.

Лемма 2. Пусть множество X выпукло и замкнуто, функция f выпукла на X и дифференцируема в точке . Тогда является решением задачи (2) в том и только в том случае, если

при произвольном .

Доказательство леммы приведено в [Сухарев, с. 226].

Теперь рассмотрим алгоритм метода проекции градиента и его сходимость. В методе проекции градиента в качестве очередной точки приближения к решению задачи (2) выбирается проекция точки на множество X той точки, которая получается по градиентному методу:

, где (3)

Коэффициенты можно выбирать различными способами. (см. например, книги: Сухарев и др. или Реклейтис и др.). Рассмотрим теорему о сходимости проекции градиента с априорным выбором коэффициентов , то есть последовательность выбирают заранее, до начала вычислений (например, , где k=0,1,2,...).

Теорема 1. Пусть множество X выпукло и замкнуто, функция f сильно выпукла с константой и дифференцируема на X, причем ее градиент удовлетворяет условию Липшица:

Тогда последовательность , генерируемая по формуле (3), где произвольная точка из X, а сходится к решению задачи (2) со скоростью геометрической прогрессии:

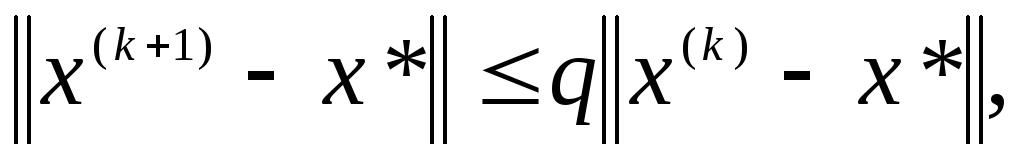
где

Доказательство теоремы приведено в [Сухарев, с. 226].

Замечания:

1. В рассмотренном методе на каждой k-ой итерации требуется производить операцию проектирования точки на множество X, то есть решать задачу вида (2) при 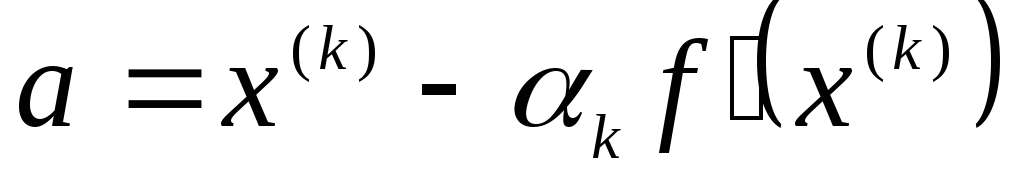. В некоторых случаях удается указать явный вид проекции, например, если множество X  шар, координатный параллелепипед, полупространство, гиперплоскость, аффинное множество. Однако, если X задается с помощью более или менее сложной системы равенств и неравенств, то метод проекции градиента практически неприменим, так как задача поиска проекции оказывается не проще исходной.

2. Константы 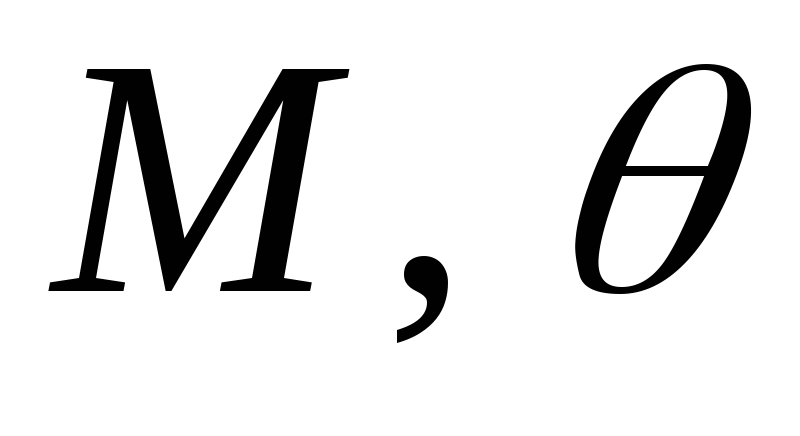из теоремы 1 обычно неизвестны, что затрудняет отыскание . Тогда можно использовать другие правила выбора длины шага, например, различные модификации метода наискорейшего спуска с приближенным решением задач одномерной минимизации по или правило дробления шага [Реклейтис и др.].

3. Используя идею проектирования, можно модифицировать применительно к задачам условной оптимизации и другие методы безусловной оптимизации, в том числе метод Ньютона и метод сопряженных направлений.

Пример: Решить методом проекции градиента:

.

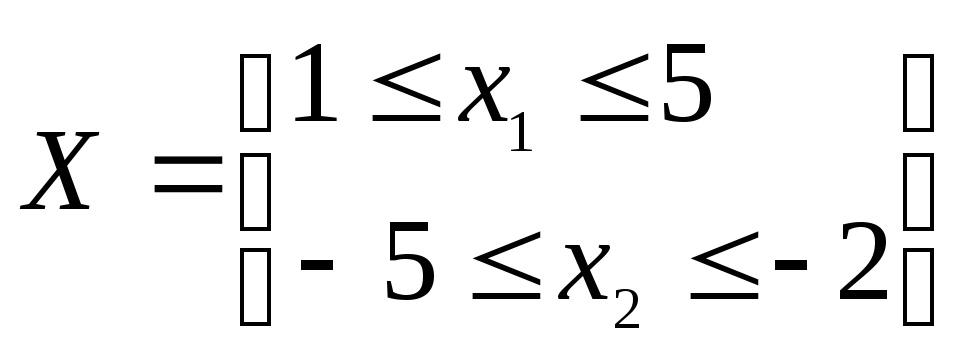Решение. Используем соотношение (3). Выберем начальное приближение . Пусть шаг в выражении (3) равен . Критерий останова выберем следующий: , где .

Итерация 1. В соответствии с выражением (3) определяем .

, .

Точка выходит за пределы области X. Так как множество X – коорди­натный параллелепипед, то можно указать явный вид проекции точки на множество. Известно, что если – координатный параллелепипед, то : 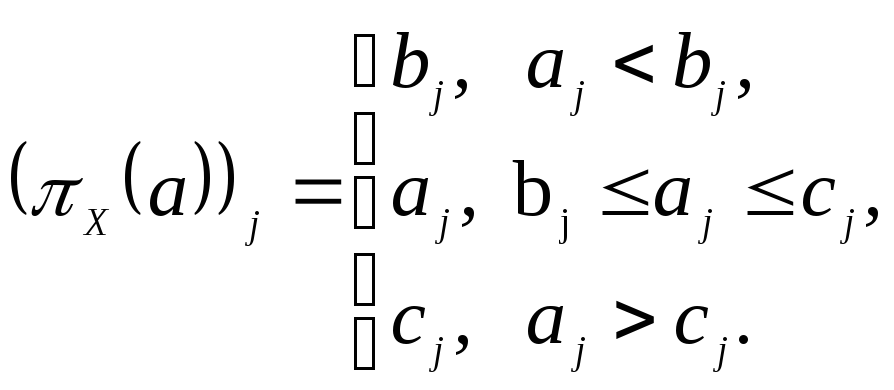(см.[Сухарев, с.227], а также лекцию о проекциях (Консультация №1).

В нашем случае , .

Так как , то проверяем критерий останова: . Критерий останова не выполняется, значит, переходим к следующей итерации.

Итерация 2. В соответствии с выражением (3) определяем

.

, .

Точка выходит за пределы области X.

Значит, , . .

Критерий останова выполняется, значит, процесс вычислений закончен.

Методы отсекающих плоскостей ( Реклейтис т1 стр. 329 ). Метод Келли

Изложим основные моменты метода Келли, описав последовательность действий при его работе.

Пусть функция цели ‑ линейная. Рассмотрим следующую задачу:

, , (4)

где K‑ выпуклое множество. Замечание: если ограничения x_i ≥ 0 активны, то функции g_i(x) – вогнуты.

Алгоритм решения задачи (4) состоит в следующем:

1. Задать множество .

Решить задачу . (5)

Задача (5) представляет собой задачу линейного программирования. Для ее решения необходимо использовать методы решения ЗЛП (например, симплекс-метод). Пусть ‑ решение задачи (5).

Для k=1,2,… выполнить следующую последовательность шагов.

2. Вычислить индекс следующим образом:

, где ‑ решение задачи на k-й итерации. Т.е., p – индекс наиболее удаленного ограничения. Проверить условие окончания вычислений: если , то прекратить вычисления. В противном случае перейти к пункту 3.

3. Построить отсекающую плоскость следующего вида:

. (6)

Пусть ‑ полупространство вида:

.

Сформулировать новую систему ограничений вида: . Решить задачу линейного программирования вида:

.

Перейти к пункту 2.

Подставим в (6) x:= x^(k) . , значит x^(k) H^(k). g_p по условию, вогнутая, и . То есть, во всех точках xK. Значит, K H^(k). Гиперплоскость (6) действительно отсекает x* от K, и для выпуклых

K получаем систему вложенных множеств K^(k+1)  K^(k), стягивающуюся к K.

В случае, если нелинейная функция, то вместо задачи

,

рассматривается задача

, . (7)

Таким образом, (7) представляет собой задачу с линейной функцией цели.

Особенности метода:

1. Генерация минимизирующей последовательности 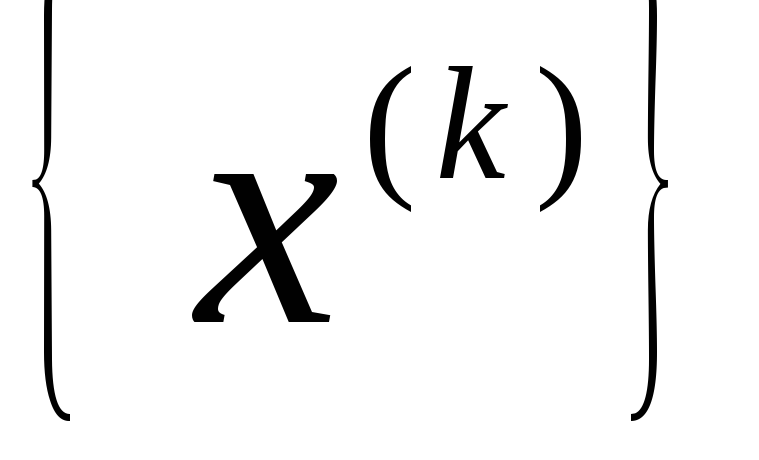в методе Келли осуществляется таким образом, что каждая из точек 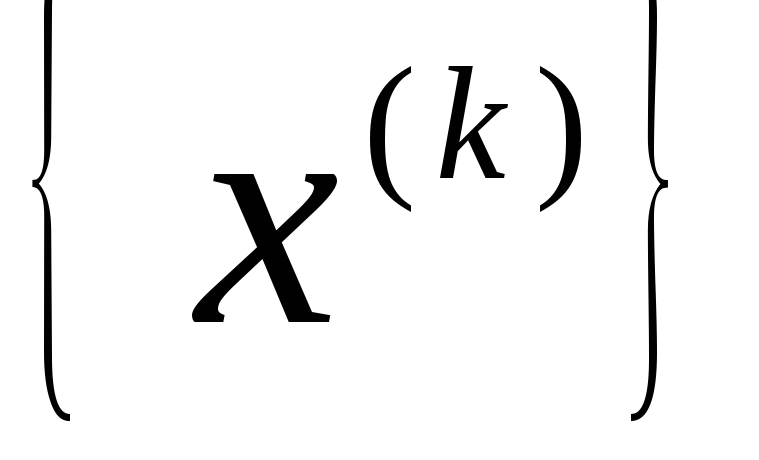является недопустимой точкой, то есть 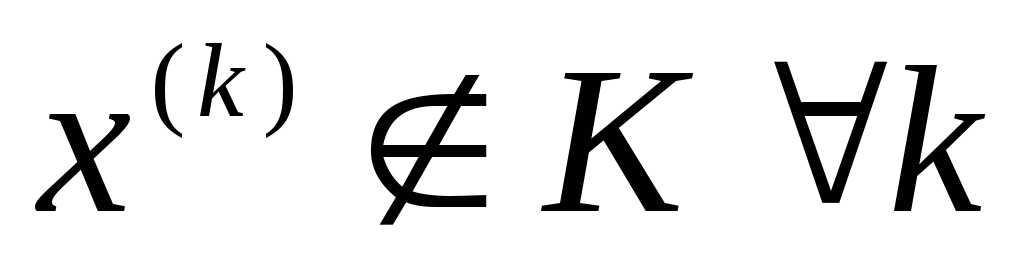. Это является одним из недостатков метода Келли и приводит к тому, что процесс вычисления нельзя останавливать даже при достаточно больших k.

2. Сходимость к оптимальному решению по функционалу метод Келли гарантирует в том случае, если 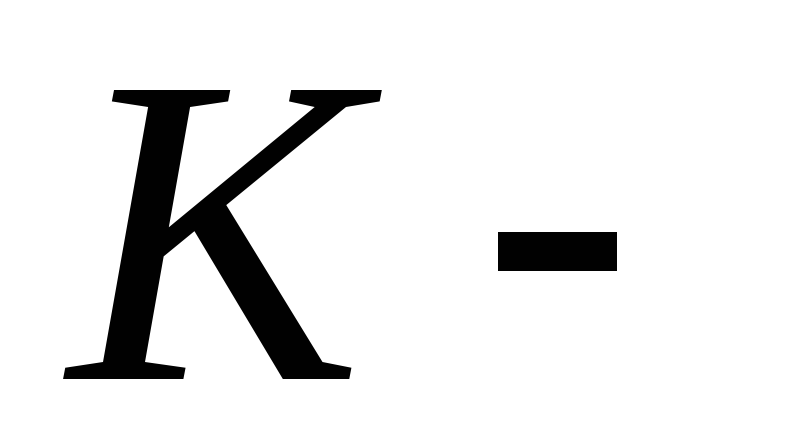выпуклая область.

3. Последовательность областей 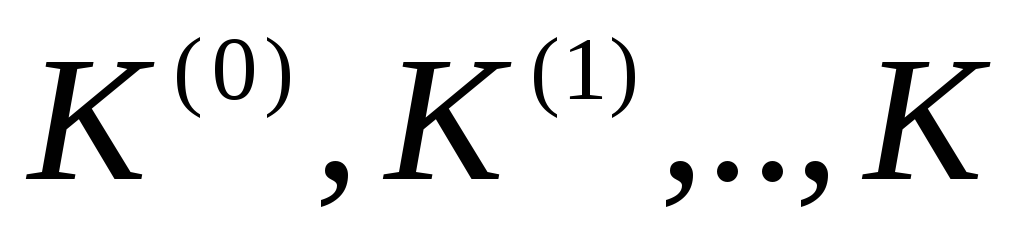представляет собой семейство вложенных множеств. Если это свойство выполняется 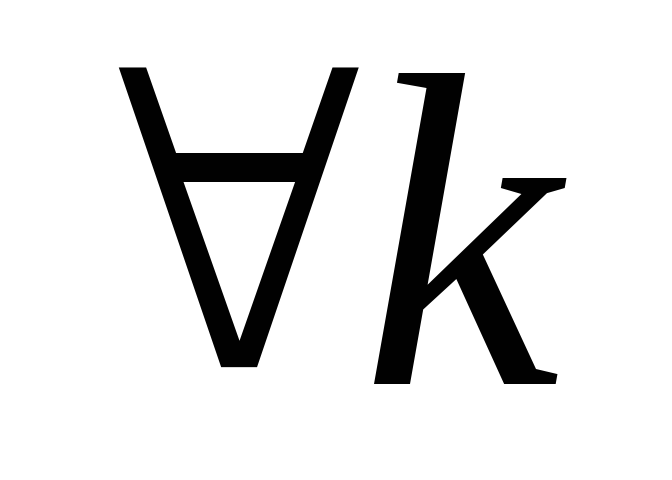, то при этом не происходит потери части допустимой области, что возможно, если множество K невыпукло.

4. С увеличением количества итераций k растет размерность задачи линейного программирования. Кроме того, при приближении к решению отсекающие плоскости начинают практически совпадать, что затрудняет решение задачи. Использование процедуры отбрасывания плоскостей позволяет уменьшать размерность задачи, но отбрасывать можно лишь те ограничения, которые не являются активными для оптимального плана предыдущей задачи.

Пример. Решить методом Келли следующую задачу: [ Реклейтис т.1, с. 333-335 ]

,

.

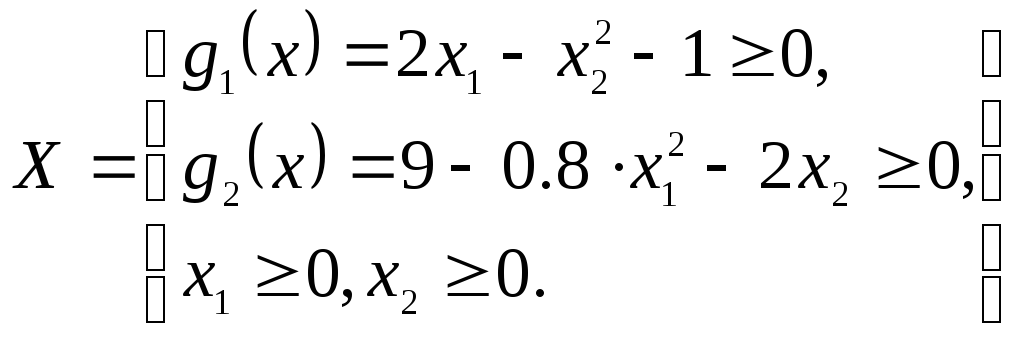Как видно из Рисунка 2, допустимая область этой задачи лежит в прямоугольнике . Функции и вогнутые. Зафиксировав некоторое малое , перейдем к пункту 1 алгоритма, полагая .

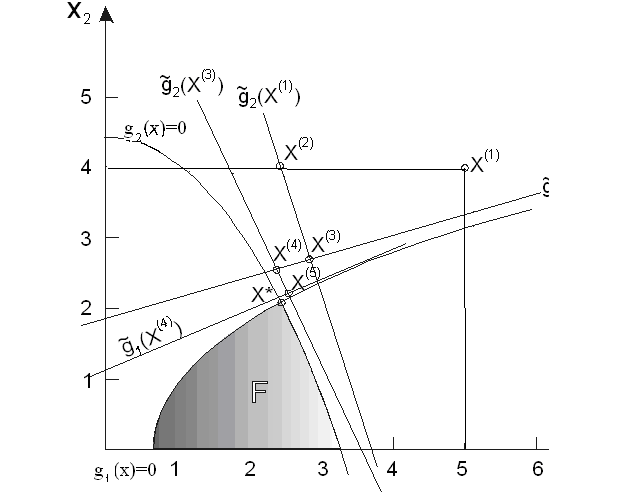
Рисунок 2

Итерация 1. Найдем минимум функции при ограничениях , .

Очевидно, что решением является точка .

Поскольку , , наиболее сильно нарушается ограничение . Значит, p=2.

Отсекающая плоскость задается при помощи линеаризации в точке , так что .

Таким образом, необходимо добавить ограничение . Заметим, что точка не удовлетворяет этому ограничению. Теперь следует решить подзадачу:

, (8)

. (9)

Оптимальная точка задачи (8)-(9): .

Итерация 2. , . Ясно, что первое ограничение нарушается сильнее, причем величина невязки велика, поэтому необходимо продолжать выполнение итераций алгоритма.