Моп_Л3_2сПМ.doc Методы оптимизации 2 из "I:\RES_H\WORK\EDUCATION\ХНУРЭ - учебные курсы\МЕТОДЫ ОПТИМИЗАЦИИ\II семестр\ЗАГОТОВКИ\Лекции\REVIZED\"

Лекция 3 (ПМ-СА)

Элементы выпуклого анализа

Выпуклый анализ – это раздел современного математического анализа, посвященный изучению выпуклых множеств и выпуклых функций. Приведем основные сведения из выпуклого анализа необходимые для изучения теории и методов решения экстремальных задач.

1. Выпуклые множества

Определение 1. Пусть заданы точки и любое . Линейная комбинация называется выпуклой комбинацией точек и .

Часто выпуклую комбинацию записывают в виде или . Легко увидеть, что эти формы записи эквивалентны.

Определение 2. Множество всех выпуклых комбинаций точек называется отрезком прямой, соединяющим эти точки.

Определение 3. Множество называется выпуклым, если отрезок включается в для любых .

Теорема 1. Пусть имеется семейство выпуклых множеств . Тогда множество является выпуклым.

Доказательство. Пусть , тогда . Так как все множества – выпуклые, , откуда . Таким образом, . Что и требовалось.

Прежде чем сформулировать следующую теорему, напомним определение операций сложения множеств и умножения множества на число. Для множеств и чисел

.

Теорема 2. Пусть для всех множества – выпуклые, . Тогда выпукло и множество .

Доказательство. Пусть , тогда существуют такие векторы , что , . Пусть . Так как все множества являются выпуклыми, то для любого имеем включение .

Следовательно, ,

что и означает выпуклость множества .

Теорема 3. Пусть – выпуклое множество, тогда его замыкание также выпукло.

Доказательство. Пусть , то есть – предельные точки множества . Тогда существуют последовательности такие, что , .

Пусть – любое из отрезка . Тогда

В силу выпуклости множества выполняются включения Следовательно, , что и означает выпуклость множества .

Теорема 4. Пусть – выпуклое множество, тогда его внутренность также выпукла.

Выше было приведено определение выпуклой комбинации двух векторов. Обобщим это понятие на случай произвольного конечного числа векторов.

Определение 3. Линейная комбинация векторов называется выпуклой комбинацией, если , и .

Определение 4. Множество всевозможных выпуклых комбинаций любого конечного числа векторов из множества называется выпуклой оболочкой множества и обозначается

Очевидно, что для всякого множество является выпуклым. Нетрудно показать, что множество является выпуклым тогда и только тогда, когда

Возможен и другой подход к определению выпуклой оболочки множества. Выпуклой оболочкой множества называется наименьшее выпуклое множество, содержащее , то есть пересечение всех выпуклых множеств, содержащих . Эти определения выпуклой оболочки эквивалентны.

Определение 5. Вектор из выпуклого множества называется крайней точкой множества , если он не является выпуклой комбинацией никаких двух других векторов из .

Легко увидеть, что любая крайняя точка выпуклого множества является его граничной точкой, но не всякая граничная точка является крайней.

2. Выпуклые конусы

Определение 1. Множество называется выпуклым конусом, если

1. для любых 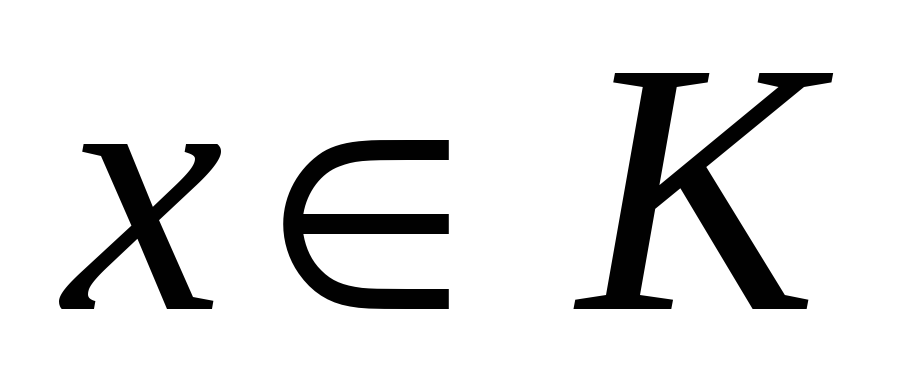и 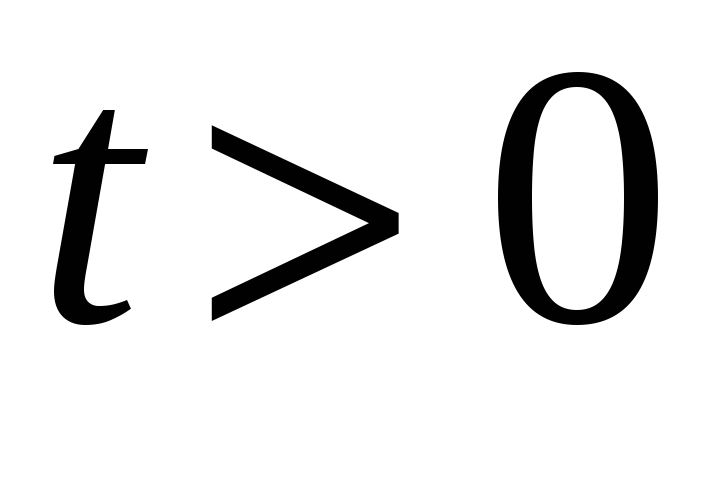выполняется включение ,

2. для любых 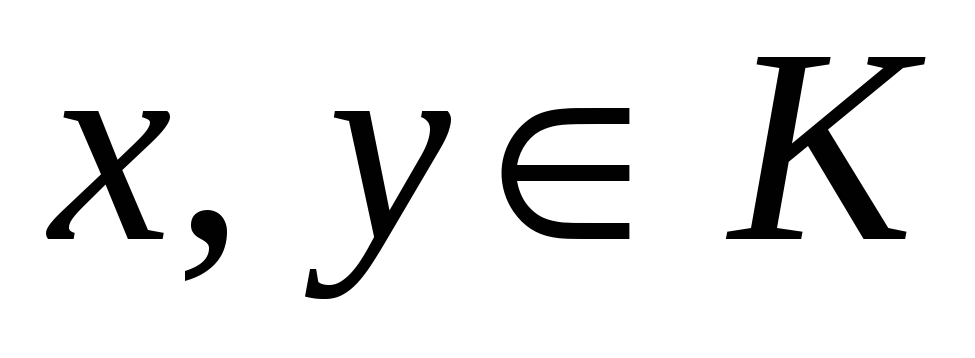выполняется включение .

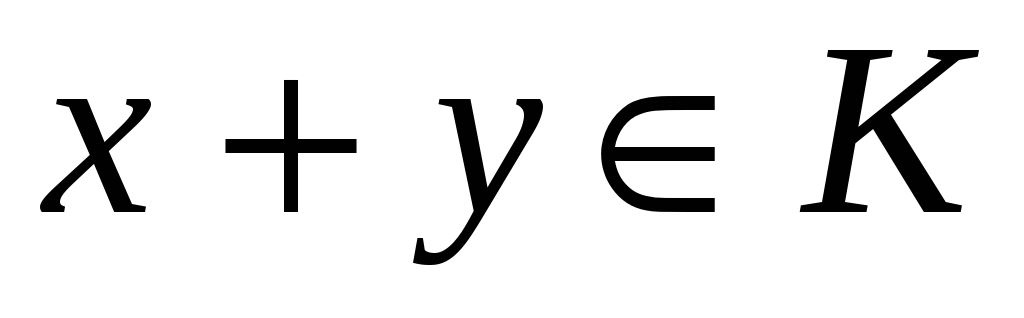Легко убедиться в справедливости следующей теоремы.

Теорема 1. Выпуклый конус является выпуклым множеством.

Следующие 4 теоремы устанавливают некоторые операции допустимые в классе выпуклых конусов. (Рекомендуем доказать теоремы 2 – 4 самостоятельно.)

Теорема 2. Пусть имеется семейство выпуклых конусов . Тогда множество является выпуклым конусом.

Теорема 3. Пусть – выпуклые конусы. Тогда множество 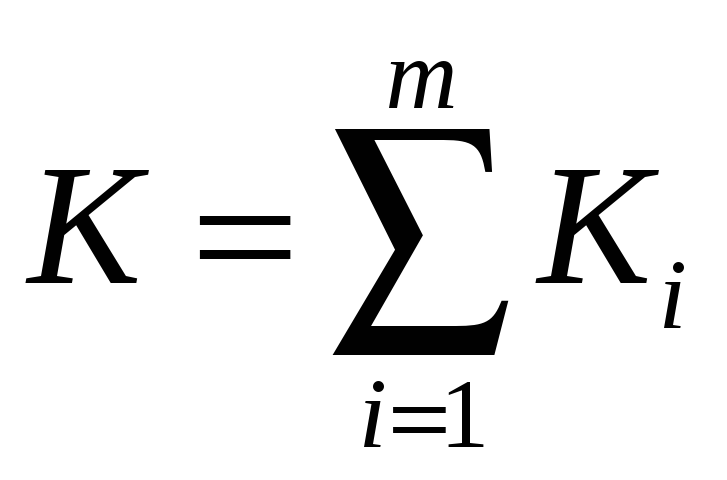также выпуклый конус.

Теорема 4. Пусть – выпуклый конус. Тогда замыкание – также выпуклый конус.

Теорема 5. Пусть – выпуклый конус. Тогда также выпуклый конус.

Легко увидеть, что нулевой вектор пространства является предельной точкой любого выпуклого конуса. Вектор 0 называется вершиной выпуклого конуса. Выпуклый конус может иметь не более одной крайней точки и этой крайней точкой может быть только вершина конуса.

Определение 2. Линейная комбинация векторов , называется конической комбинацией, если . (Здесь =1 не требуется)

Определение 3. Множество всевозможных конических комбинаций любого конечного числа векторов из множества называется конической оболочкой множества и обозначается .

Очевидно, что для всякого множества множество является выпуклым конусом.

Определение 4. Пусть – ненулевой вектор. Множество называется лучом, а вектор называется направляющим вектором этого луча.

Очевидно, что луч – вырожденный случай выпуклого замкнутого конуса.

Определение 5. Пусть – выпуклый конус. Луч называется крайним лучом, если он не принадлежит конической оболочке двух других лучей этого конуса.

Легко увидеть, что любой крайний луч выпуклого конуса принадлежит его границе, но не всякий луч, принадлежащий границе, является крайним лучом.

3. Выпуклые функции

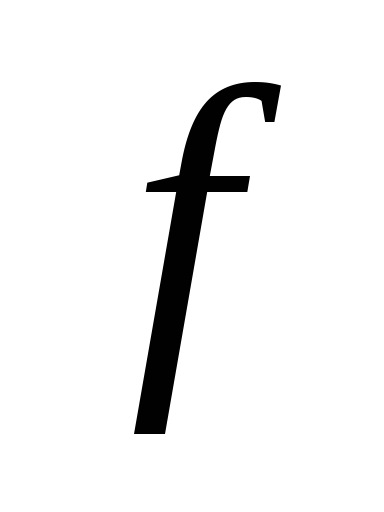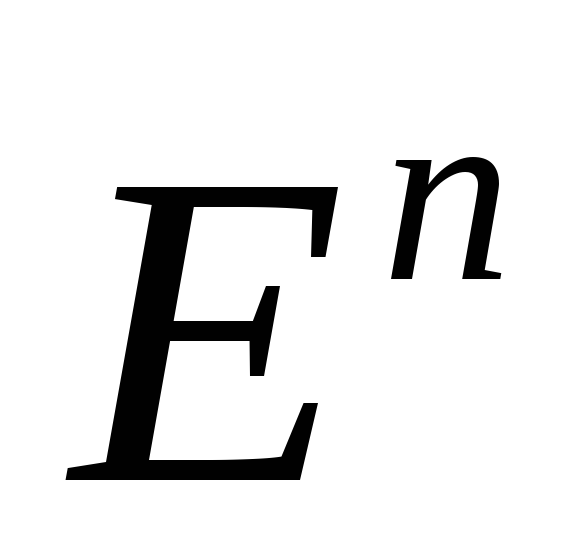Определение 1. Функция , определенная на , называется выпуклой, если для любых 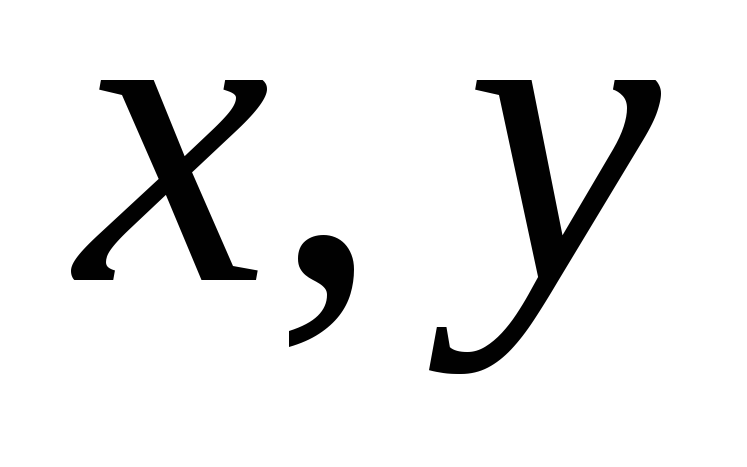и любого 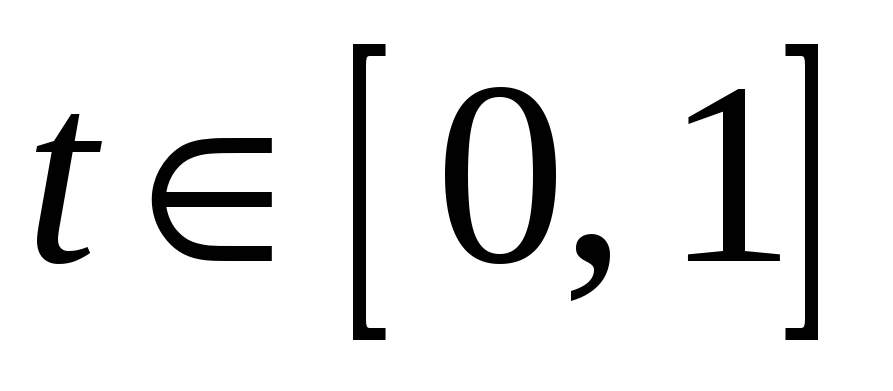выполняется неравенство

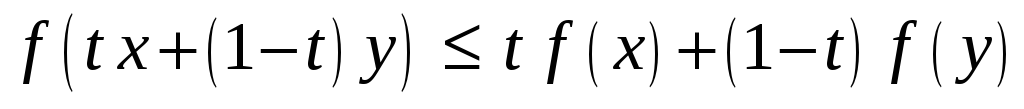. (1)

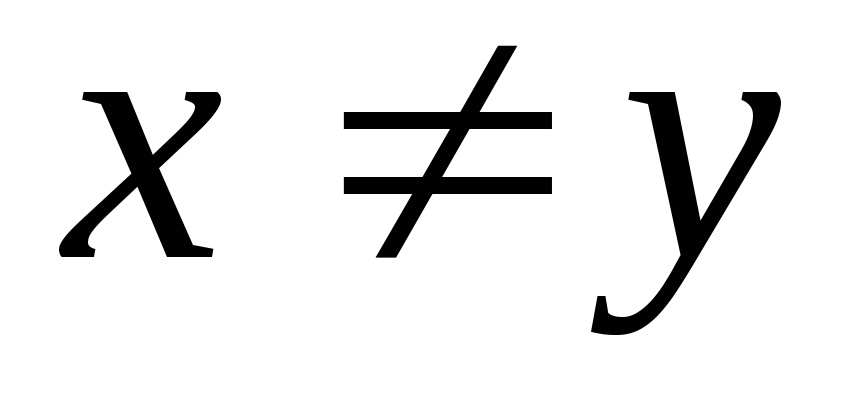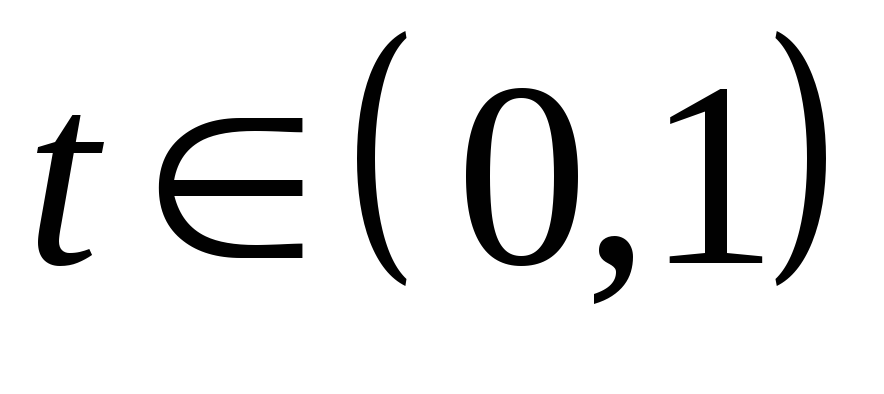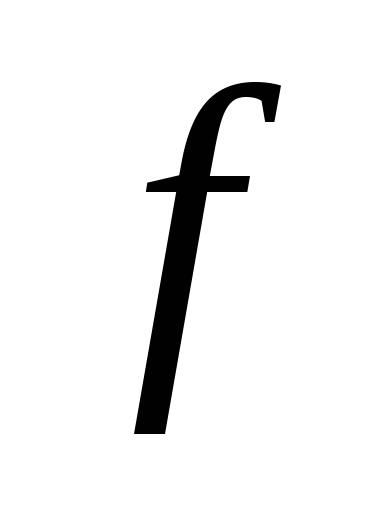Если при и неравенство (1) выполняется как строгое, то функция называется строго выпуклой.

Определение 2. Функция , определенная на , называется вогнутой (строго вогнутой), если функция () является выпуклой (строго выпуклой).

Очевидно, что любая строго выпуклая (строго вогнутая) функция является выпуклой (вогнутой) функцией, но не наоборот.

Приведем некоторые операции допустимые в классе выпуклых функций.

Теорема 1. Пусть все функции , ,

выпуклы на , числа . Тогда функция также выпукла.

Доказательство. Пусть заданы векторы и число . Так как функции , выпуклы, то для всех выполняются неравенства

. Умножая эти неравенства на неотрицательные величины и суммируя их по , получим неравенство

.

Следовательно, . Что и требовалось.

Теорема 2. Пусть на определены функции

, . Если все – выпуклые, то функция также выпуклая.

Доказательство. Пусть заданы векторы и число . Так как функции выпуклы, то для всех выполняются неравенства

. Следовательно,

для всех . Из полученных неравенств имеем

то есть . Что и требовалось.

Приведем теоремы о суперпозициях выпуклых функций.

Теорема 3. Пусть функция определена на отрезке и является на нем выпуклой и неубывающей; функция выпукла на выпуклом множестве , , для всех . Тогда функция выпукла на .

Доказательство. Пусть , . Тогда в силу выпуклости функции на . Очевидно, что . Поэтому, а также в силу монотонности и выпуклости на , имеем

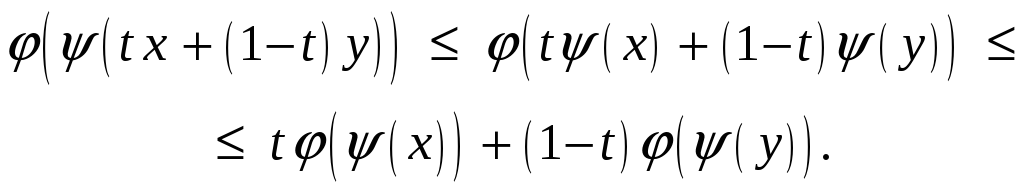
Следовательно, . Что и требовалось.

Теорема 4. Пусть – матрица размерности , – вектор размерности , – функция, определенная и выпуклая на многообразии

, . Тогда функция выпукла на .

Доказательство. Пусть заданы векторы и число . Тогда имеем

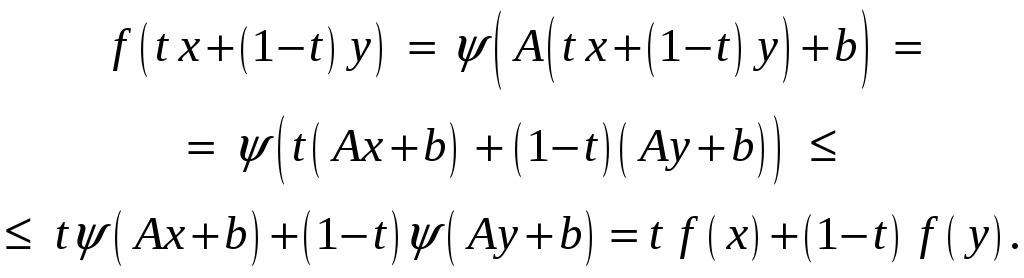
Что и требовалось.

Далее покажем, что выпуклость функции многих переменных можно установить, исследуя на выпуклость ее сужения на всевозможные прямые в . Выпуклость функции одной переменной установить зачастую значительно проще, чем выпуклость функции многих переменных.

Пусть заданы функция и векторы . Сужение функции на прямую определим следующим образом:

. (2)

Теорема 5. Функция является выпуклой тогда и только тогда, когда выпуклой является и функция , определенная по формуле (2) при любых .

Доказательство. Необходимость. Пусть – выпуклая функция, . Покажем, что функция также является выпуклой. Пусть . Тогда

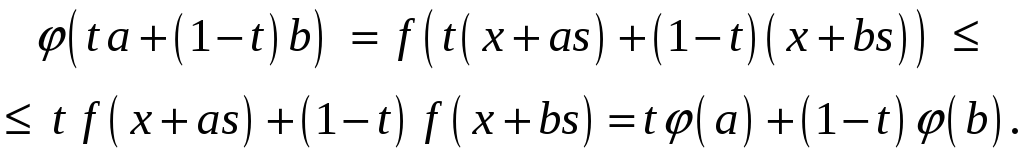
Достаточность. Предположим, что для произвольных функция – выпуклая. Пусть и . Тогда

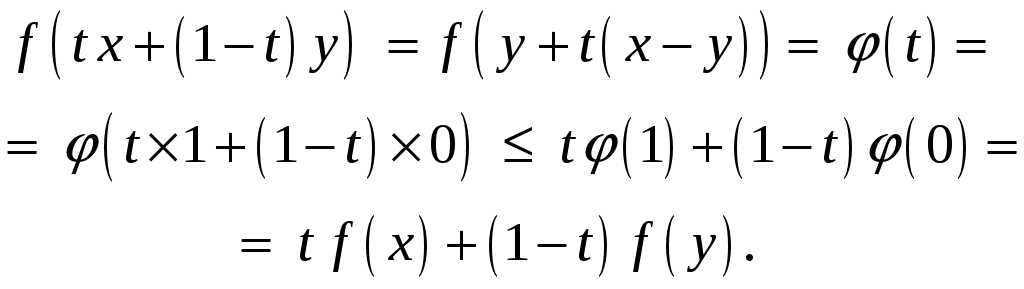
Что и требовалось.

Далее установим связь между выпуклыми множествами и выпуклыми функциями.

Пусть – некоторая константа. Множество называется лебеговым множеством функции .

Теорема 6. Пусть функция выпукла на . Тогда любое ее лебегово множество выпукло.

Доказательство. Пусть , . Тогда из и в силу выпуклости

.

Таким образом, , что и означает выпуклость множества .

Эта теорема устанавливает одностороннюю связь между выпуклыми множествами и выпуклыми функциями. Утверждение, обратное теореме 6, не имеет места.

7