4. Классическая задача условной оптимизации и методы ее решения

Переобозначим переменные согласно [1]. Классическая задача условной оптимизации в новых обозначениях имеет вид:

(3)

(4)

Итак, область допустимых решений (ОДР) в рассматриваемой задаче представляет собой некоторое многообразие коразмерностиm.

Задачу можно решить методом исключения (подстановки), решив уравнение (4) относительно (базисных) переменных _i, i=1,…m, и подставляя найденное решение в (3). Например, . Исходная задача (3), (4), таким образом, преобразована в задачу безусловной оптимизации функции. Такая операция для нелинейных функций из (4) не всегда выполнима, и всегда трудоемка.

Метод множителей Лагранжа (ммл). Необходимые условия в классической задаче условной оптимизации. Функция Лагранжа

ММЛ позволяет исходную задачу классической условной оптимизации (3), (4) преобразовать в задачу безусловной оптимизации для специально "сконструированной" функции, называемой функцией Лагранжа:

, (5)

где - множители Лагранжа;. (6)

Читатель уже знакомился с понятием функции Лагранжа в других курсах, поэтому кратко изложим лишь основные факты.

Пусть задача (3), (4) имеет локальное решение , и вектор-функция (6) удовлетворяетусловию Якоби, то есть - числу строк в матрице Якоби и числу ограничений в (6). Это часто называют условиемрегулярности. В противном случае, в L(x,) присутствует множитель _при F(x).

Перенумеруем переменные x так, чтобы последний минор матрицы Якоби был ненулевым и разобьем вектор инструментальных переменных на две части, размерности n-m и m, соответственно: .

По теореме о неявной функции в окрестности систему (4) можно разрешить относительно:=f(), гдеf – вектор столбец из m функций. Тогда исходная задача сводится к задаче оптимизации без ограничений: max Ф()= maxF(,f()), необходимое условие (1) для которой состоит в следующем:

, (7)

где ,,- вектор-строки градиентов, а- матрица Якоби размерностиn(n-m). После исключения базисных переменных ограничения (4) станут тождествами от. Продифференцируем их. («Полная» производная по, как и в (7)):

, (8)

где , по условию Якоби, невырожденная (mm) матрица. Тогда из (8)

Условия (7) запишем в виде:

(9)

Очевидно, верно тождество (10)

Полагая , из (9) и (10) получим аналог необходимых условий (7) экстремума в виде(11)

Полученный результат составляет основное содержание ММЛ.

Систему уравнений (11) можно получить формально, вводя в рассмотрение специально сконструированную выше функцию Лагранжа (5).

Действительно,

, ;,,

и система уравнений (11) представлена в виде:

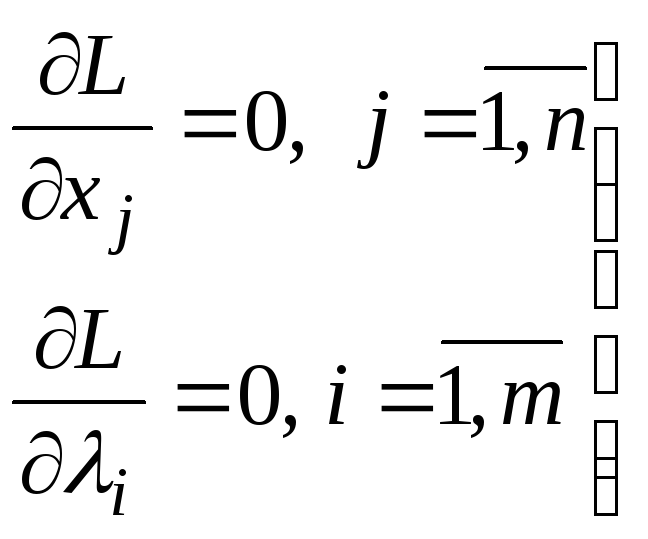(12)

Система уравнений (12) представляет необходимое условие в классической задаче условной оптимизации.

Найденное в результате решения этой системы значение вектора называетсяусловно-стационарной точкой.

Для того, чтобы выяснить характер условно-стационарной точки необходимо воспользоваться достаточными условиями.

Достаточные условия в классической задаче условной оптимизации

Эти условия позволяют выяснить, является ли условно-стационарная точка точкой локального условного минимума, или точкой локального условного максимума. Они получены подобно тому, как были получены достаточные условия в задаче на безусловный экстремум.

Результат следующий:

- точка локального условного минимума, если ;

- точка локального условного максимума, если ,

где - матрица Гессе размерности с элементами ,для функцииL() в стационарной точке. Здесь производные отL берутся только по x*, а не по всем её аргументам.

Размерность матрицы Гессе можно уменьшить, используя условие неравенства нулю якобиана:. При этом условии можно зависимые переменные (пусть здесь они стоят первыми)выразить через независимые переменные. Матрица Гессе дляL_N, полученной в результате подстановки, будет иметь размерность , т.е. необходимо говорить о матрицес элементами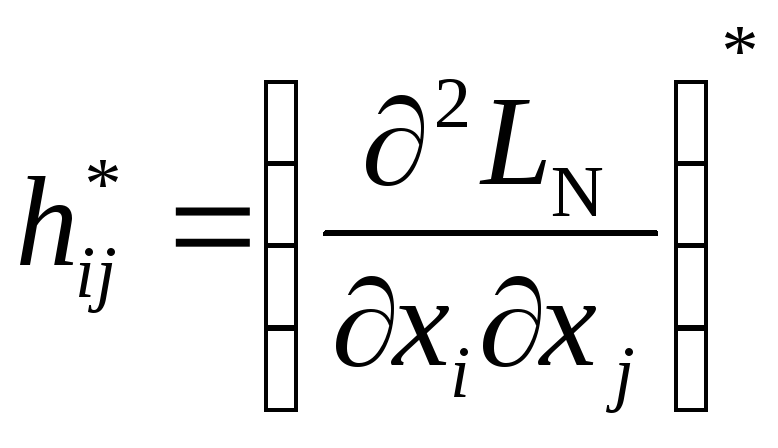,, тогда достаточные условия будут иметь вид:

, для точки локального условного минимума.

, для точки локального условного максимума.