Основним елементом обробки інформації є електронний прилад з двома стійкими електричними станами, які відповідають логічному 0 чи 1.

Тема 2. Фундаментальні основи легування напівпровідників

Теплоперенос в твердих тілах. Імпульсний нагрів н/п.

Важливу роль у процесах легування н/п відіграють теплові процеси. Наприклад, дифузія відбувається як за ізотермічного, так і за імпульсного нагріву н/п кристалу (1200-1350 К) з метою одержання необхідного концентраційного профілю домішки; після процесу іонної імплантації застосовують термічний відпал н/п з метою усунення радіаційних ефектів, а також, для розгонки імплантованої домішки.

Тепло у твердих тілах переноситься фононами і носіями струму. Ці механізми називаються відповідно фононною і електронною складовими теплопровідності. У металах, де значна концентрація вільних електронів, переважаючою є електронна теплопровідність виродженого газу. У неметалах основний внесок у теплоємність вносить енергія градкових коливань. У н/п тією чи іншою мірою проявлятимуться обидва механізми, залежно від кристалічної структури, типу хімічного зв’язку, температури кристалу та інших факторів.

Основи теорії теплоємності.

Кристал як багаточастинкова система – це ансамбль зв’язаних осциляторів. Якщо амплітуда коливань його структурних частинок << від періоду гратки, то використовується гармонійне наближення, в основі якої є осциляторна модель, яка пройшла 3 етапи:

1. класична модель незалежних осциляторів;

2. квантова модель незалежних осциляторів;

3. квантова модель зв’язаних осциляторів;

1.Згідно з класичною теорією кристали (системи з багатьох частинок) характеризуються термодинамічними потенціалами (внутрішня енергія W, вільна енергія, термодинамічний потенціал Тіббса та ентальпія), ентропією та теплоємністю.

Якщо кожен атом чи іон кристалу розглядати як класичний осцилятор, який коливається у 3 ????, то його енергія , а повна енергія кристалу з N атомів . Тоді за означенням молярна теплоємність градки при сталому об’ємі:

- закон Дюлонга-Пті (теплоємність твердих тіл не залежить від природи тіла і температури). Добре узгоджується з експериментом лише при порівняно великих температурах, в тому числі і кімнатній.

2.Для назьких температур проявляється квантовий характер коливань елементарної градки.

Енштейн розглянув кристал як сукупність незалежних квантових гармонійних осциляторів, кожен з яких здійснює коливання з частотою .

Тоді енергія ) ; розподіл фононів за енергіями описується функцією Планка з використанням статистичної суми ,

Тоді повна енергія кристалу , де враховано 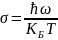. Якщо ввести параметр – температуру Енштейна, то в області високих температур (θ<< ) випливає висновок класичної теорії про незалежність теплоємності від температури, а в області низьких температур θ>> , отримаєм

, де – теплоємність зменшується, однак не прямує до нуля.

3.Дебай розглянув теплові коливання як суперпозицію нормальних коливань системи зв’язаних квантових осциляторів.

Тоді вираз для внутрішньої енергії твердого тіла:

, де , – температура Дебая.

Якщо , то , для низьких температур при , що і спостерігається есперементально.

Розглянемо процеси на поверхні твердих тіл, які є важливими у випадку імпульсної лазерної дії. При різних інтенсивностях опромінення може відбуватись або процес нагріву поверхні, або плавлення, або випаровування.

Під час дії лазерного випромінювання з енергією кванта на напівпровідник відбувається поглинання в тонкому поверхневому шарі товщиною см (α – коефіцієнт оптичного поглинання).

Під час взаємодії світлового імпульсу з напівпровідником відбуваються процеси:

1. утворення електронно діркових пар

2. дифузія надлишкових носіїв заряду з області генерації

3. термалізація гарячих електронів і дірок до квазіврівноважного стану з відповідним заселенням рівнів

4. рекомбінація носіїв і передача гратці енергії рекомбінації

5. дифузійно-просторовий перерозподіл теплової енергії гратки, яка виділяється при термалізації і рекомбінації носіїв.

(Тобто, спочатку створюється сильна відмінність між електронною температурою і температурою гратки. Процес передачі і термалізації енергії в гратці включає в себе як релаксацію всередині електронно-діркової підсистеми, так і електронно-фононну і фонон-фононну релаксацію).

Домінуючим ефектом при імпульсному лазерному відпалі є неоднорідна (із значним градієнтом температури) за об’ємом і за часом нагрівання кристалу. Важливими є розподіл температури в твердому тілі та еволюція температури на поверхні. Розрахунок температури профілів в напівпровіднику є дещо ускладнений в порівнянні з металами.

Процес нагріву описується одномірним рівнянням теплопровідності:

, де C – теплоємність, К – коефіцієнт теплопровідності, – густина, – коефіцієнт полинання, Q – тепловідведення у зовнішнє середовище, питома напруженість лазерного випромінювання в середині зразка, R коефіцієнт відбивання. P(t)

для П-імпульсів, P(t)= ;

У загальному випадку рівняння нелінійне і має розв’язок чисельними методами.

Розподіл температур за глибиною має монотонно-спадний характер.

На поверхні Т швидко зростає (майже лінійно), досягаючи максимального значення в момент закінчення імпульсу і повільніше спадає.

Фізичні основи іонної імплантації

Відповідно до класичної теорії Ліндхарда, Шарффа і Шіотта (ЛШШ) профілі імплантованих домішок описують гаусівським розподілом:

; – помилка до 1 %.

Проте реальні профілі асиметричні (це помітно для легких іонів при незначних дозах імплантації).

Точніший вираз: ,

Який враховує, що іони гальмують в об’ємі напівпровідника, який займає простір

від 0 до +∞ (а не від -∞ до +∞).

Для асиметричних профілів апроксимують двома спряженими половинами гаусівських розподілів з пробігом і розкидом пробігів ∆ і ∆ . Концетр. профіль легуючої домішки:

;

;

Розподіл іонів бору в Si найкраще описує розподіл Пірсона, який в загальному вигляді визначний діфрівнянням:

, де

∙ arctg ) , де

К визначають з умови нормування

Функція розподілу Пірсона центрована в точці – середнього нормального пробігу.

Важливість точного розрахунку профілю імплантованих домішок необхідна для розрахунку подальшої дифузійної розгонки.

Фізичні основи дифузії. Дифузія у виродженому напівпровіднику.

Швидкість накопичення домішки визначає другий закон Фіка:

, де

Для випадку високих значень концентрації С домішки в напівпровіднику, коефіцієнт дифузії залежить від концентрації 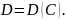У вироджених напівпровідниках при

( густина станів у C,V-зонах):

, тоді необхідно врахувати в розв’язку рівняння Фіка

У результаті розгонка домішки буде відбуватись швидше

Дифузія імплантованої домішки при імпульсному відпалі:

Домінуючий ефект при імп. лазерному відпалі є неоднорідним за об’ємом і часом нагріву кристалу. Дифузійні процеси проходять в умовах великих температурних градієнтів та термопружних полів. Виникають потоки фононів, які захоплюють атоми домішки. Тоді на атом домішки діє сила:

, елементарний об’єм атома напівпровідника, атома домішки, усереднене відношення перерізів розсіяння фононів атомами напівпровідника та домішки, оператор Пуасона.

Поле пружних деформацій діє на домішку з силою: ,

де n – коефіцієнт Пуасона, модуль зсуву, вектор поля зміщення, оператор Лапласа.

, коефіцієнт температурного розширення.

Тоді вираз швидкості руху домішкового атома:

, домішковий потік ,

а другий закон Фіка:

Це рівняння необхідно розв’язувати з рівнянням теплопровідності.

Залежно від напряму термопружних сил процес дифузії може прискорюватись або сповільнюватись.