29 Розв’язком рівняння ( ), який задовольняє умовам , є функція:
а)
;
Рівняння вільних коливань струни, закріпленої на кінцях:
має рішення виду
,
де коефіцієнти Аn і Вn знаходять із початкових умов:
, ;
30
Розв’язком рівняння
(
),
якийзадовольняє умовам
,
є функція: в)
;
Рівняння вільних коливань струни, закріпленої на кінцях:
має рішення виду
,
де коефіцієнти Аn і Вn знаходять із початкових умов:
, ;
31
Розв’язком
рівняння
(
),
який задовольняє умовам
,
є функція: г)
;
Рівняння виду с крайовими умовами
і початковою умовою
описує закон розподілу температури в однорідному стрижні довжини l, на кінцях якого підтримується нульова температура. Функція F(x;t) характеризує існуючі усередині стрижня точки (джерела) виділення або поглинання тепла. Якщо такі відсутні, F(x;t)=0 і рівняння називається однорідним.
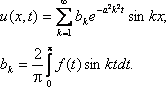
Отримуємо: 
,
32
Розв’язком рівняння
(
),
який задовольняє умовам
,
є функція: б)
;
Рівняння виду с крайовими умовами
і початковою умовою
описує закон розподілу температури в однорідному стрижні довжини l, на кінцях якого підтримується нульова температура. Функція F(x;t) характеризує існуючі усередині стрижня точки (джерела) виділення або поглинання тепла. Якщо такі відсутні, F(x;t)=0 і рівняння називається однорідним.
Отримуємо: 
,
33 Розв’язком рівняння ( ), який задовольняє умовам , є функція:
а)
;
Рівняння виду
с
крайовими умовами
і
початковою умовою
описує закон розподілу температури в однорідному стрижні довжини l, на кінцях якого підтримується нульова температура. Функція F(x;t) характеризує існуючі усередині стрижня точки (джерела) виділення або поглинання тепла. Якщо такі відсутні, F(x;t)=0 і рівняння називається однорідним.
Отримуємо: ,
32 Розв’язком рівняння ( ), який задовольняє умовам , є функція: б) ;
Рівняння виду с крайовими умовами
і початковою умовою
описує закон розподілу температури в однорідному стрижні довжини l, на кінцях якого підтримується нульова температура. Функція F(x;t) характеризує існуючі усередині стрижня точки (джерела) виділення або поглинання тепла. Якщо такі відсутні, F(x;t)=0 і рівняння називається однорідним.
Отримуємо: 
,
34 Розв’язком рівняння ( ),який задовольняє умовам , є функція:
в)
;
Рівняння виду
с крайовими умовами і початковою умовою
описує закон розподілу температури в однорідному стрижні довжини l, на кінцях якого підтримується нульова температура. Функція F(x;t) характеризує існуючі усередині стрижня точки (джерела) виділення або поглинання тепла. Якщо такі відсутні, F(x;t)=0 і рівняння називається однорідним.
Отримуємо:
,
