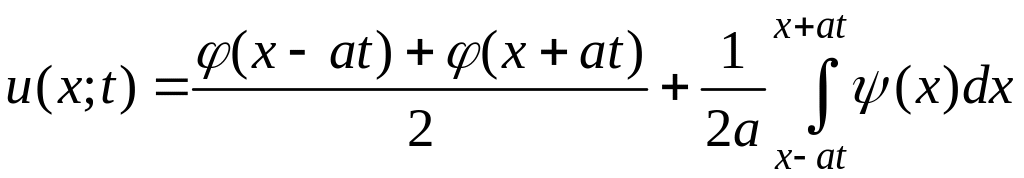ВИЩА МАТЕМАТИКА
розділ 8
рівень B
1 Вказати загальний розв’язок рівняння ( - довільні функції).
а)
;
2
Вказати загальний розв’язок
рівняння
(
- довільні функції).
в)
;
3
Вказати загальний розв’язок
рівняння
(
- довільні функції).
б)
;
4
Вказати загальний розв’язок
рівняння
(
- довільні функції).
г)
;
5
Вказати загальний розв’язок рівняння
(
- довільні функції).
б)
;
6
Вказати загальний розв’язок
рівняння
(
- довільні функції).
в)
;
;
д) інша відповідь.
7
Вказати загальний розв’язок рівняння
(
- довільні функції).
а)
;
8
Вказати загальний розв’язок
рівняння
(
- довільні функції).
г)
;
9
Вказати загальний розв’язок
рівняння
(
-
довільні функції).
б)
;
10Вказати
загальний розв’язок рівняння
(
- довільні функції).
в)
;
11
Рівняння вільних коливань струни має
вид: б)
;
Якщо
щільність
стала,
,
то рівняння коливань струни приймає
вигляд:
,
де
- сталі.
12
Рівняння теплопровідності в стержні
має вид: г)
;
Рівня́ння теплопові́дності — рівняння, що визначає закон зміни температури з часом при теплопередачі через теплопровідність.
де c — питома теплоємність, q — тепловий потік, S — джерело тепла.
У
випадку, коли тепловий потік пропорційний
градієнту температури (закон Фур'є)
,
закон теплопровідності набирає форми:
Це неоднорідне диференційне рівняння в часткових похідних параболічного типу, схоже на рівняння дифузії.
Здебільшого при розв'язуванні рівняння теплопровідності вважають, що теплоємність і коефіцієнт теплопровідності не залежать від температури. В такому випадку рівняння теплопровідності стає лінійним.
13
Рівняння Лапласа має вид: в)
;
Рівняння
Лапласа — однорідне лінійне рівняння
в часткових похідних другого порядку
еліптичного типу.
Функції, які задовільняють рівнянню Лапласа, називаються гармонічними.
14
Розв’язок задачі про вільні коливання
струни, закріпленої на кінцях
має вид:
а)
;
Рівняння виду
(1)
с крайовими умовами
(2)
і початковими умовами
(3)
(4)
описує закон коливань однорідної тонкої нерозтяжної струни довжини l, закріпленої на кінцях у точках х=0 і х=l (умови (2)), з початковою формою (х) (умова (3)) і початковою швидкістю (х) (умова (4)), у поле дії зовнішньої сили (наприклад, сили ваги, у магнітному полі й т.п.). Постійний параметр a2 залежить від властивостей струни, функція F(x;t) - від зовнішньої сили. Якщо F(x;t)=0 – це значить, що зовнішньої сили немає (або їй можна зневажити) і коливання називаються вільними.
Відзначимо, що коливання розглядаються малі (відхилення u крапок струни від положення рівноваги – осі Ох – мало), плоскі (коливання відбуваються тільки в площині хOu), поперечні (кожна крапка струни рухається строго перпендикулярно положенню рівноваги).
Рівняння вільних коливань струни, закріпленої на кінцях:
має рішення виду
,
де коефіцієнти Аn і Вn знаходять із початкових умов:
Тобто,
оскільки
,
то
=0,
тому складова Bn=0/
15
Розв’язок
задачі про вільні коливання струни,
закріпленої на кінцях
має вид:
б)
;
Рівняння виду
(1)
с крайовими умовами
(2)
і початковими умовами
(3)
(4)
описує закон коливань однорідної тонкої нерозтяжної струни довжини l, закріпленої на кінцях у крапках х=0 і х=l (умови (2)), з початковою формою (х) (умова (3)) і початковою швидкістю (х) (умова (4)), у поле дії зовнішньої сили (наприклад, сили ваги, у магнітному полі й т.п.). Постійний параметр a2 залежить від властивостей струни, функція F(x;t) - від зовнішньої сили. Якщо F(x;t)=0 – це значить, що зовнішньої сили немає (або їй можна зневажити) і коливання називаються вільними.
Відзначимо, що коливання розглядаються малі (відхилення u крапок струни від положення рівноваги – осі Ох – мало), плоскі (коливання відбуваються тільки в площині хOu), поперечні (кожна крапка струни рухається строго перпендикулярно положенню рівноваги).
Рівняння вільних коливань струни, закріпленої на кінцях:
має рішення виду
,
де коефіцієнти Аn і Вn знаходять із початкових умов:
підставляючи t=0 одержуємо
=0
pf evjdj.
тобто Аn – коефіцієнти Фур'є для функції (х) при розкладанні на інтервалі (0; l) по синусах кратних дуг.
Далі, диференціюючи u(х;t) по t і підставляючи t=0 одержуємо:
,
тобто
–
коефіцієнти Фур'є для функції (х)
при розкладанні на інтервалі (0; l)
по синусах кратних дуг.
Отже, складова An=0, тому розв’язок має вид:
16
Розв’язок задачі про вільні коливання
струни, закріпленої на кінцях
має вид:
в)
,
;
Рівняння виду
(1)
с крайовими умовами
(2)
і початковими умовами
(3)
(4)
описує закон коливань однорідної тонкої нерозтяжної струни довжини l, закріпленої на кінцях у крапках х=0 і х=l (умови (2)), з початковою формою (х) (умова (3)) і початковою швидкістю (х) (умова (4)), у поле дії зовнішньої сили (наприклад, сили ваги, у магнітному полі й т.п.). Постійний параметр a2 залежить від властивостей струни, функція F(x;t) - від зовнішньої сили. Якщо F(x;t)=0 – це значить, що зовнішньої сили немає (або їй можна зневажити) і коливання називаються вільними.
Відзначимо, що коливання розглядаються малі (відхилення u крапок струни від положення рівноваги – осі Ох – мало), плоскі (коливання відбуваються тільки в площині хOu), поперечні (кожна крапка струни рухається строго перпендикулярно положенню рівноваги).
Рівняння вільних коливань струни, закріпленої на кінцях:
має рішення виду
,
де коефіцієнти Аn і Вn знаходять із початкових умов: підставляючи t=0 одержуємо ,
тобто Аn – коефіцієнти Фур'є для функції (х) при розкладанні на інтервалі (0; l) по синусах кратних дуг.
Далі, диференціюючи u(х;t) по t і підставляючи t=0 одержуємо:
,
тобто – коефіцієнти Фур'є для функції (х) при розкладанні на інтервалі (0; l) по синусах кратних дуг.
, ;
17
Розв’язок задачі про вільні коливання
нескінченної струни
має вид: г)
;
Рівняння вільних коливань нескінченної струни:
(без крайових умов)
вирішують за допомогою формули Даламбера:
