5. Кинетика

Кинетика объединяет статику и геометрию масс.

5.1. Кинетический торсор.

Материальная система S движется относительно системы координат R0.

Два векторных поля

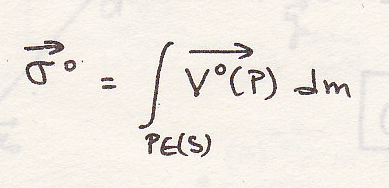
-количество движения системы

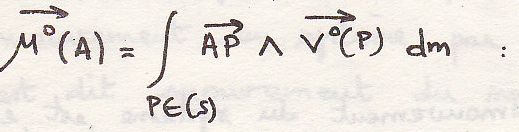
-кинетический момент системы в точке А

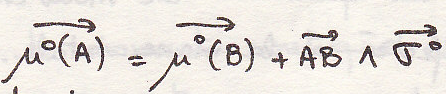
(A и B – точки системы)

Это торсор кинетический или количество движения

5.1.2 Расчет кинетической суммы.

По определению

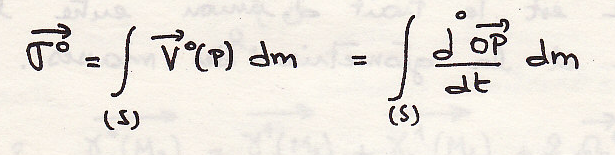
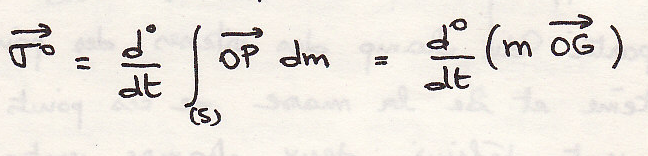
В галилеевской механике масса инвариантна:

-центр инерции системы

И так

Количество движения системы равно количеству движения центра инерции, отнесенной ко всей массе системы

5.2. Теорема Кёнига.

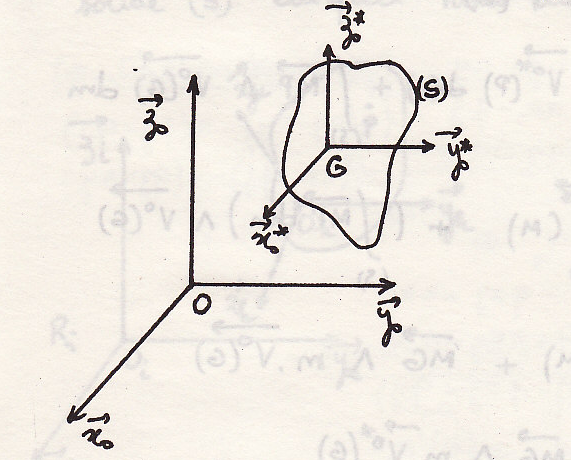
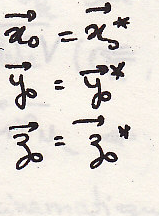
Материальная система (S) движется относительно неподвижной СИ ( ).Введем СИ Кёнига, ( ) центр которой совпадает с центром тяжести (S) и которая совершает поступательное движение относительно .

Движение системы по отношению к системе называется движение системы вокруг центра инерции. Мы соединим кинетический момент системы в его движении по отношению к системе и кинетический момент в движении вокруг центра инерции.

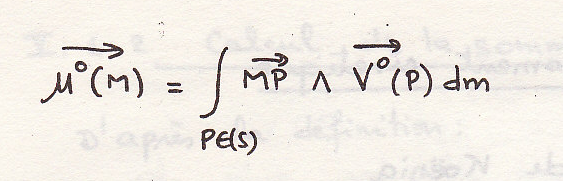
После сложения скоростей

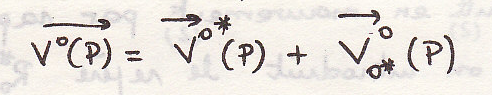
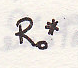при переходе к

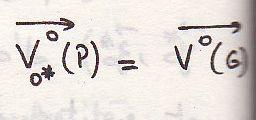
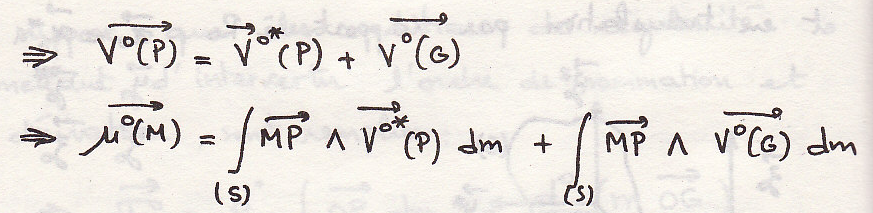
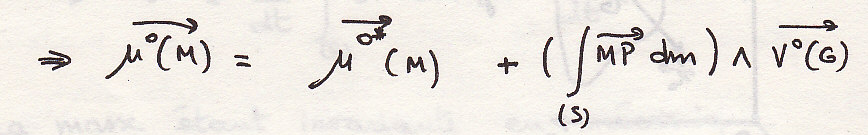
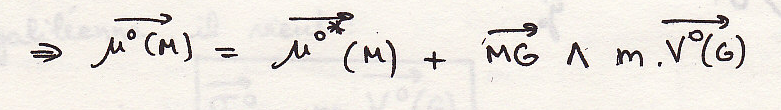
Или

Так как -начало координат

Следовательно

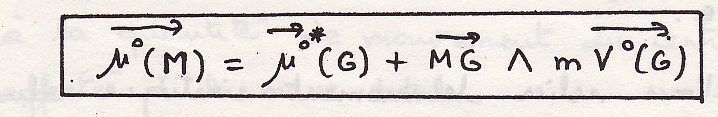
Теорема Кенига для кинетического момента

Кинетическая энергия материальной системы в ее абсолютном движении складывается из кинетической энергии центра масс, в предположении, что в нем сосредоточена масс всей системы, и кинетической энергии системы в ее движении относительно поступательно перемещающихся в инерциальном пространстве вместе с центром масс осей.

Кинетический момент системы в его движении по потношению к равен кинетическому моменту при движении вокруг центра инерции, увеличенный на кинетический момент центра инерции, отнесённый к всей массе.

b. Кинетический момент в точке твердого тела

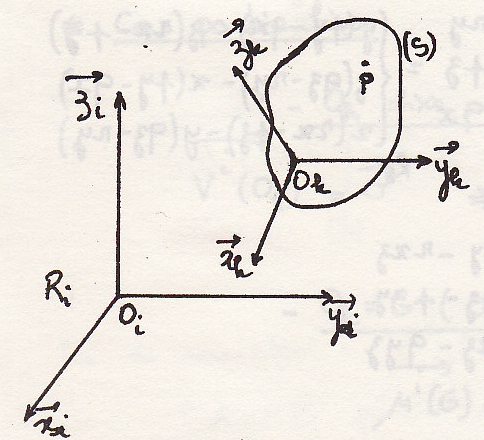
Посчитаем кинетический момент в точке твердого тела

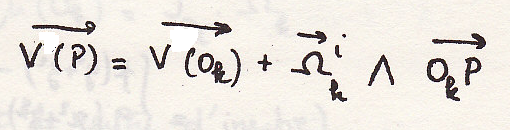
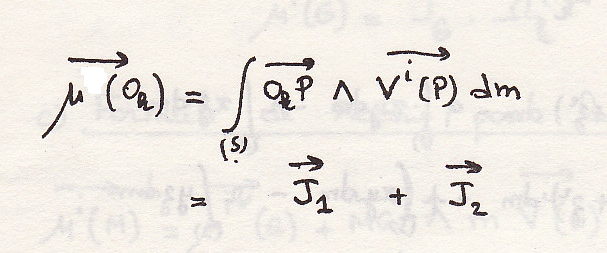
пропущено

Посчитаем последний интеграл:

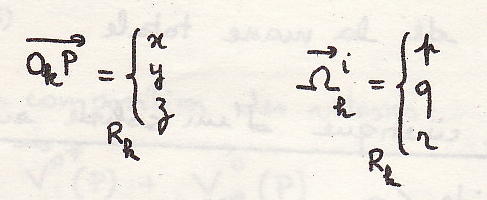
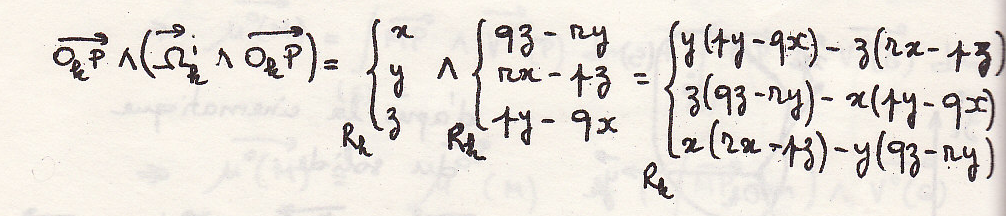
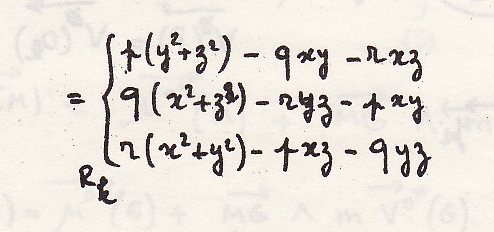
Откуда

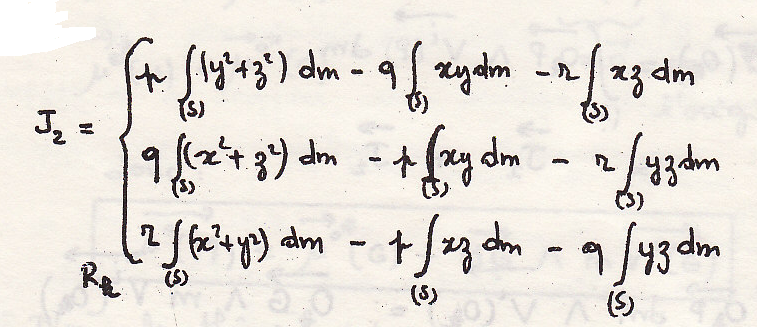
Наконец

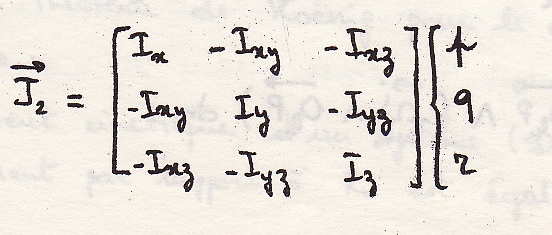
пропушено

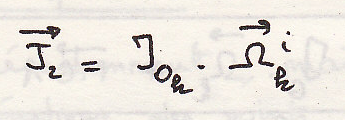
В итоге

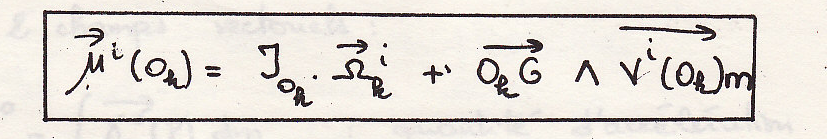
Частные случаи.

1. фиксирована в системе

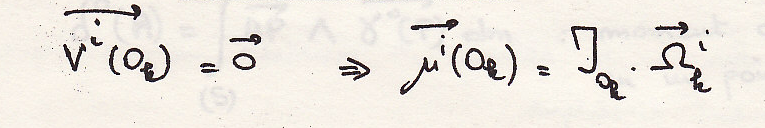
2.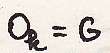 , -центр инерции

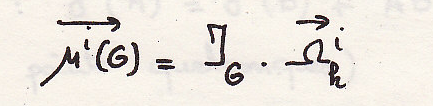
С. Формула Кёнига для твердого тела

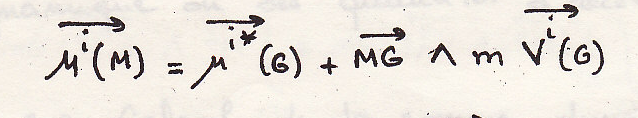
Или

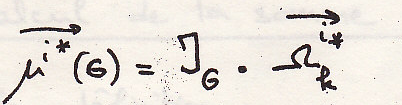
Откуда следует фундаментальная и очень важная формула для твердого тела

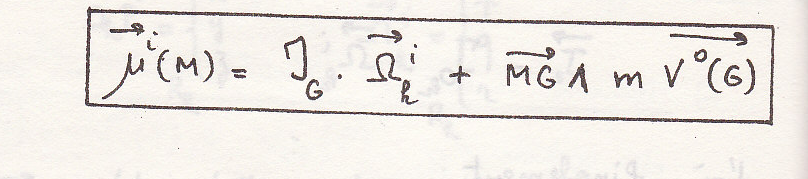
5.2 Динамический торсор

Определение

Как и ранее можно выразить два векторных поля:

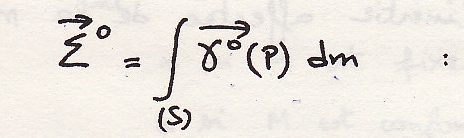
количество ускорения системы

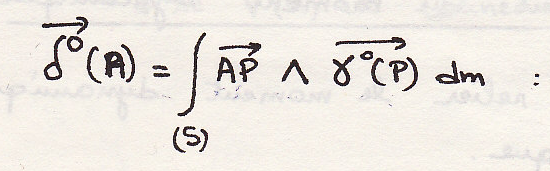
динамический момент в точке А

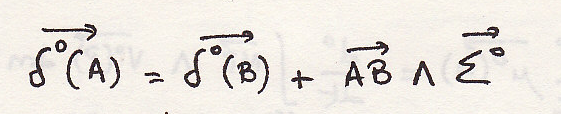
Это динамический торсор или количества ускорения.

5.2.2. Расчет динамической суммы

По определению

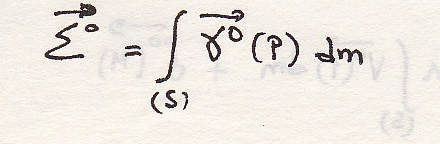
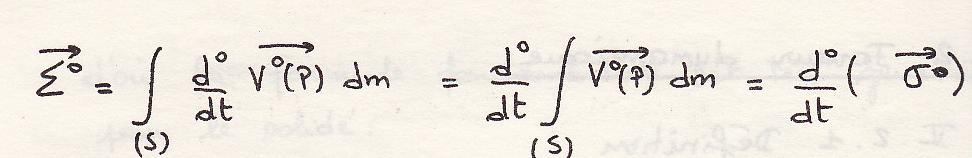
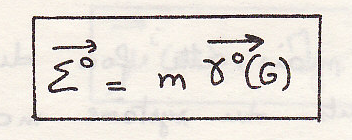
Стало быть количество ускорения системы равно количеству ускорения центра инерции, отнесенного ко всей массе.

5.2.2. Расчет динамического момента

Мы хотим связать динамический и кинетический момент

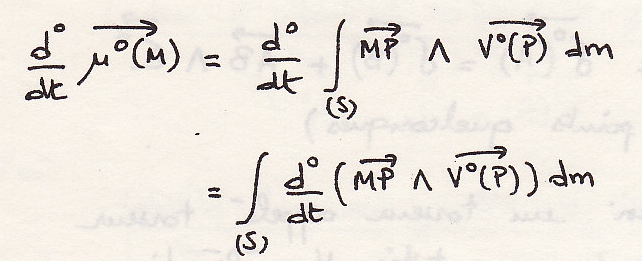
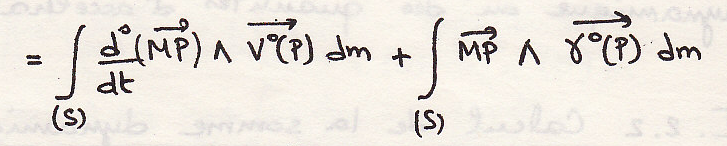
Или

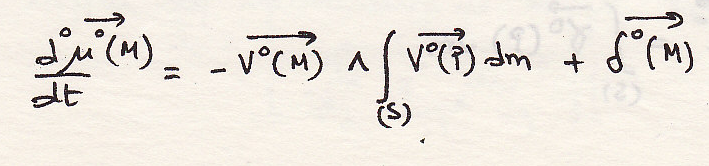откуда

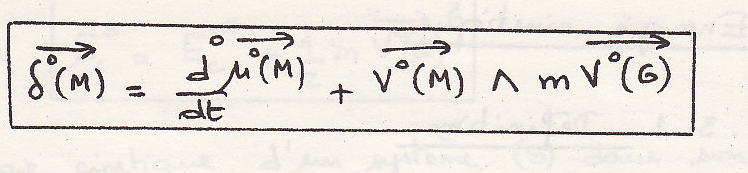
- в этой формуле точка М – геометрическая точка

-

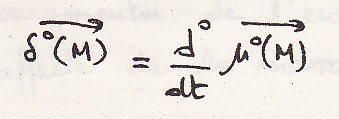
в трех частных случаях:

1. если точка М зафиксирована в

2. если точка М совмещена с центром инерции G

3. если 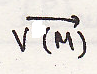коллинеарен с

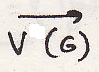
5.3 Кинетическая энергия

5.3.1 Определение

Если материальная система движется по отношению к , по определению её кинетическая энергия – скалярная величина:

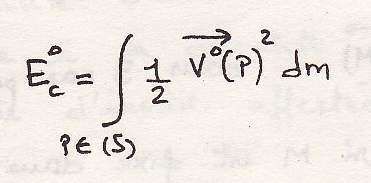
5.3.2 Расчет кинетической энергии:

Как и ранее принимается во внимание система Кенига ,

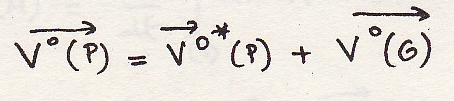
Откуда

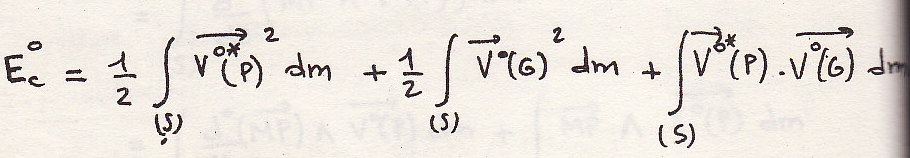
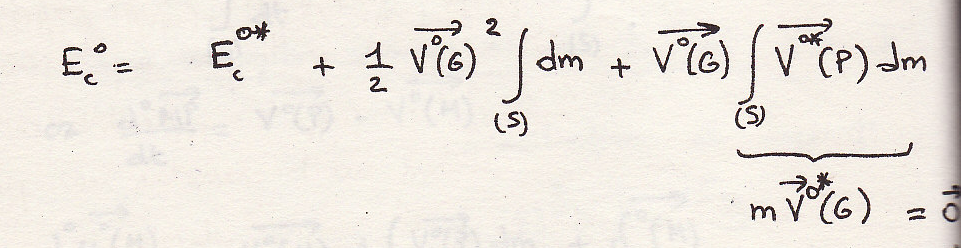
Так как G – начало координат

Следовательно

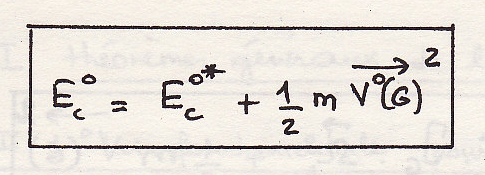
Кинетическая энергия системы в ее движении по отношению к равна кинетической энергии при движении вокруг центра инерции, увеличенной на кинетическую энергию центра инерции, отнесённой к всей массе.

- Случай твердого тела

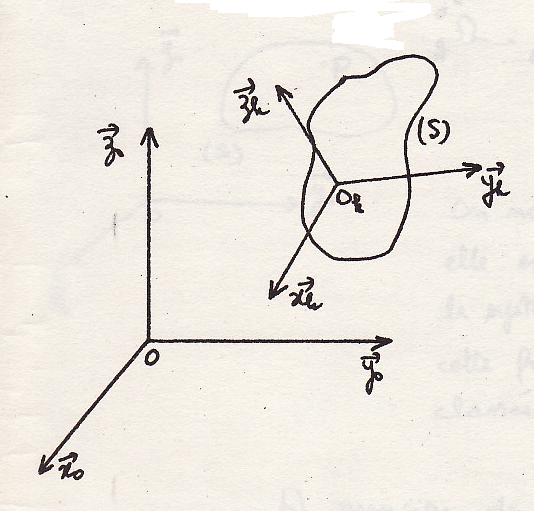
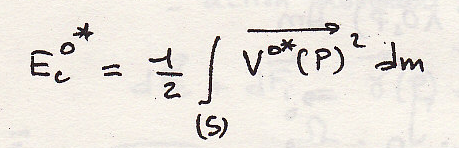
Или

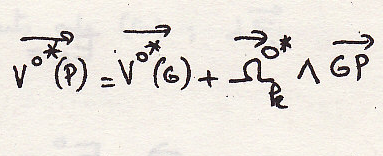
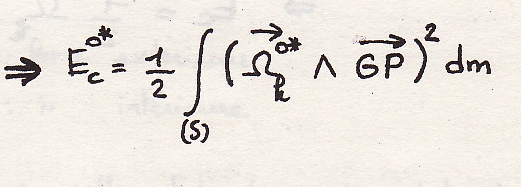
Предполагаем, что расчет идем в геометрии масс:

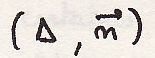
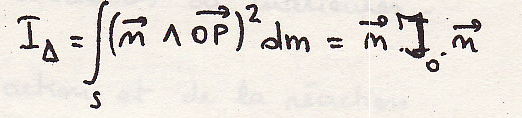
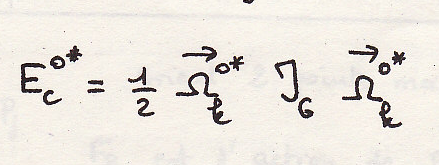
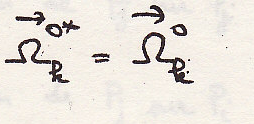
Откуда

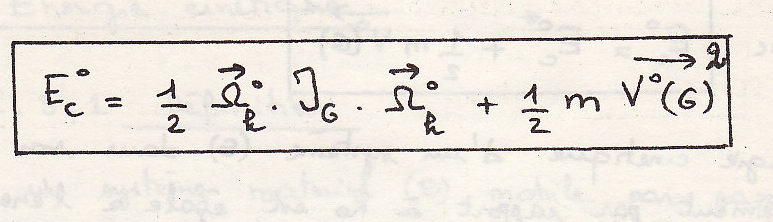
• Располагаем фиксированной точкой 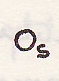в системе :

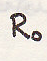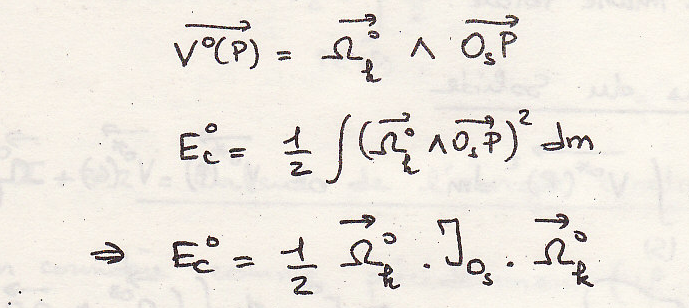
6. Общие теоремы динамики

6.1 Фундаментальный закон для материальной системы

a) Форма фундаментального закона

Имеем материальную точку P, принадлежащую материально системе . На Р действуют две категории сил:

- внешние силы

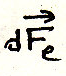
-внутренние силы

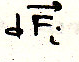
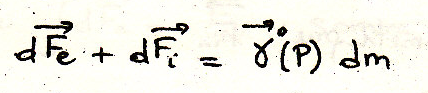
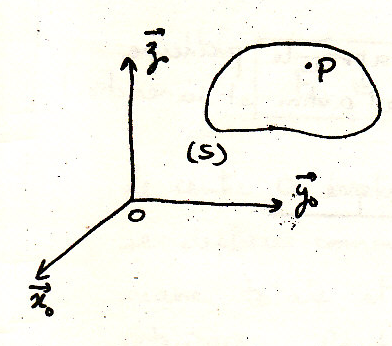
Тут пропущено

b) Принцип действия и противодействия

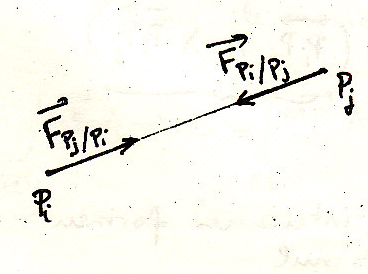
Имеются 2 материальные точк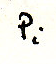и и

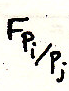- действие на

- действие на

Принцип действия и противодействия выразится в форме

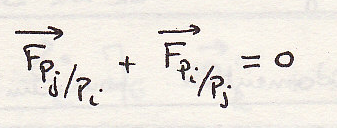
Это означает

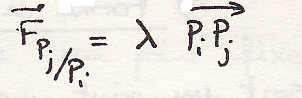
С) Свойства внутренних сил

Посчитаем элементы торсора внутренних сил

-Геометрическая сумма

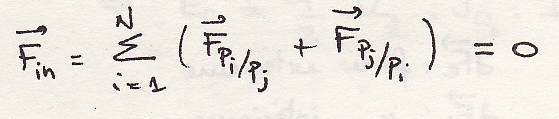
-Момент в точке О

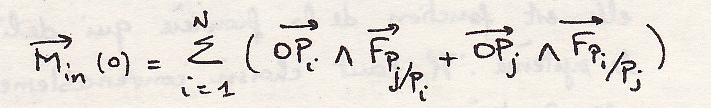
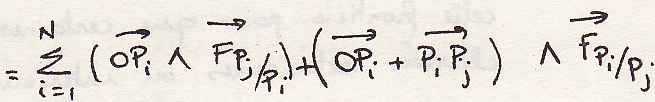
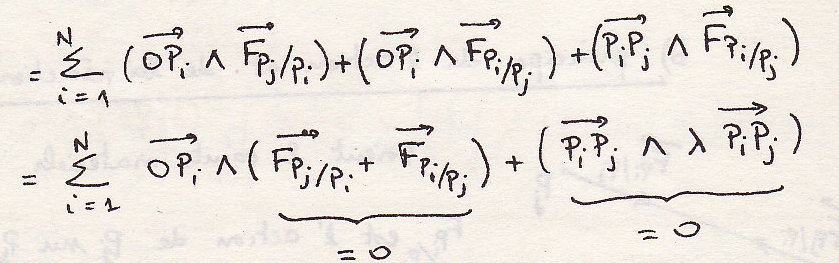
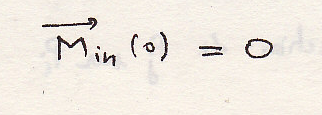
Внутренние силы образуют нулевой торсор.

6.2. Теорема о кинетической результирующей

Система 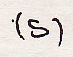состоит из множества материальных точек:

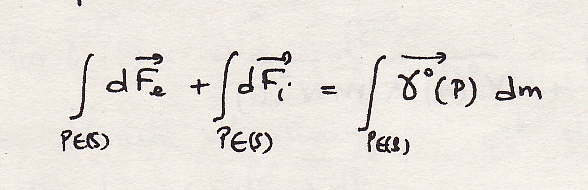
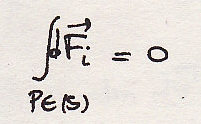
Внутренние силы образуют нулевой торсор.

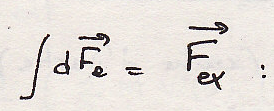
сумма внешних сил

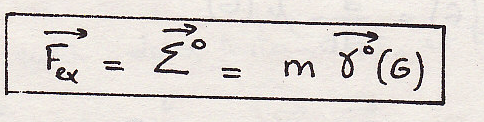
Центр инерции какой бы ни было материальной системы перемещается как материальная точка, отнесенная ко всей массе и на которую воздействуют сумма внешних сил. Эта теорема исключает воздействие материальной точки.

6.3. Теорема о кинетическом моменте

Пусть момент в точке М:

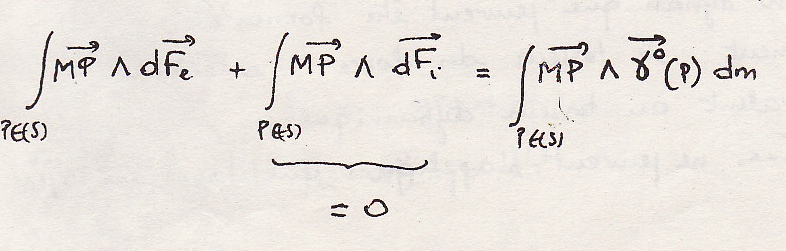
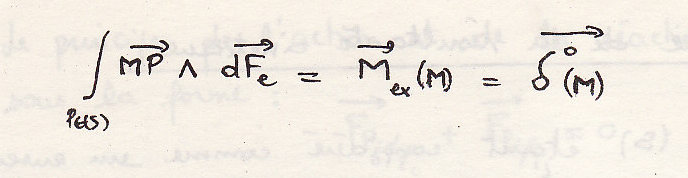
И так как

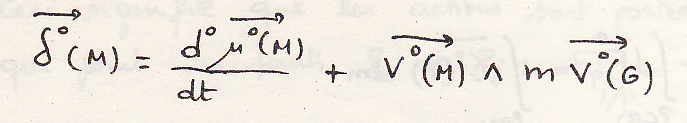
И так

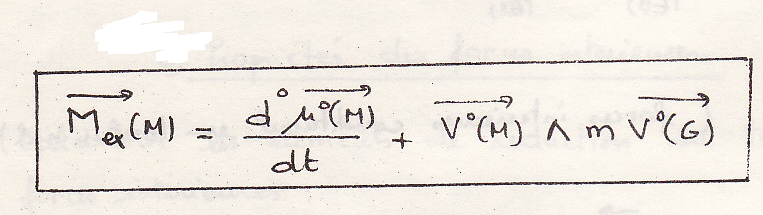
-1 случай если 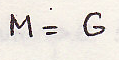(центр инерции)

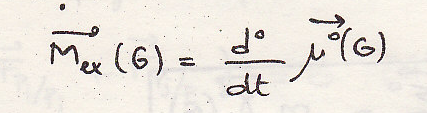
-2 случай если зафиксирована в

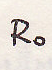
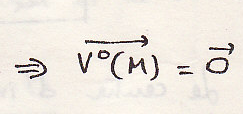
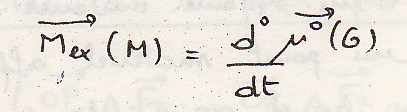
Момент внешних сил в точке равен динамическому моменту в этой точке

Поправки:

-Теорема о геометрической сумме и теорема о динамическом моменте могут быть сформулированы совместно: торсор внешних сил эквивалентен динамическому торсору

-эти теоремы могут быть использованы только в галилеевской системе координат

6.4 Теорема о кинетической энергии

В соседстве с земной поверхностью, в галилеевской системе координат, для каждой точки Р имеем:

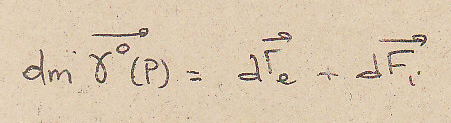
Силы инерции приведения в движение и Кориолисовы силы ничтожны по сравнению с :

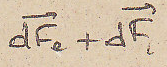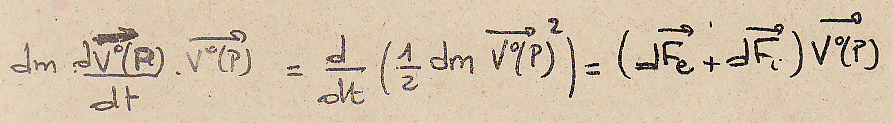
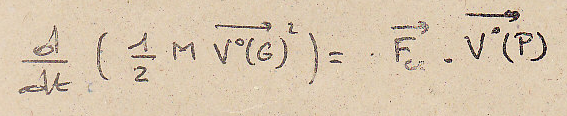
Проинтегрируем по двум параметрам t1 и t2:

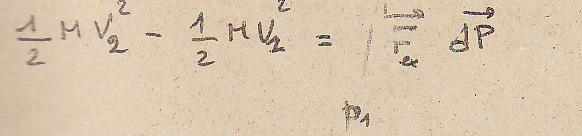
Работа силы на перемещении

Откуда

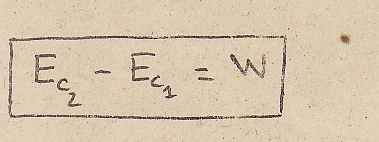
Случай, когда сила 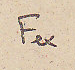производная от функции потенцильной энергии:

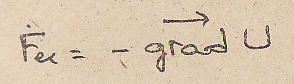
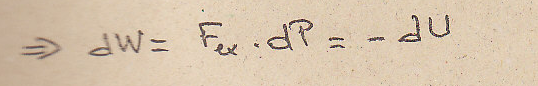
Применяя теорему кинетической энергии в дифференциальной форме

Литература

Ивченко В.А. Техническая механика. М. ИФРРА-М 2003

Олофинская В.П. Техническая механика. М. Форум 2005

Савельев И.В. Курс общей физики. Механика. М. Астрель 2004

Тарг С.М. Краткий курс теоретической механики. М. Высшая школа 1995.