Плоская система произвольно расположенных сил и условие ее равновесия

П

риведение силы к данной точке заключается в том,

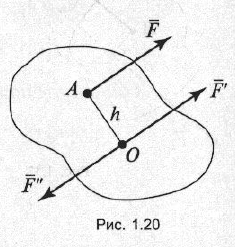
что рассматриваемую силу F переносят параллельно

самой себе в произвольно выбранную точку О. Для

того чтобы механическое состояние тела не измени­лось,

силу F' уравновешивают силой F" (рис. 1.20). В

результате приведения силы F к точке О получи­лась

система сил, состоящая из силы F', равной и параллельной

данной силе F, и пары сил (F и F"), момент которой равен

моменту данной силы F от­носительно точки О:

М = M₀(F).

Плоской системой произвольно расположенных сил называется система сил, линии действия которых лежат в одной плоскости, но не пересекаются в одной точке (рис. 1.21).

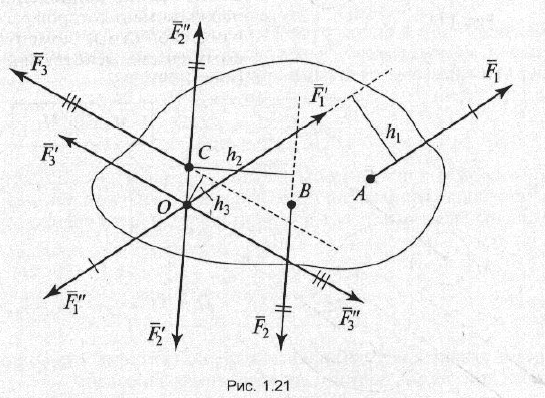
Для того чтобы привести данную систему произвольно расположенных сил к произвольно выбранной точке О(см.рис. 1.21), необходимо:

1)перенести по очереди каждую силу в эту точку;

2)уравновесить силы ( ) силами ( ).

В результате приведения сил (F₁,F₂,F3) к точке О получили новую сис­тему сил, состоящую из плоской системы сходящихся сил ( ), кото­рые равны и параллельны данным силам, т.е.

(1.1)

Эту вновь полученную систему сходящихся сил (1.1) заменяем равнодей­ствующей силой, которая равна геометрической сумме данных сил и назы­вается главным вектором системы:

В результате приведения получили еще одну систему пар сил

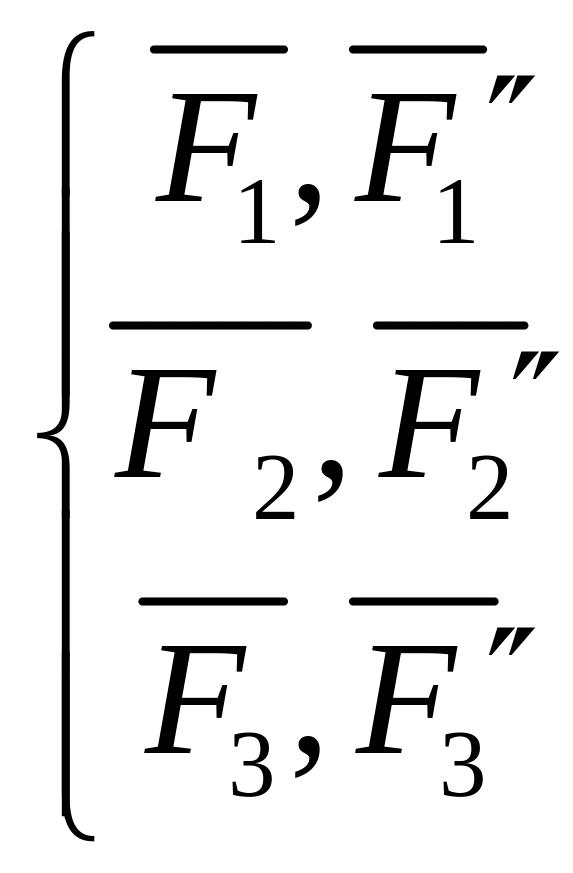
моменты которых равны моментам данных сил относительно точки О, т.е.

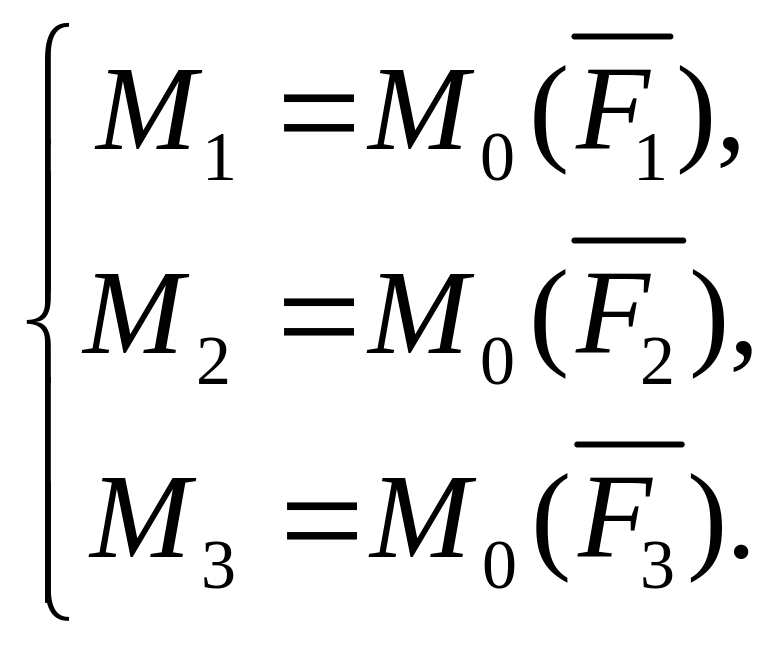
Вновь полученную систему пар сил (1.2) заменим одной равнодейству­ющей парой, момент которой равен алгебраической сумме моментов слага­емых пар сил и называется главным моментом системы:

Таким образом, для того чтобы тело под действием плоской системы про­извольно расположенных сил находилось в равновесии, необходимо, чтобы главный вектор и главный момент системы были равны нулю:

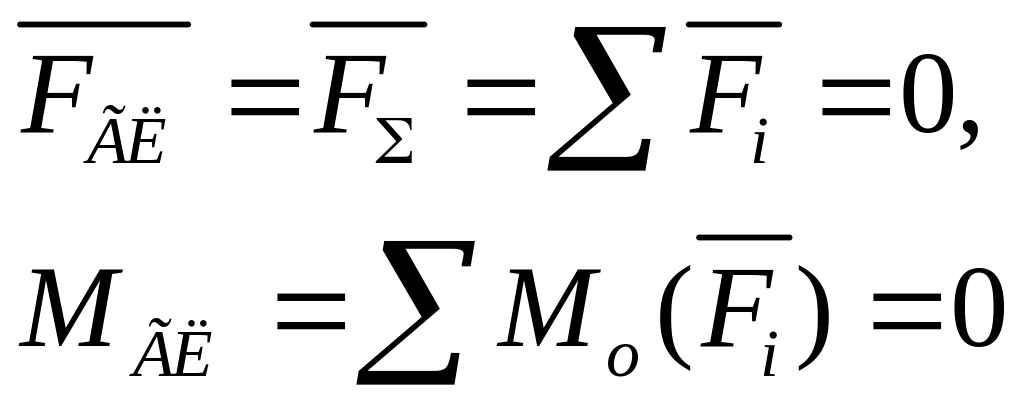
Выразив главный вектор вновь полученной системы сходящихся сил в аналитической форме, получим два уравнения равновесия:

Главный момент системы заменим алгебраической суммой моментов дан­ных сил относительно точки приведения:

Таким образом, получаем условие равновесия плоской системы произвольно расположенных сил: алгебраическая сумма проекций всех сил на оси х и у должна быть равна нулю и алгебраическая сумма моментов всех сил относи­тельно точки приведения должна быть равна нулю, т.е.

- первая (основная)

форма уравнения равновесия;

- вторая форма;

- третья форма.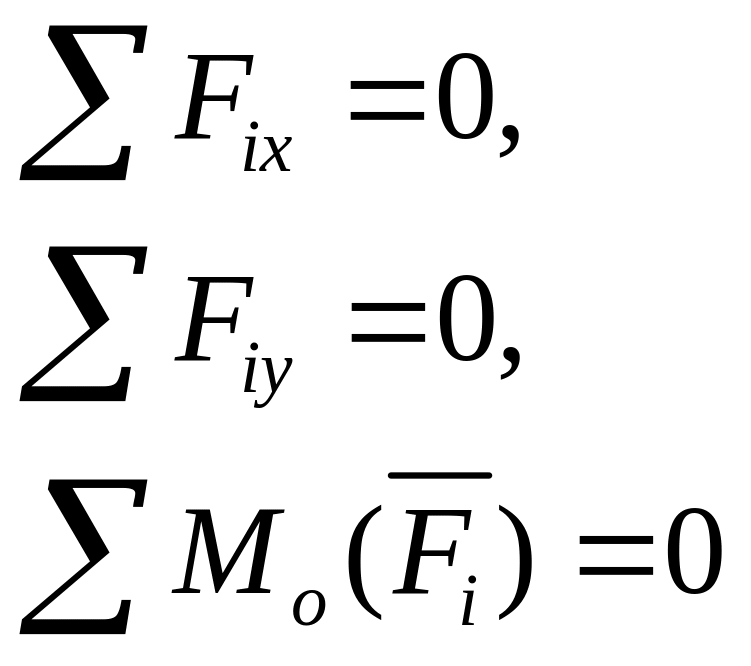

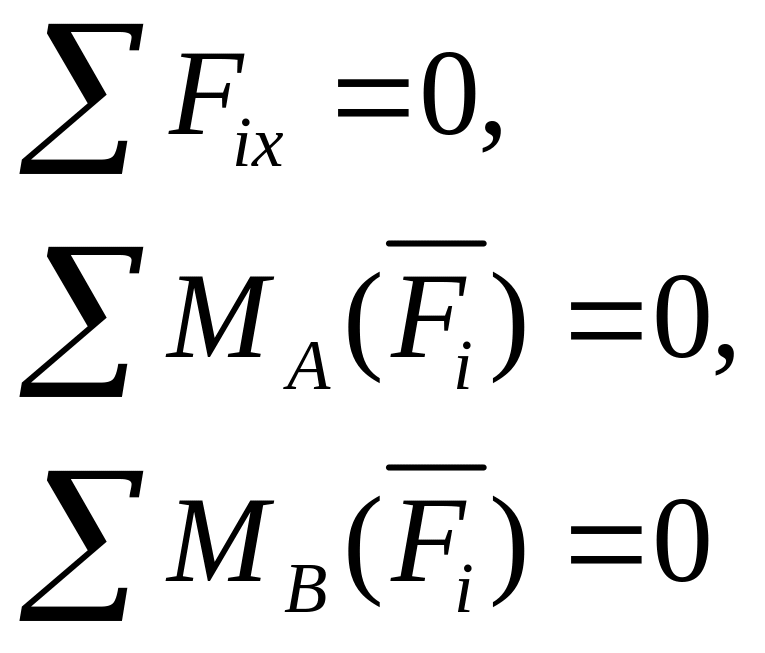
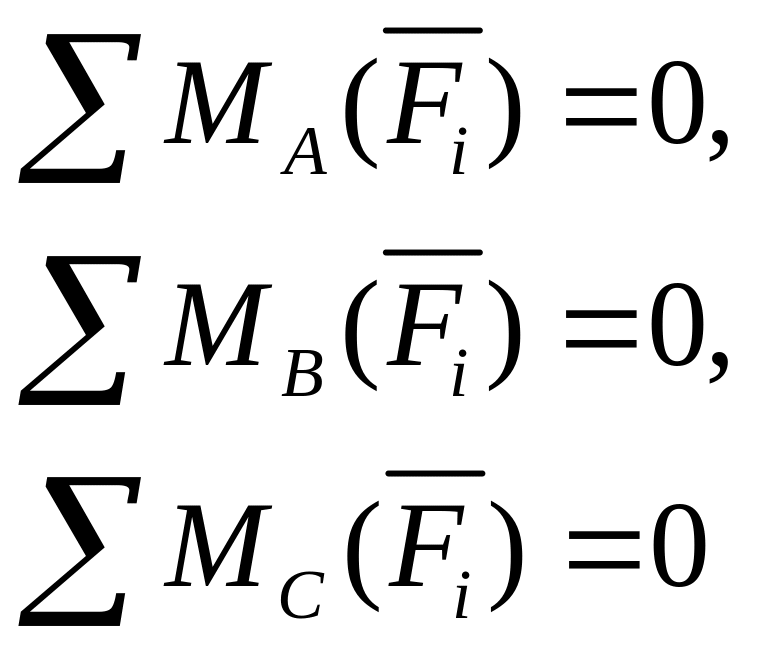
Пространственная система сил

П

ространственной системой сходящихся сил называется система сил, линии действия которых не лежат в одной плоскости, но пе­ресекаются в одной точке. Равнодейству­ющая такой системы сил изображается диагональю прямоугольного параллелепипеда построенного на этих силах как на сторонах (рис. 1.22).

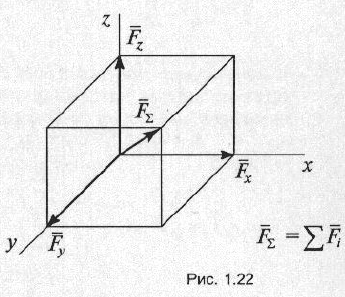
Условие равновесия пространственной си­стемы сходящихся сил: алгебраическая сум­ма проекций всех сил на три взаимно перпендикулярные оси координат должны быть равны нулю, т.е.

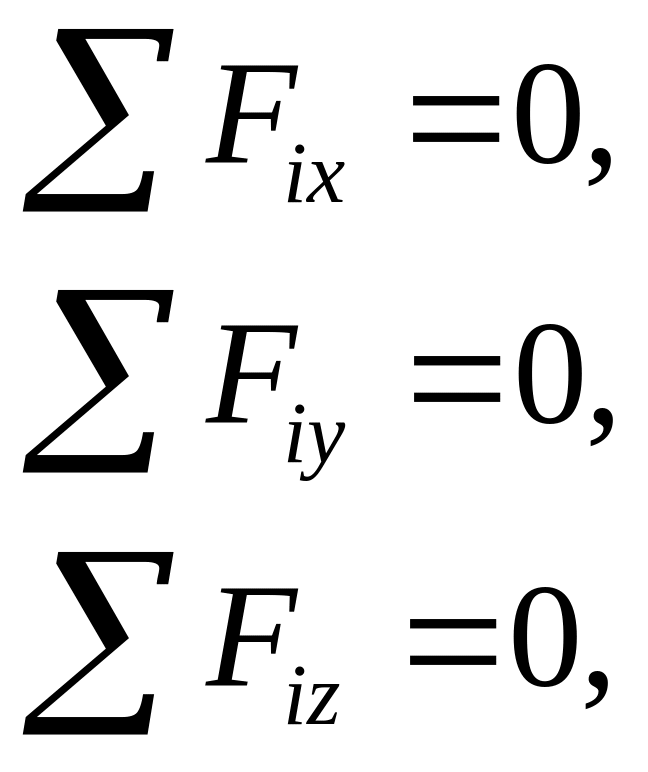
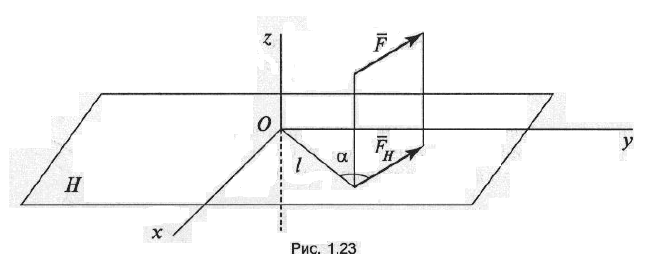
Для того чтобы найти монет силы F относительно оси z, надо спроектировать силу F на плоскость H, перпендикулярную оси z (рис. 1.23), затем найти момент проекции F_H относительно точки О, которая является точкой пересечения плоскости H с осью z. Момент проекции F_H и будет являться мо­ментом силы F относительно оси z:

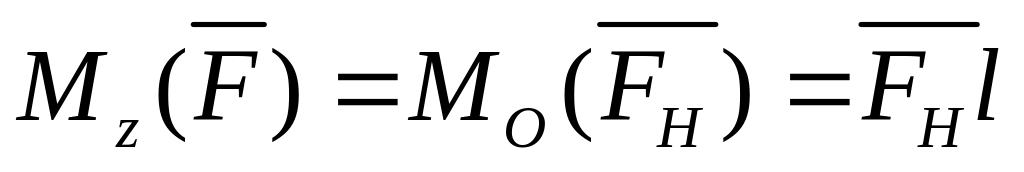
Моменты сил, перпендикулярных и параллельных оси z, будут равны нулю (рис. 1.24).

П

ространственной системой произвольно распложенных сил называется система сил, линии действия которых не лежат в одной плоскости и не пересекаются в одной точке. Равнодействующая такой системы сил также равна геометрической сумме этих сил, но изображается диагональю сложных объемных фигур (тетраэдр, октаэдр и т.д.).

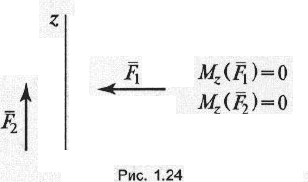
Условие равновесия пространственной системы произвольно расположенных сил: алгебра­ическая сумма проекций всех сил на три взаимно перпендикулярные оси ко­ординат должна быть равна нулю и алгебраическая сумма моментов всех сил относительно тех же осей координат должна быть равна нулю, т.е.

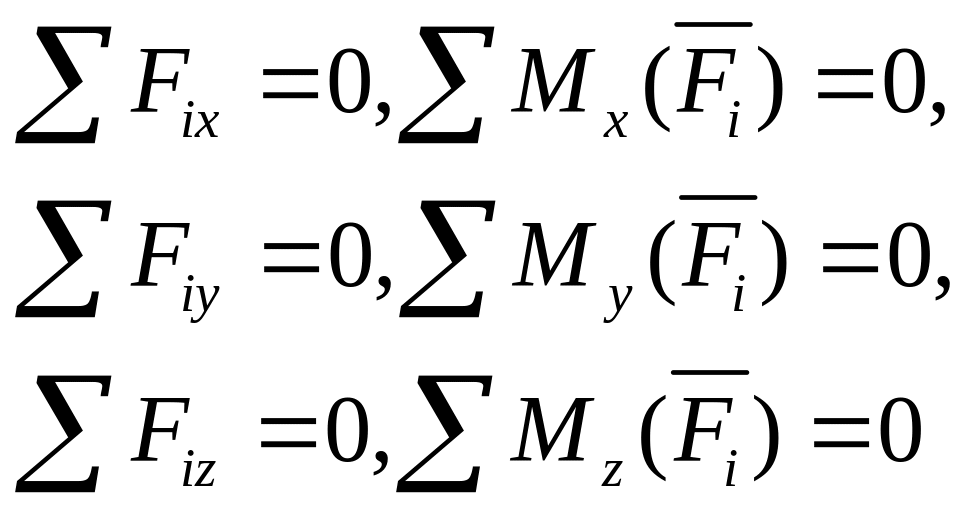
а. Равновесие материальной точки

Материальной точкой называется частица достаточной маленькая, чтобы пренебречь размерами

Чтобы материальная точка находилась в равновесии, необходимо и достаточно, чтобы результирующая всех сил была равна нулю.

а.1 идеальные связи (без трения)

- поверхность идеально гладкая

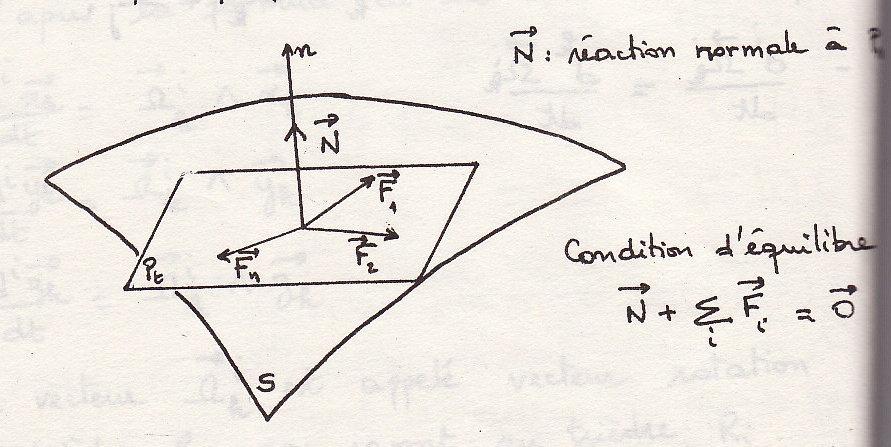
- кривая идеально гладкая

а.2 связи с трением

- сила трения

Рассмотрим тело на горизонтальной поверхности. Тело находится в равновесии, если реакция земли противоположна весу.

Если на тело действует сила F и она мала, тело не движется – силу F уравновешивает сила T.Эта сила статического трения (результирующая всех сил на поверхности контакта).

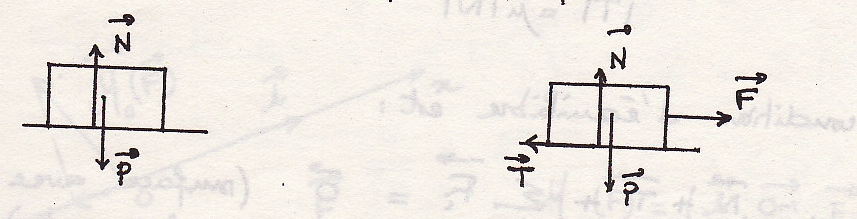
Зависимость Т от силы

Т – максимальная сила трения в статике

Т – сила трения в движении

- коэффициент трения зависит от состояния поверхности

Для равновесия необходимо

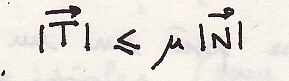
Условие равновесия

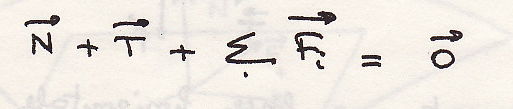
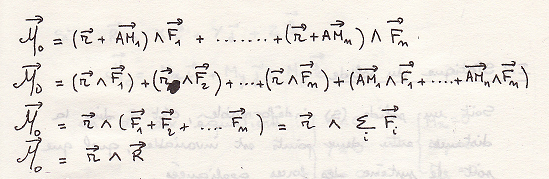
Сложение параллельных сил

Имеем систему параллельных сил в точках

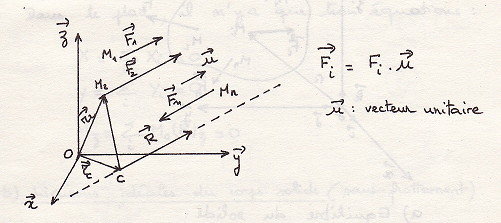
Результирующая сил и результирующий момент параллельных сил

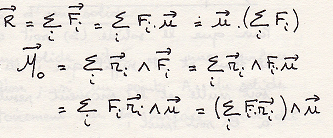
Точка С – центр параллельных сил

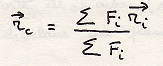
Статика твердого тела

Твердое (недеформируемое) тело – расстояние между двумя точками под действием внешних сил неизменно.

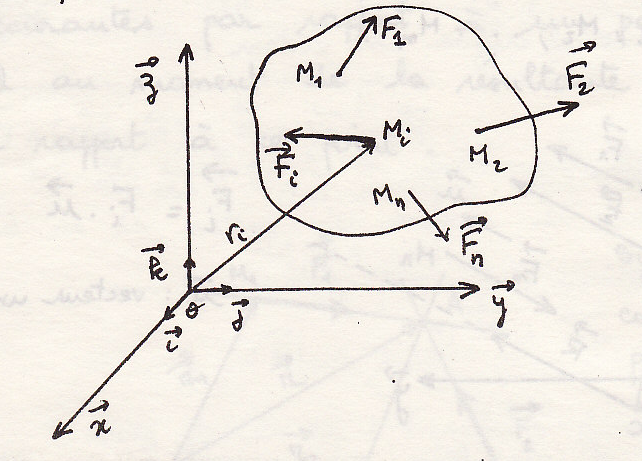
Равновесие тела

Для равновесия твердого тела необходимо и достаточно, чтобы результирующая всех сил и результирующий момент относительно точки равны нули

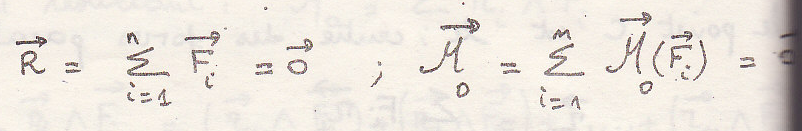
если

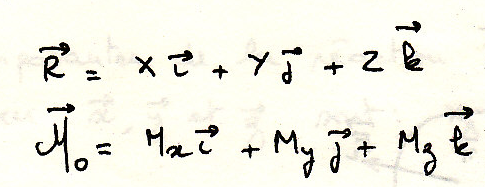
То имеем шесть уравнений

Если число неизвестных не превышает числа уравнений, то система статически определима.

Для плоской системы достаточно трех уравнений

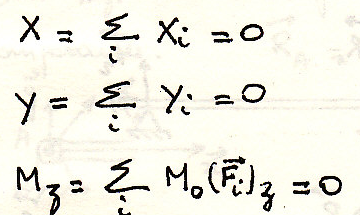
Идеальные связи твердого тела (без трения)

Рассмотрим тело, расположенное на идеально гладкой поверхности

Жесткая опора

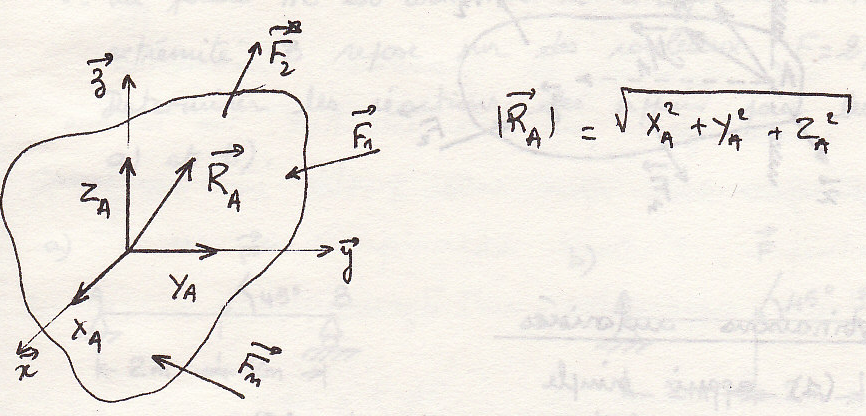
Рассмотрим тело на идеально гладкой поверхности. Если точка А на поверхности \, говорят, что А опора. Реакция перпендикулярна поверхности

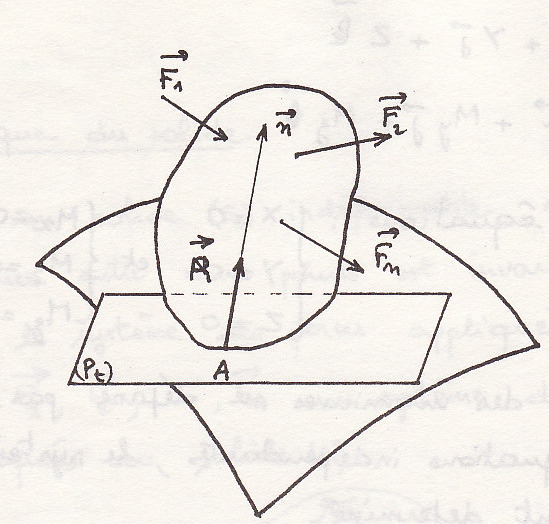
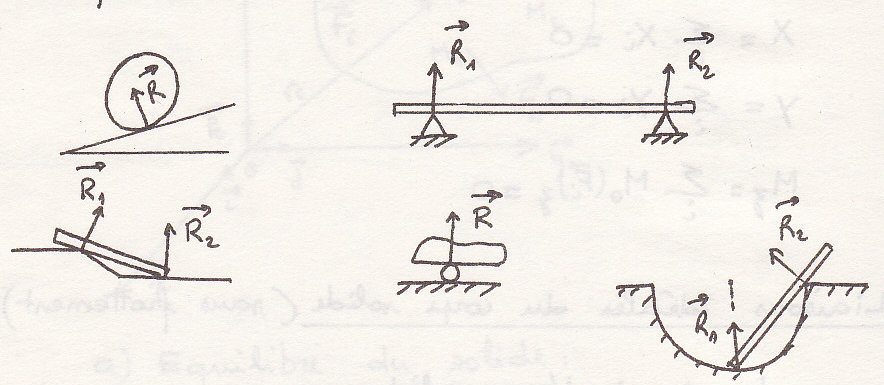
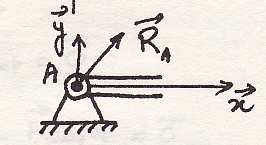
шарнир

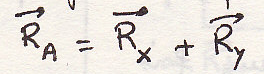
заделка

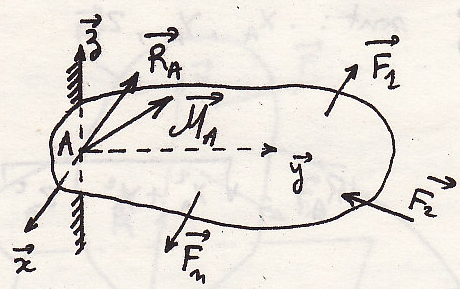
В этом случае имеем реакцию и момент

Разрешенные комбинации

1-простая опора

2- щарнир

3- заделка

Вариации

1 – 2

1 -3

3

Неразрешенные комбинации

2 -2. 2-3. 3-3

Комбинации изостатические

1-1,3,1-2

Комбинации гиперстатические

1-4.1 три и более

Пример

Балка опирается на опоры в точках А и В. Необходимо определить реакции в точках

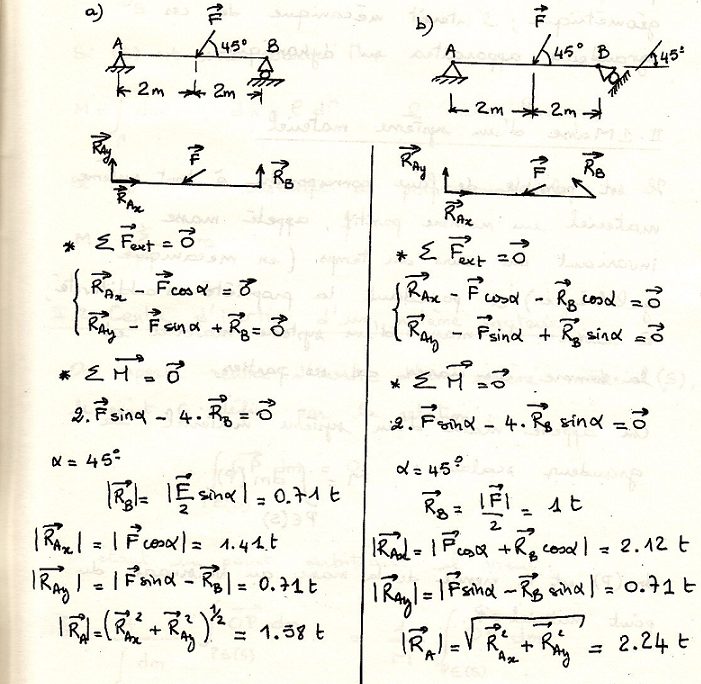
Геометрия масс

Тензорное исчисление, где масса играет основную роль. Понятия этой части нужны в динамике.

Масса материальной системы

Называется массой, неизменной во времени (механика Галилея),обладает свойством аддитив. Масса – сумма масс частей

Масса скалярная величина

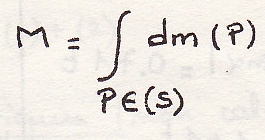
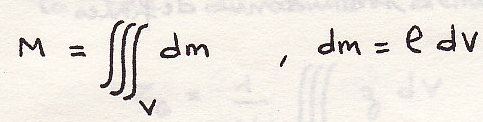объем поверхность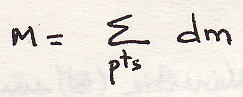

Центр инерции тела

Центром масс называется

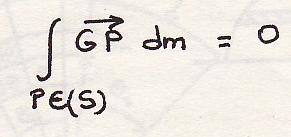
О – любая точка

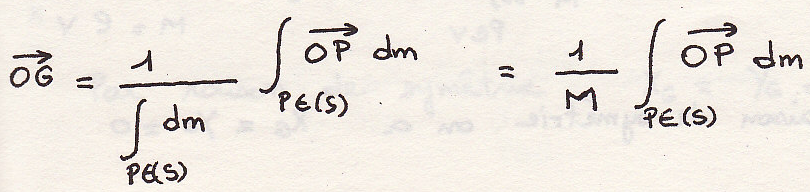
Координаты точки

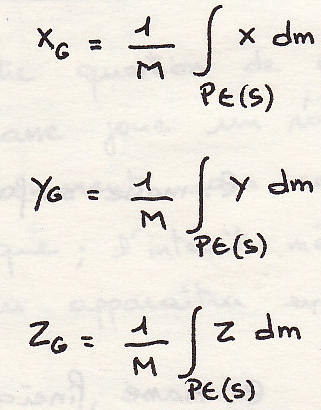
Пример

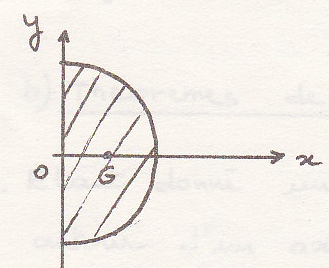
Определим центр инерции тела

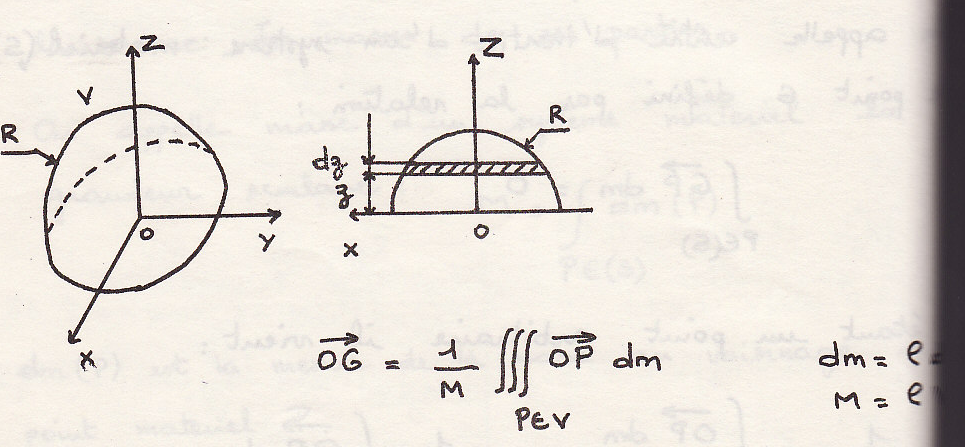
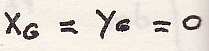
Центр инерции

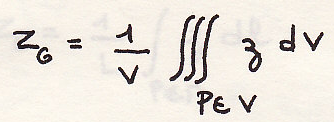
элементарный объем

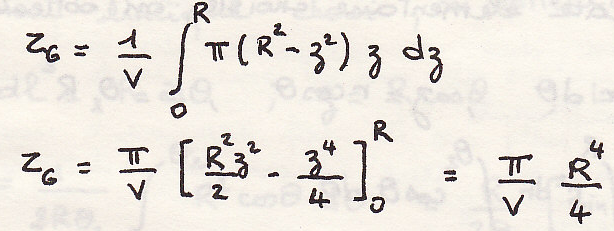
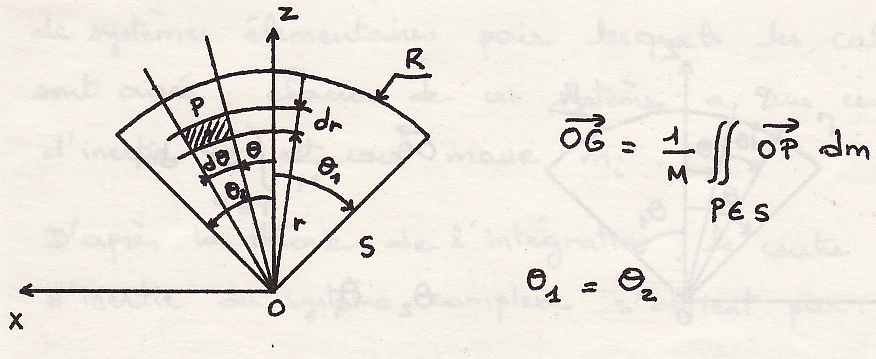
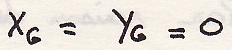
Центр инерции

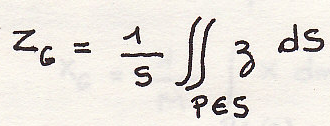
Воспользуемся полярной системой координат

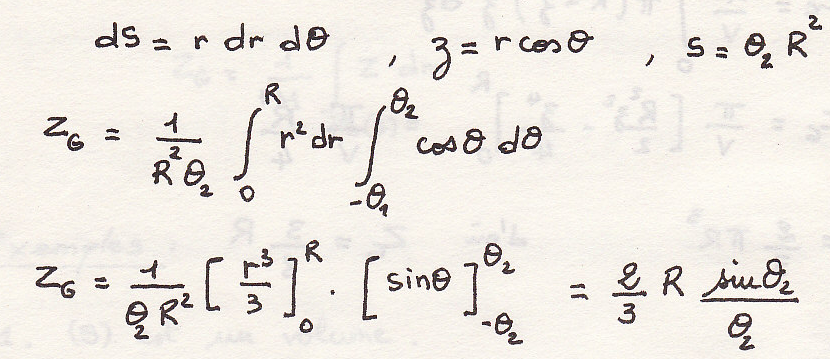
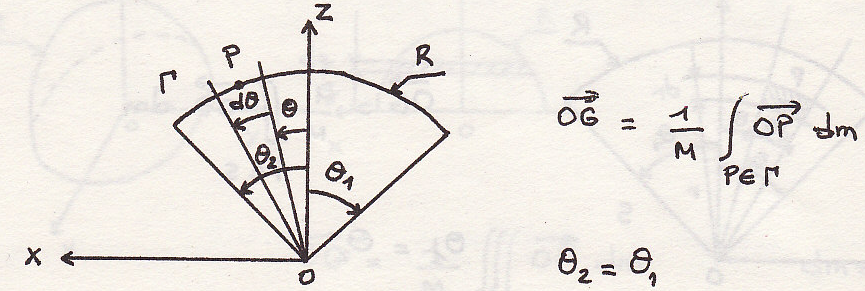
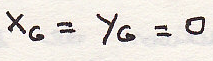
Центр инерции

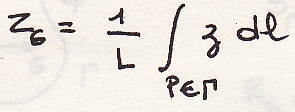
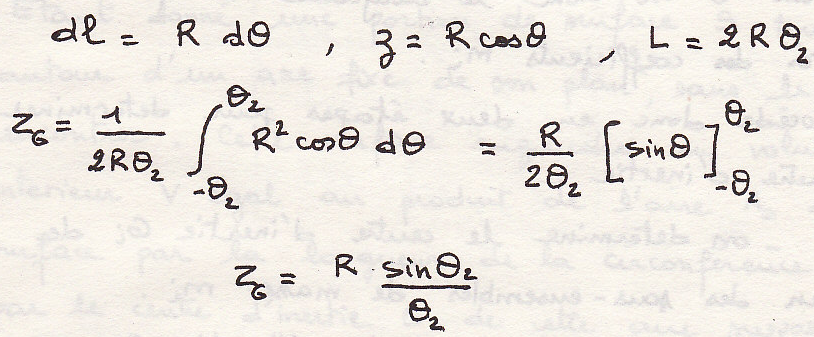
Общий случай

Зная центр составляющих систему интегрируя получим

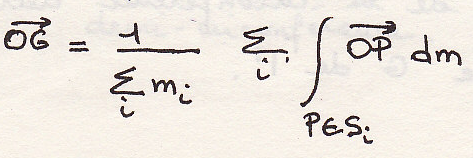
где

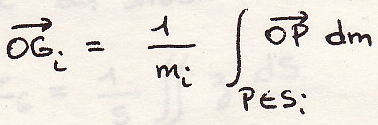
окончательно

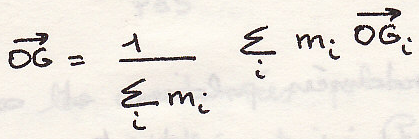
И так два этапа нахождения центра инерции

- определяем ЦИ элементов системы

- определяем ЦИ системы

Теорема Гульдена

Гульден дал доказательство двух теорем, позволяющих легко определить поверхность и объем тела, полученного от вращения плоской фигуры около оси, лежащей в ее плоскости и ее не пересекающей.

Теорема 1 –поверхность, полученная от вращения плоской линии около оси, лежащей в плоскости линии и не пересекающей ее, равна длине линии, помноженной на длину окружности, которую описывает центр тяжести этой линии.

Теорема 2 – объем, полученный от вращения плоской фигуры около оси, лежащей в ее плоскости и не пересекающей ее, равен окружности, описанной центром тяжести площади фигуры, помноженной на площадь фигуры

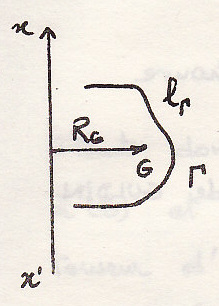
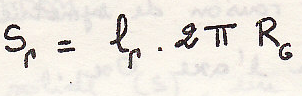
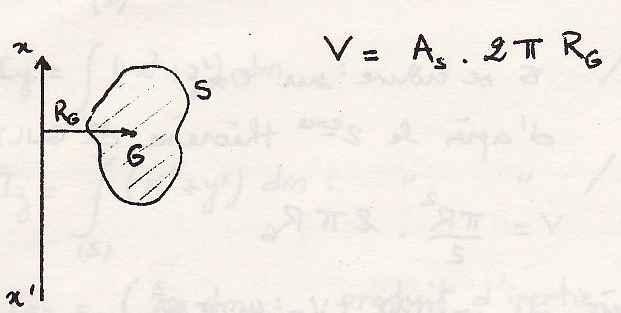
пример

1. Определить ЦИ

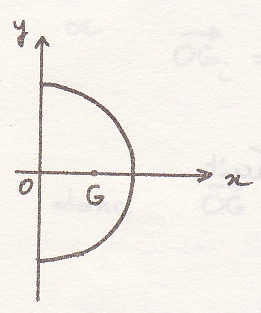
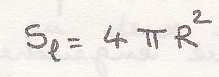
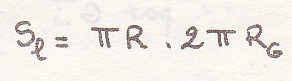
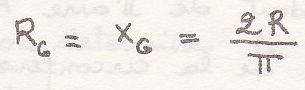
2. Определить ЦИ

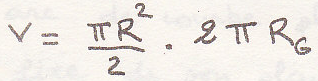
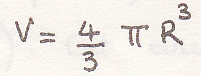
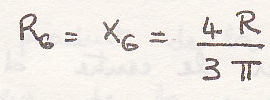
Тензор инерции

Определение

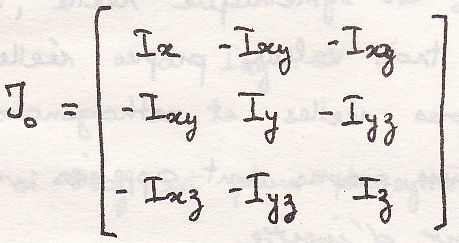
где

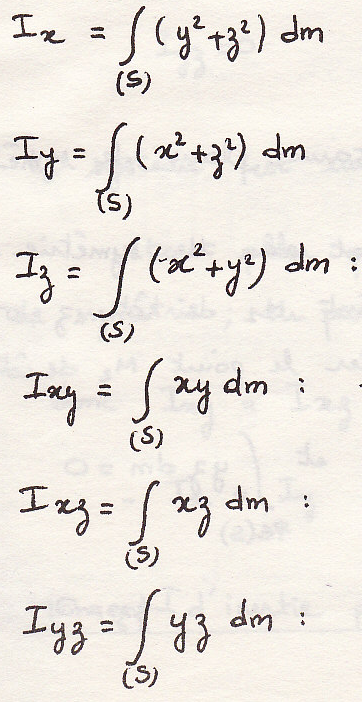
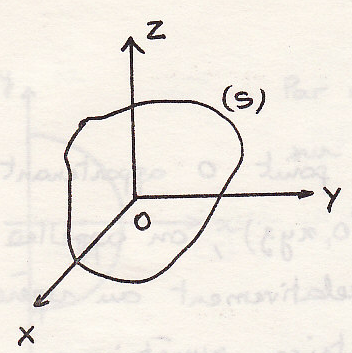
Особый случай

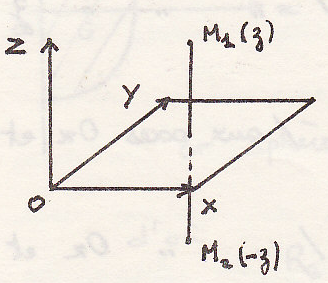
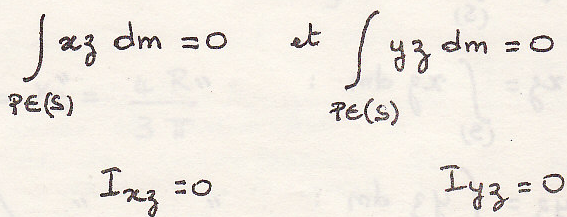
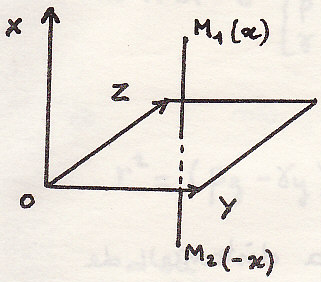
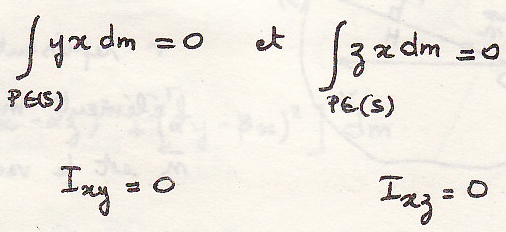
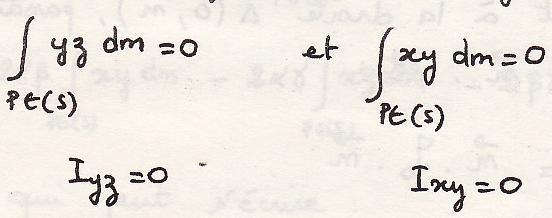
2.

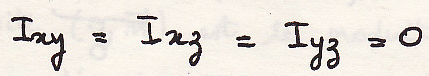
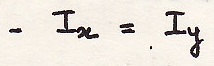
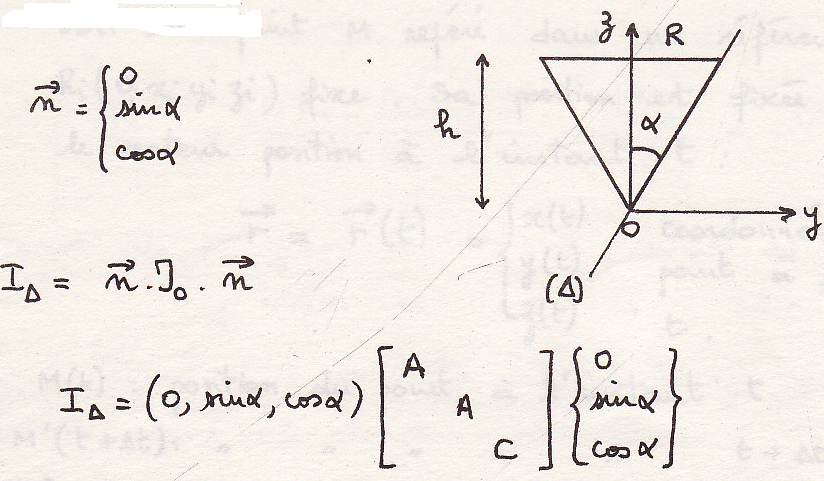
Момент инерции относительно прямой

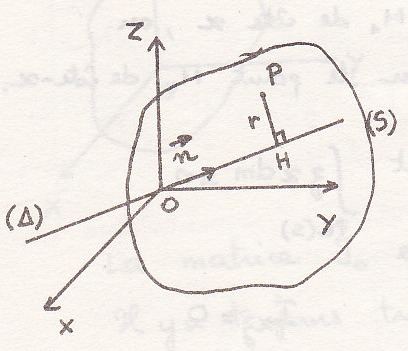
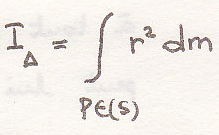
пример

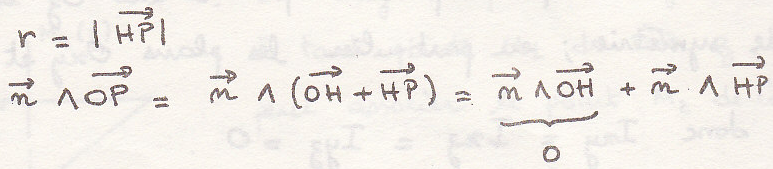
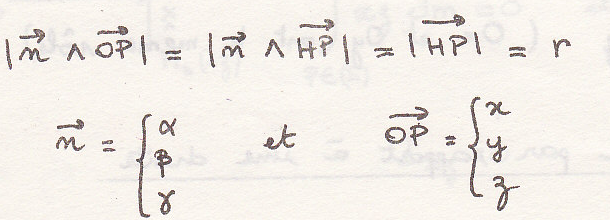
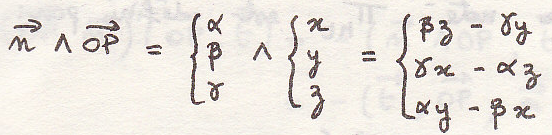
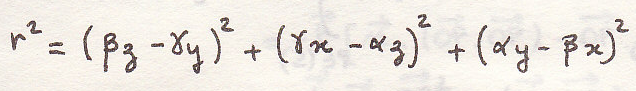
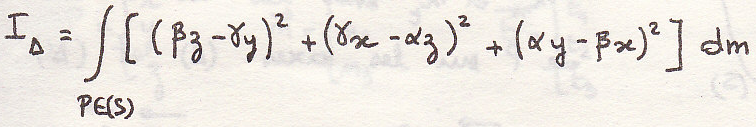
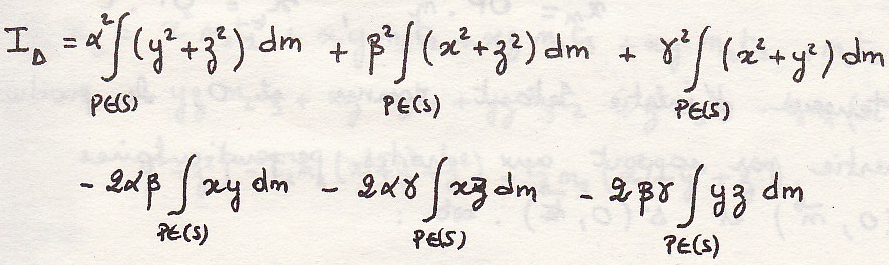
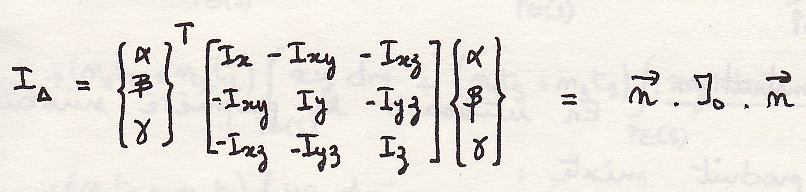
Произведение ЦИ относительно двух перпендикулярных прямых

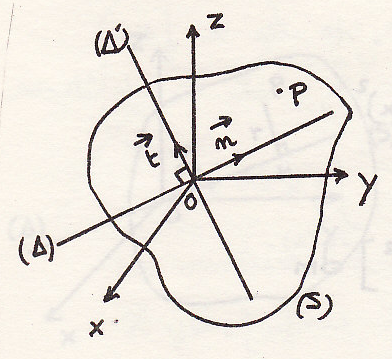
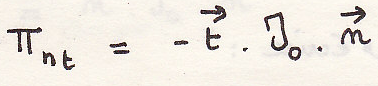
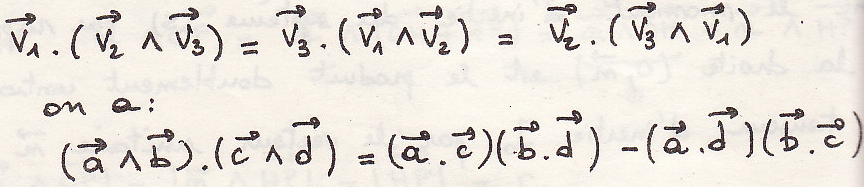
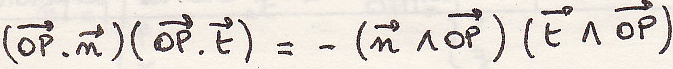
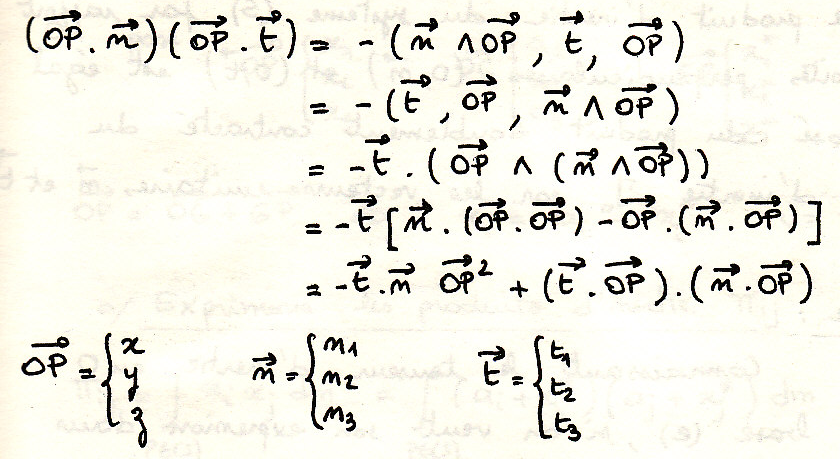
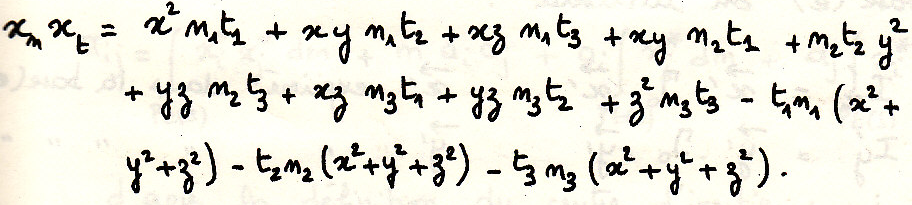
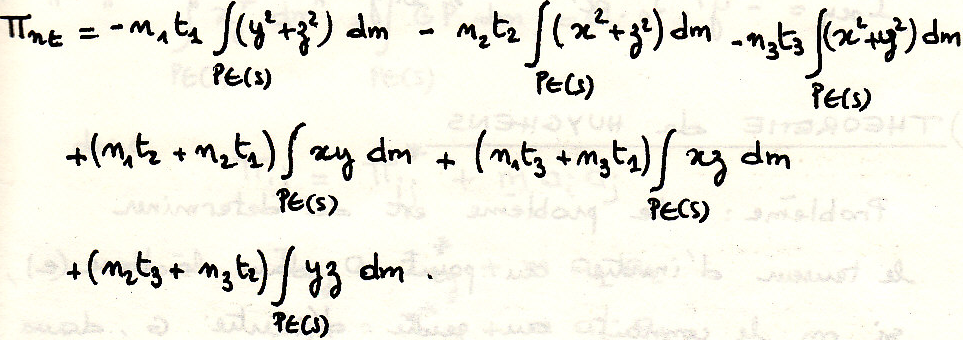
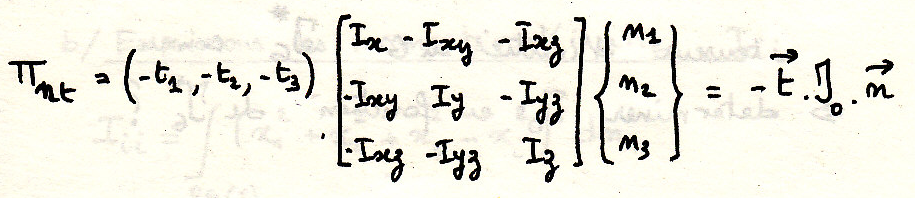
примечание

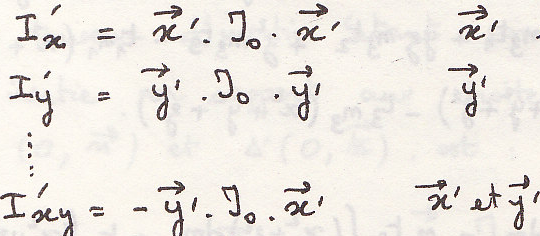
Теорема Гульдена

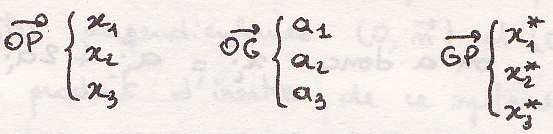
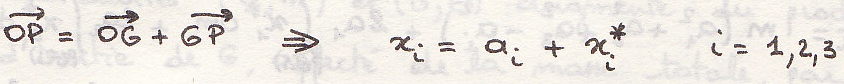
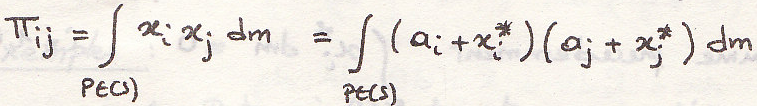
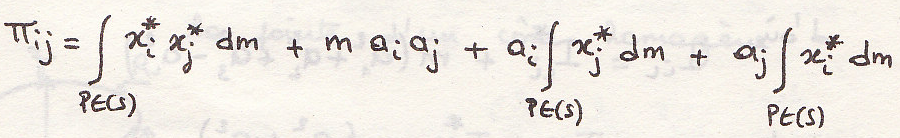
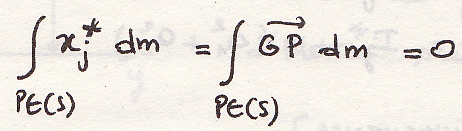
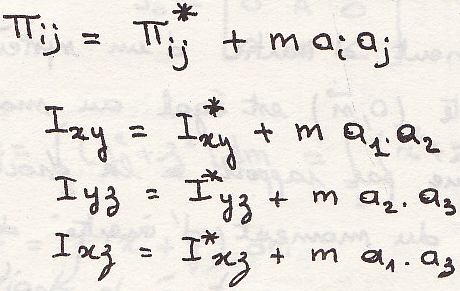
Момент инерции

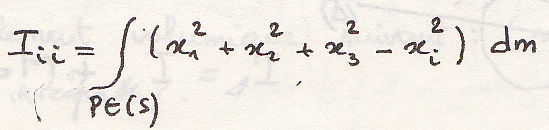
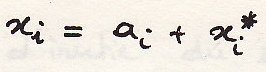
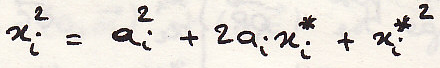
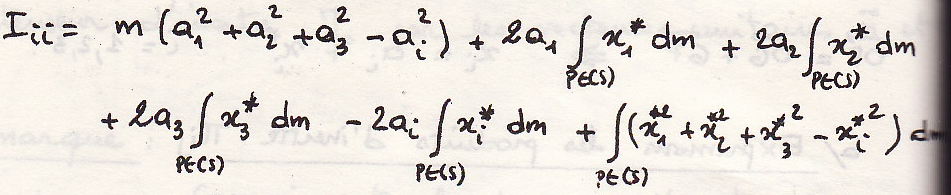
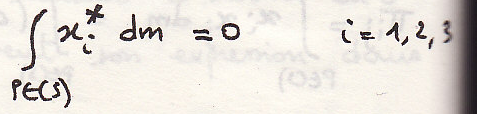
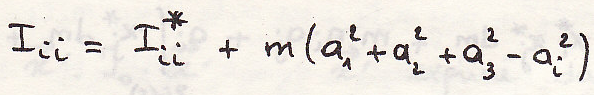
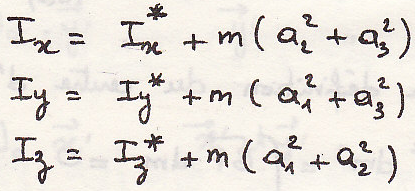
Теорема Гульдена

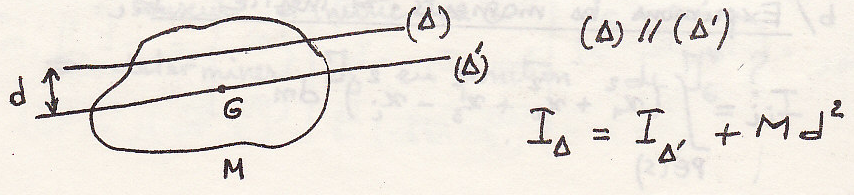
пример

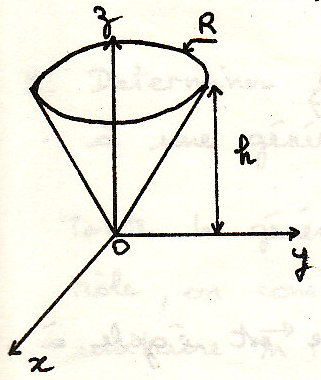
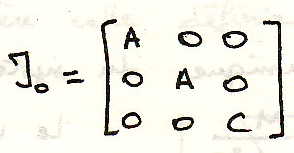
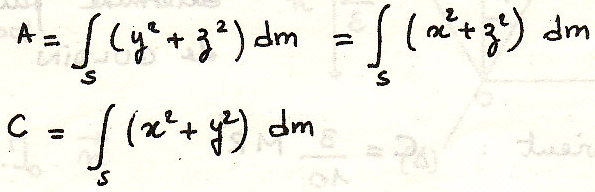
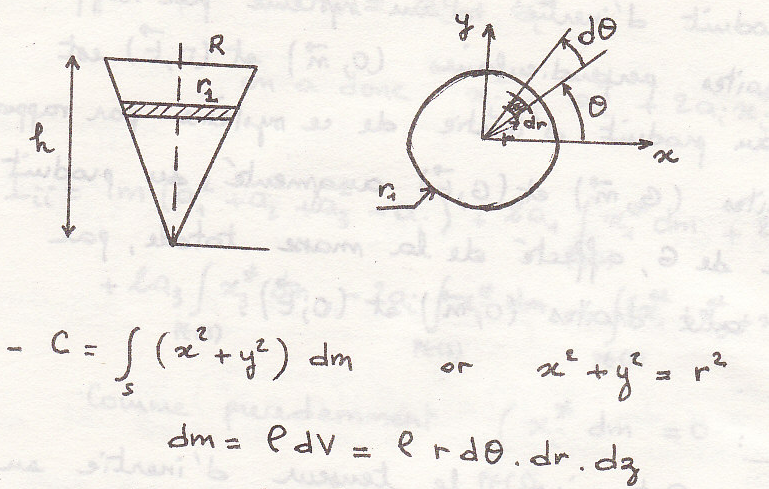
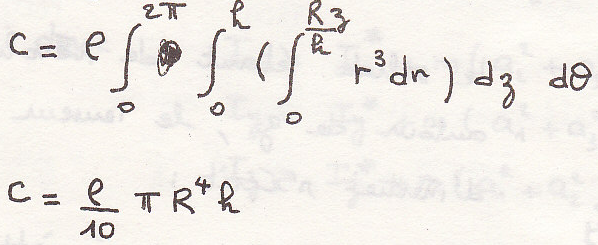
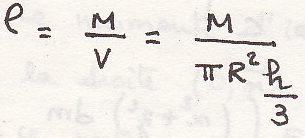
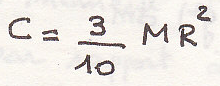
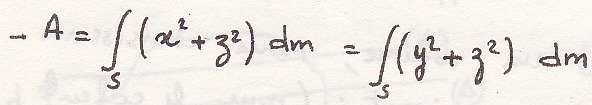
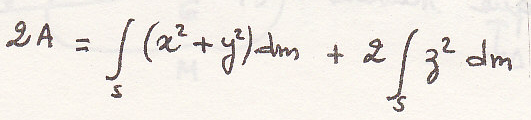
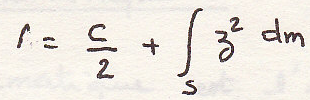
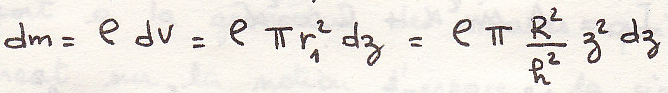
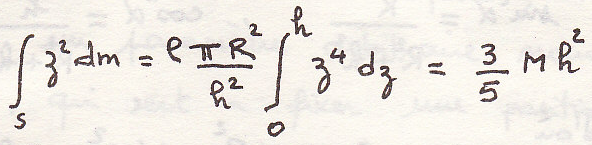
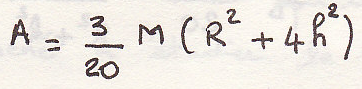
Определим момент инерции относительно

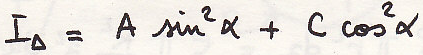
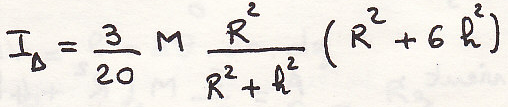
Кинематика

кинематика изучает движение тел без учета причин его вызывающих

Траектория, скорость и ускорение точки

- траектория

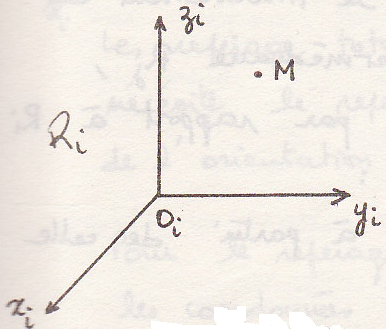
Пусть точка М в системе координат. Ее положение в данный момент времени определяется вектором.

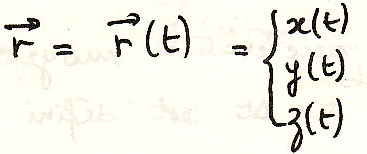
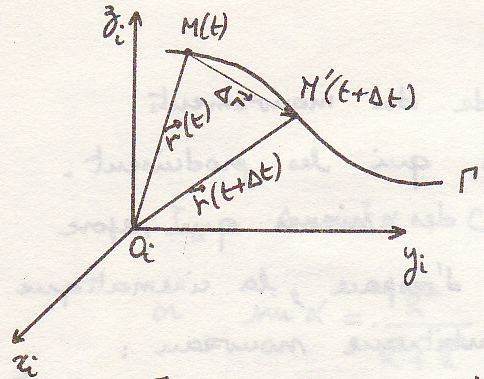
Г – траектория движения

- если Г прямая – движение прямолинейно

- если Г кривая – движение криволинейно

Вектор скорости и ускорения

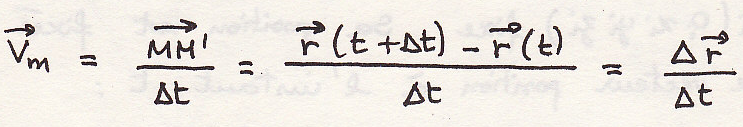
Вектор ускорения

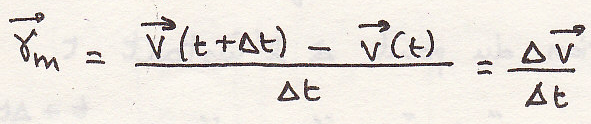
определения

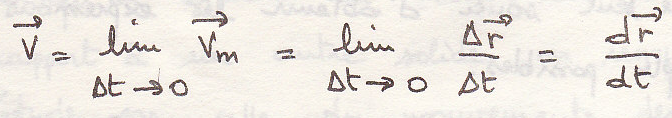
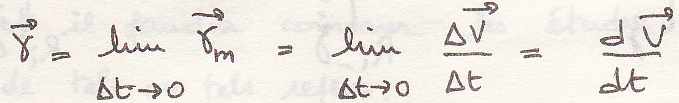
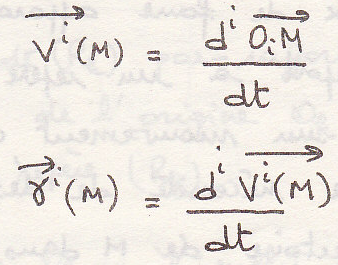
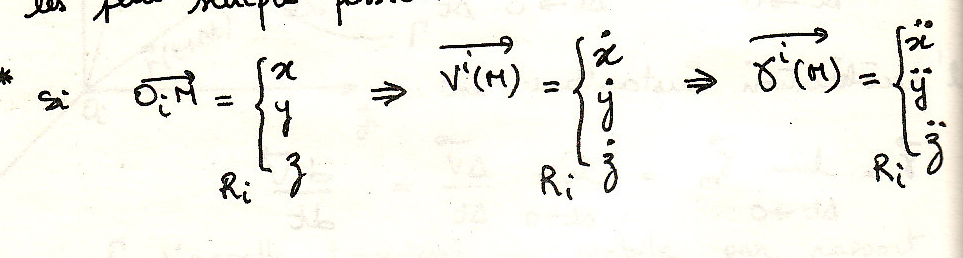
Кинематика тела

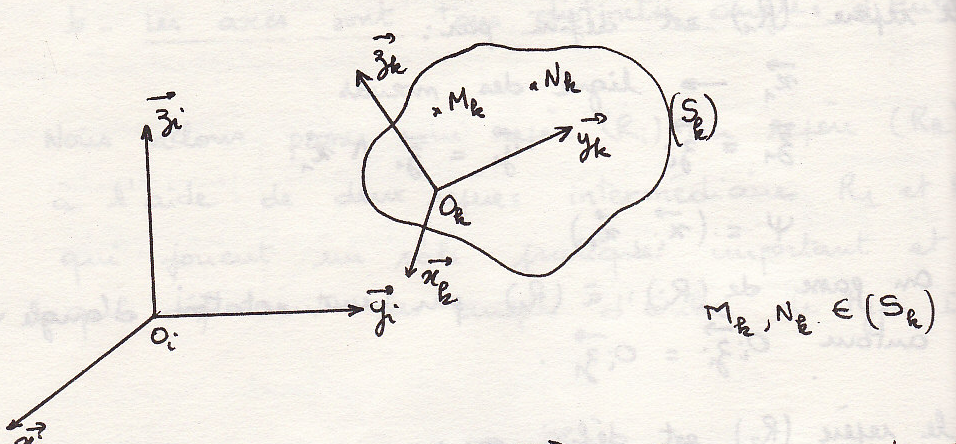
Напомним, что твердое тело это ансамбль элементов, расстояние между которыми неизменно во времени

Подвижная система координат относительно неподвижной

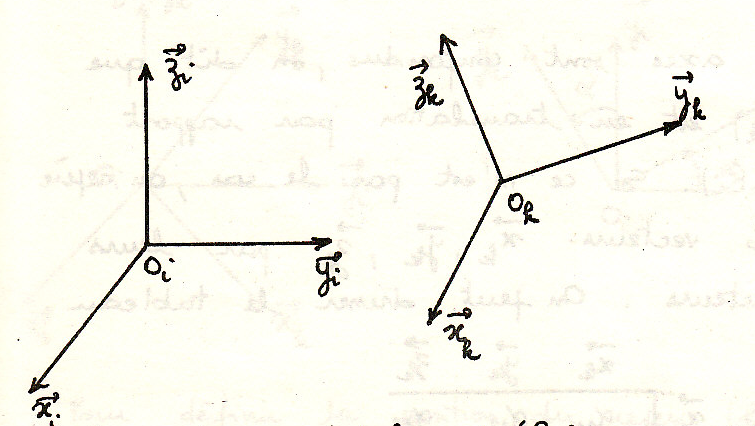
Необходимо знать

Для случая

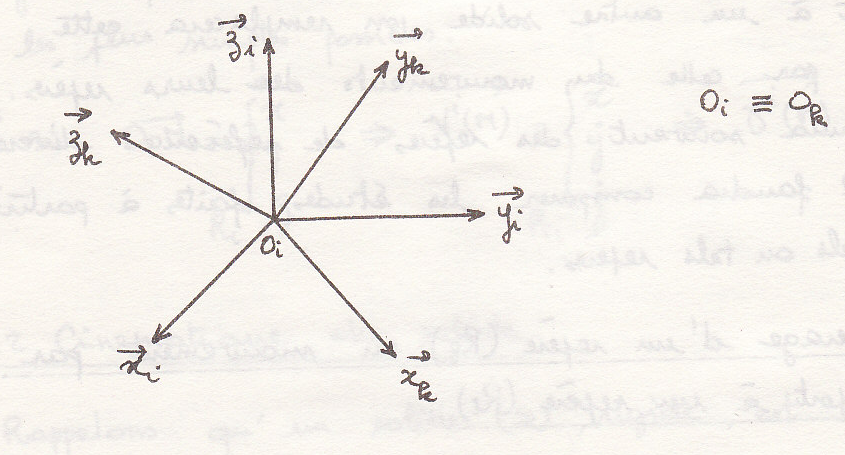
Можно записать

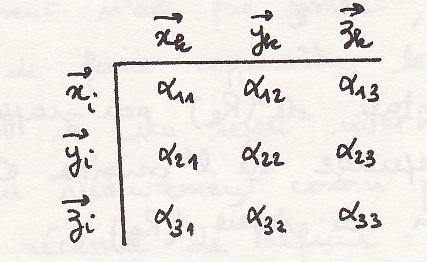
Матрица

Матрицей называется

Проще определить положение углами Эйлера

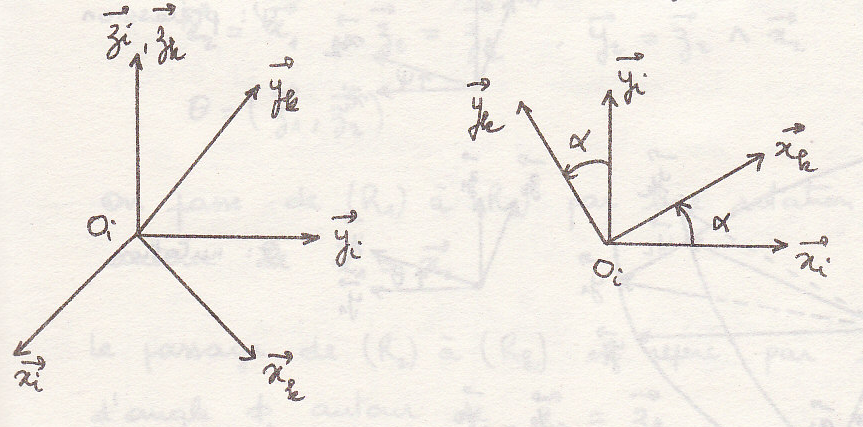
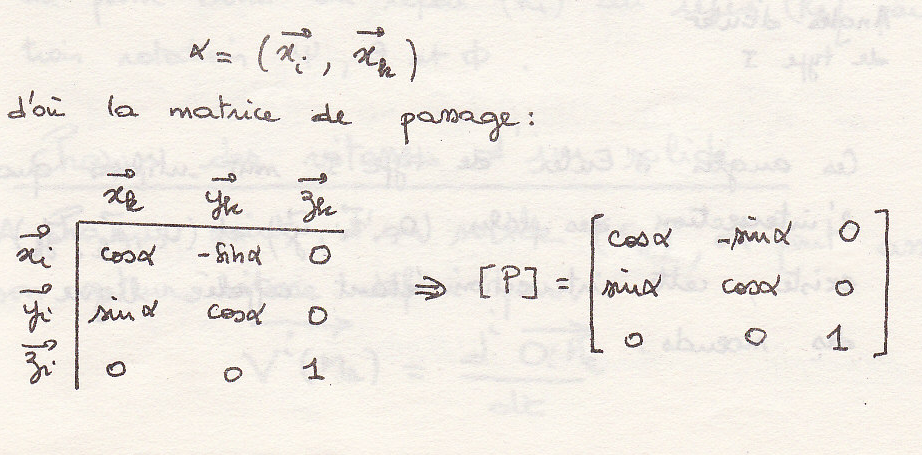
Углы Эйлера

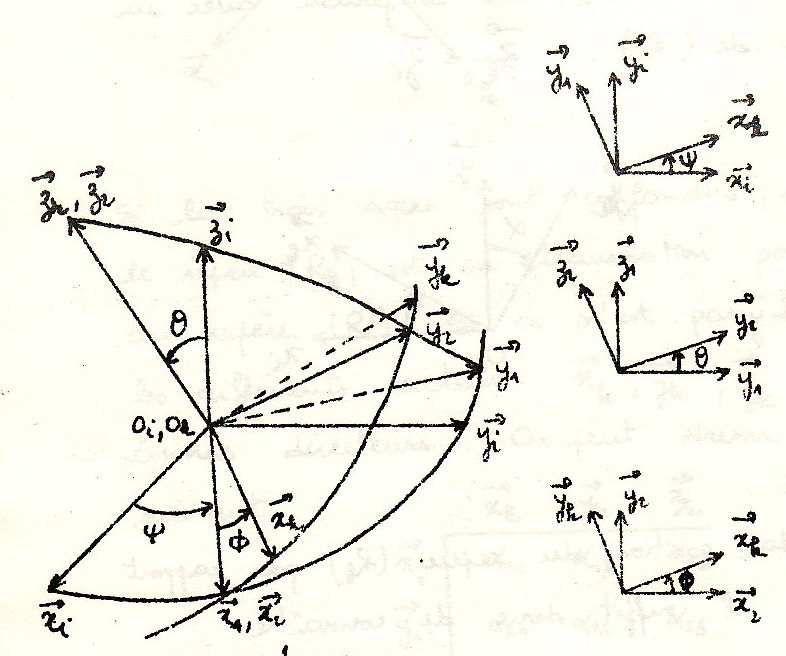
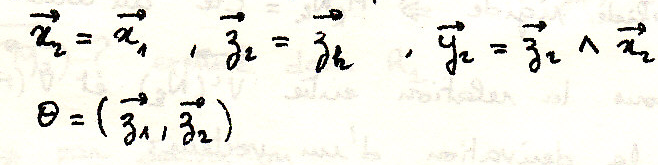
Поле скоростей тела

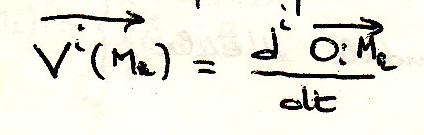
Твердое тело движется

Найдем отношение между скоростями точек

Дифференцируя вектора

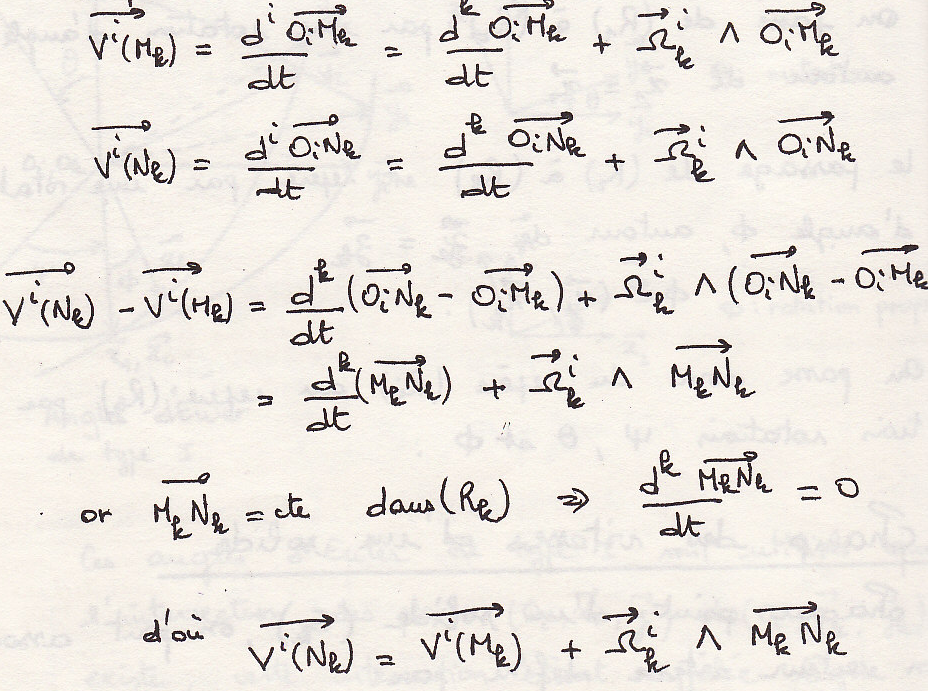
пример

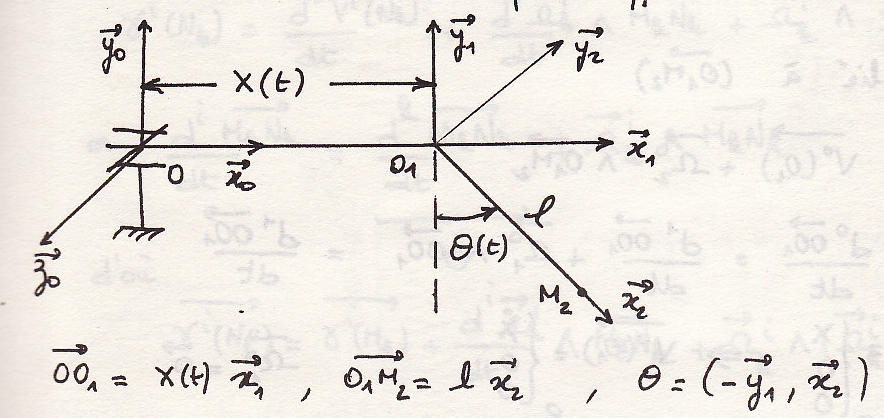
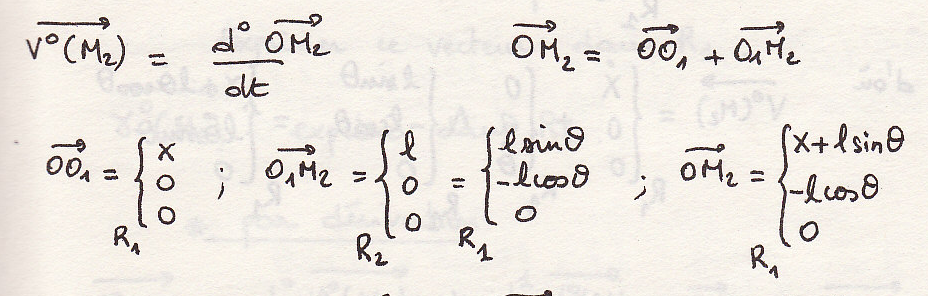
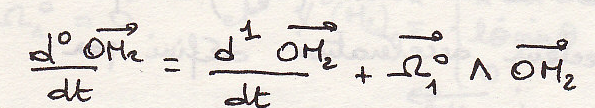
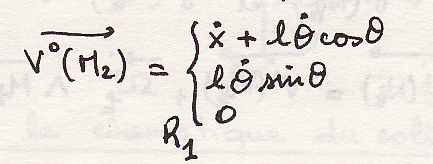
Кинематика тела

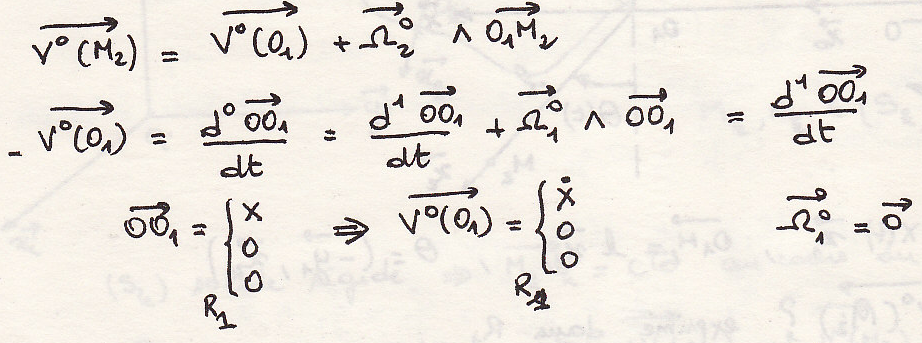
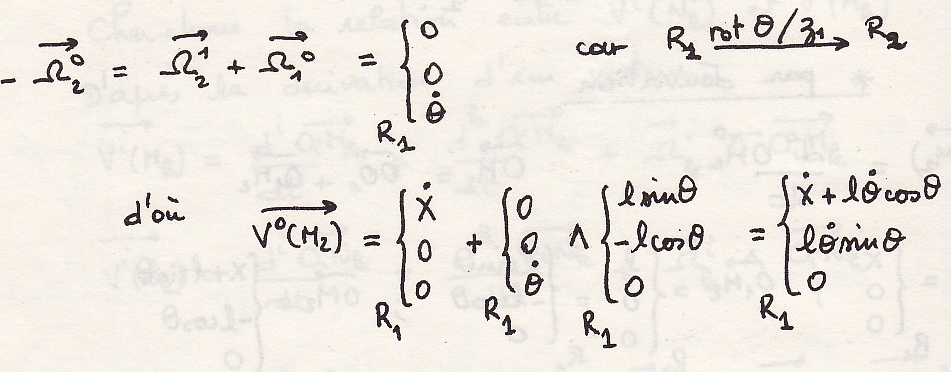
Поле ускорений тела

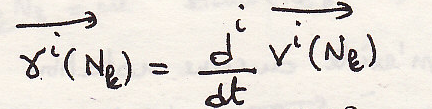
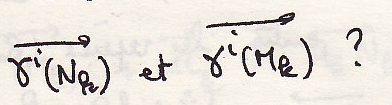
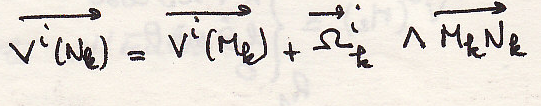
Пример

Определите вектор ускорения точки с помощью углов Эйлера

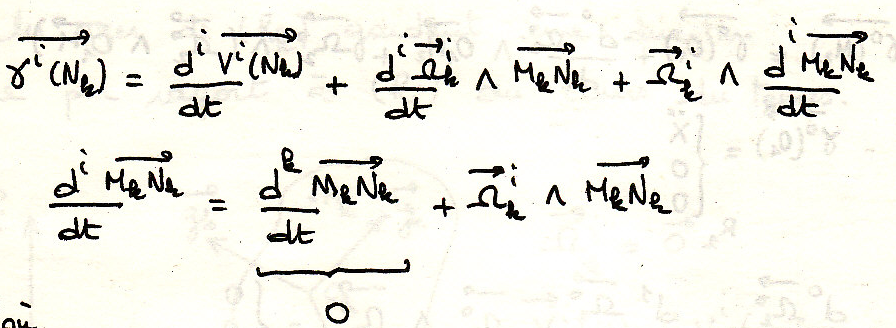
пример

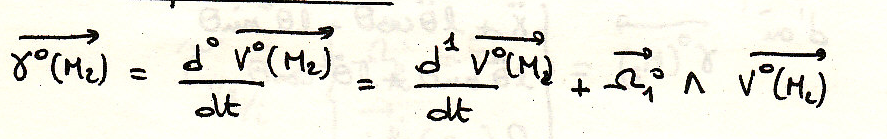
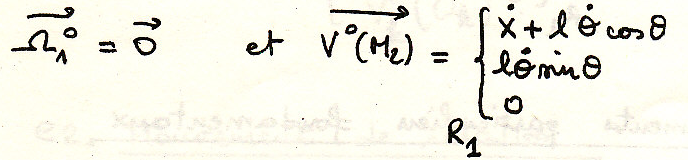
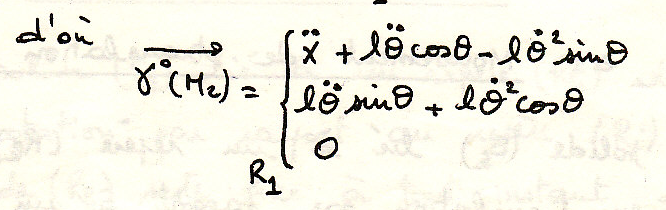
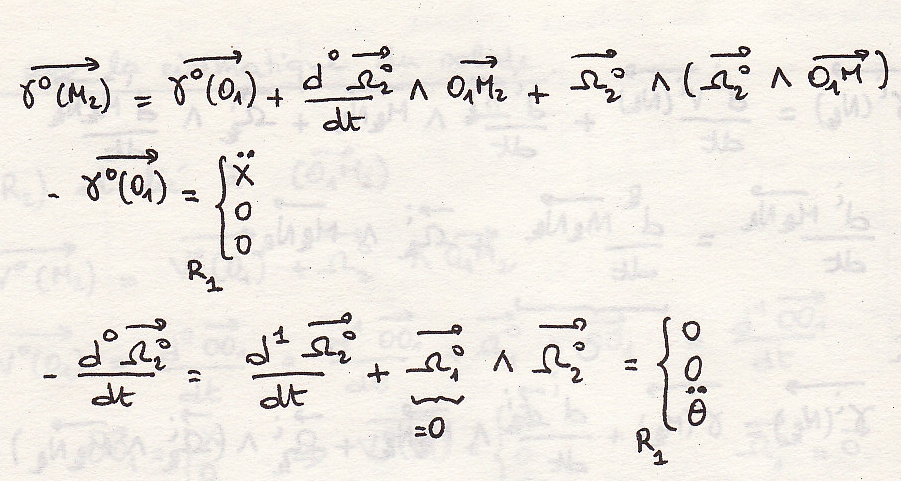
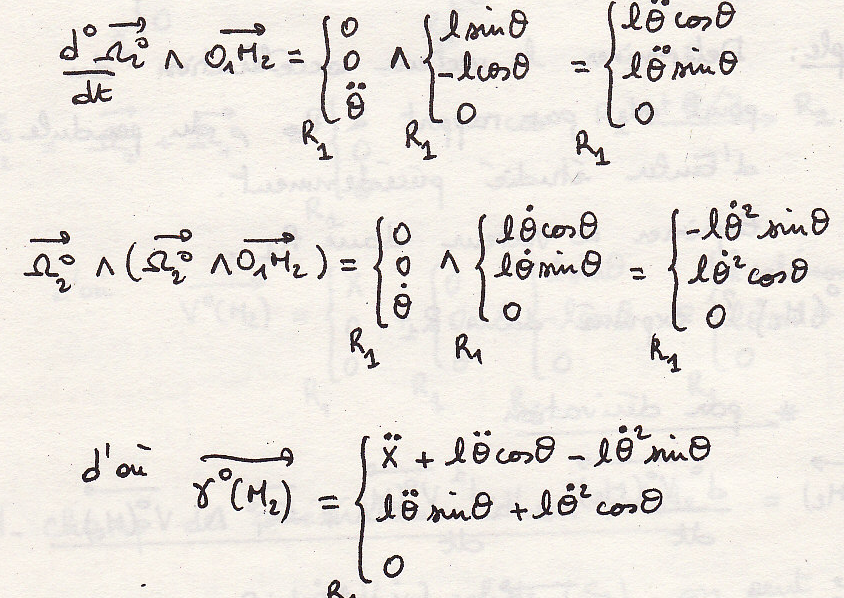
Особые случаи движения

Прямолинейное движение

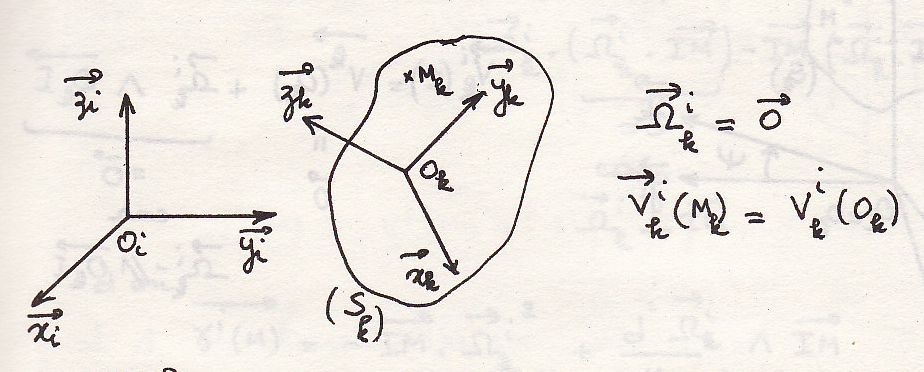
В случае все точки движутся с одной и тоже скоростью и ускорением. Вектор вращения равен нулю.

Торсор скорости

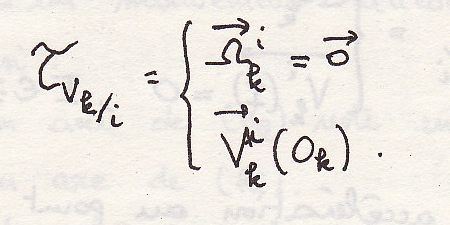
Вращательное движение

В случаи вращения торсор скорости

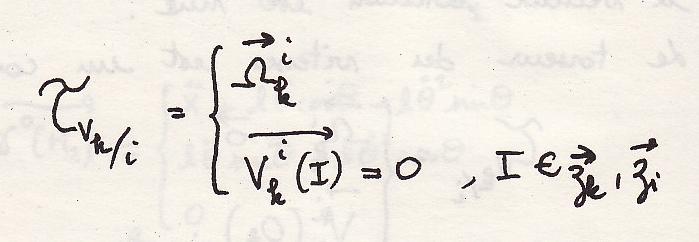
Определим ускорение точки

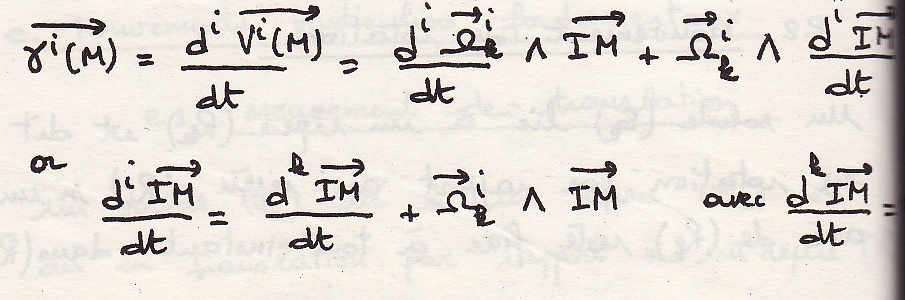
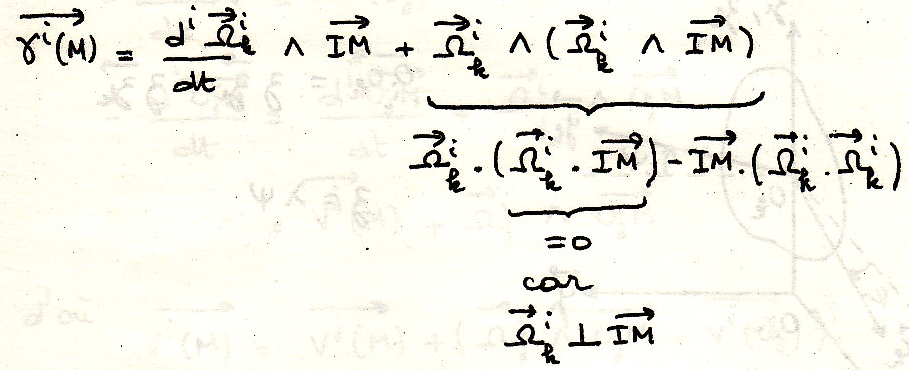
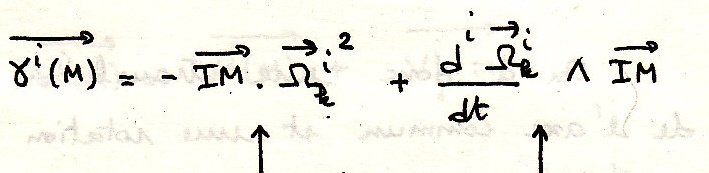
Нормальное ускорение касательное ускорение

Винтовое движение

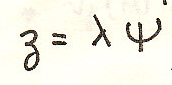
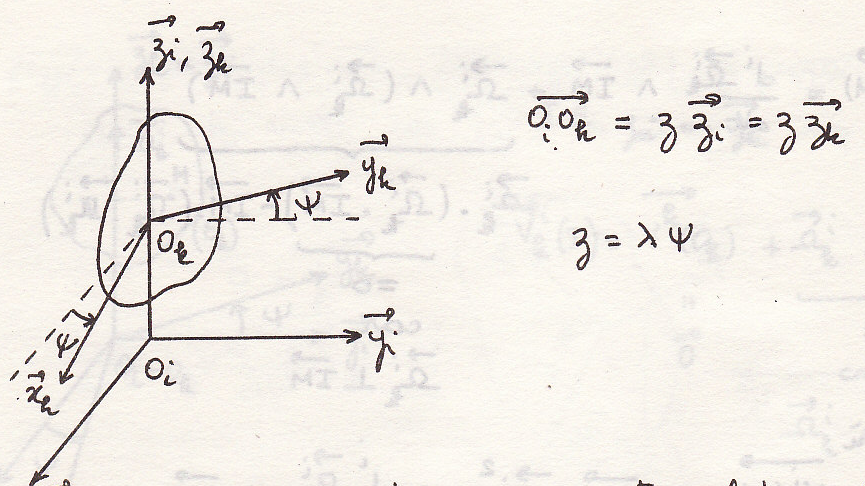
Сложение движений

Сложение скоростей

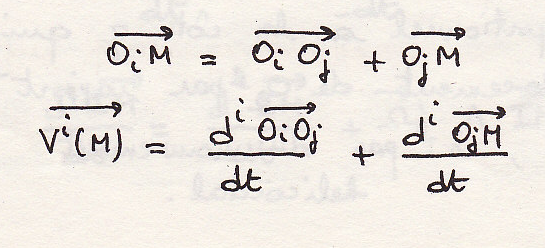
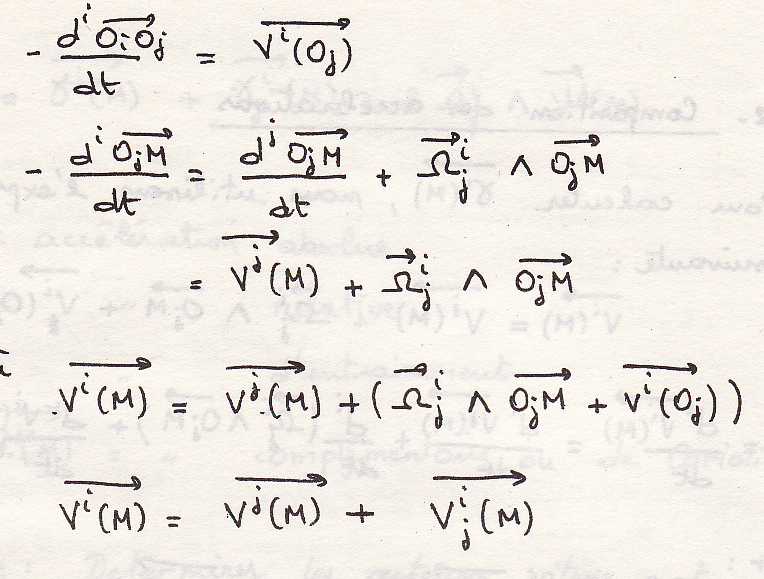
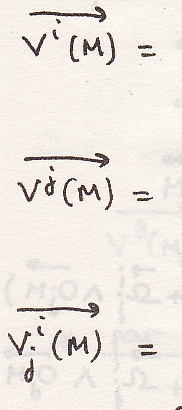
Свойства векторов

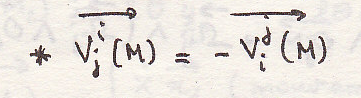
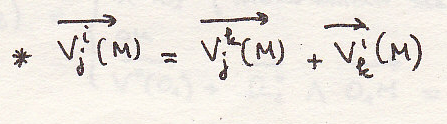
Сложение ускорений

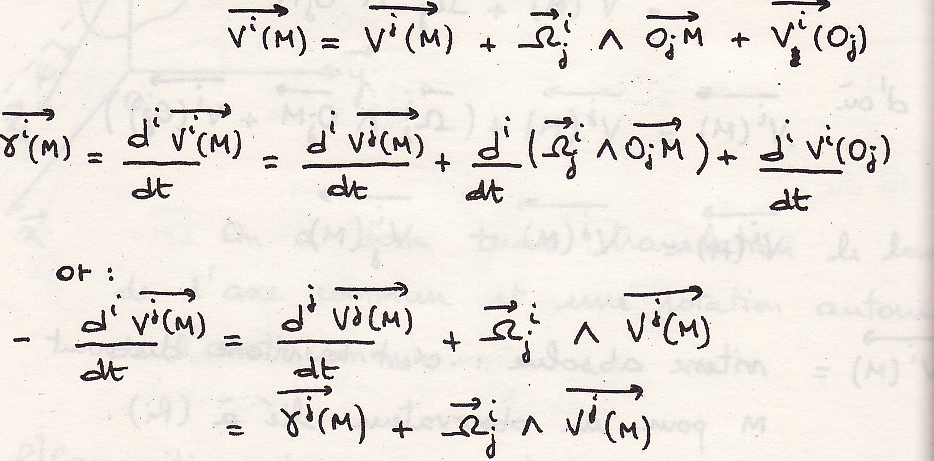
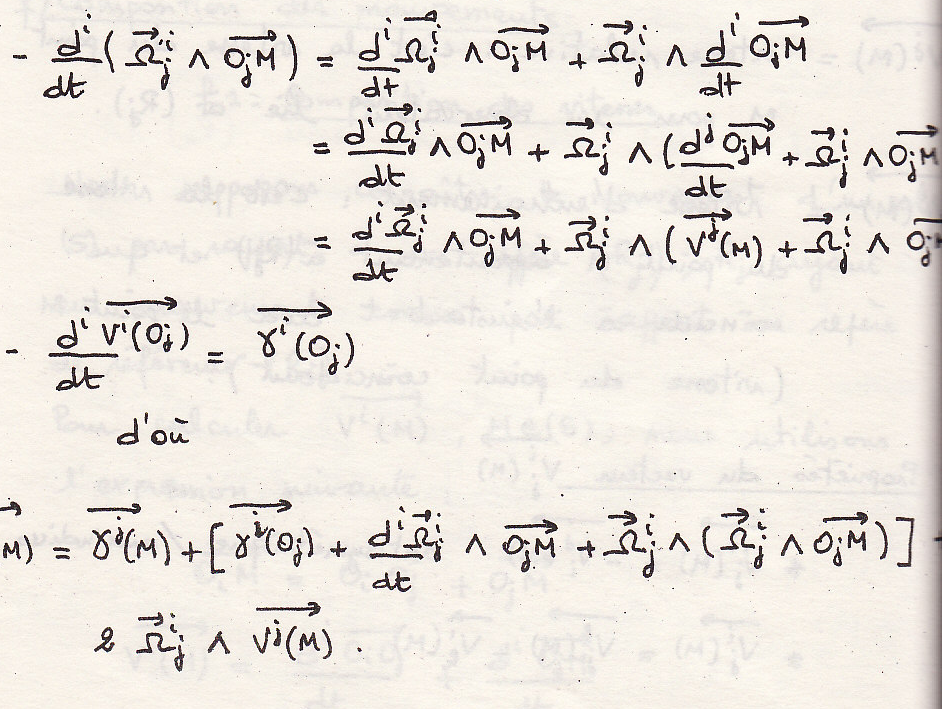
Окончательно:

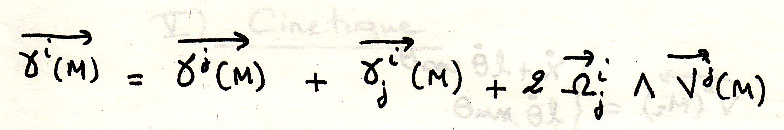
где

абсолютное ускорение

- относительное ускорение

- переменное ускорение

дополнительное ускорение или ускорение Кориолиса

Пример . Определитель абсолютные скорости и ускорения точки маятника Эйлера и представить их вектора в системе координат , используя сложение движений.

1. Определение скоростей .

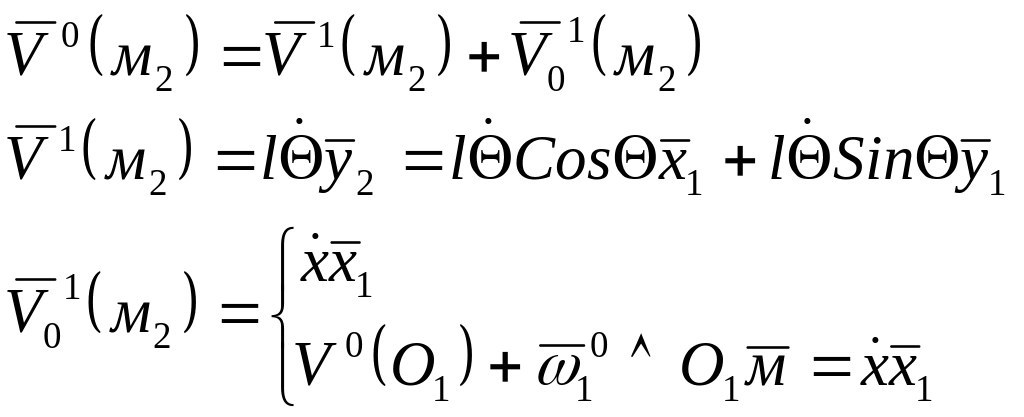
поступательное движение R1 относительно R0

Итак.

2. Определение ускорения.

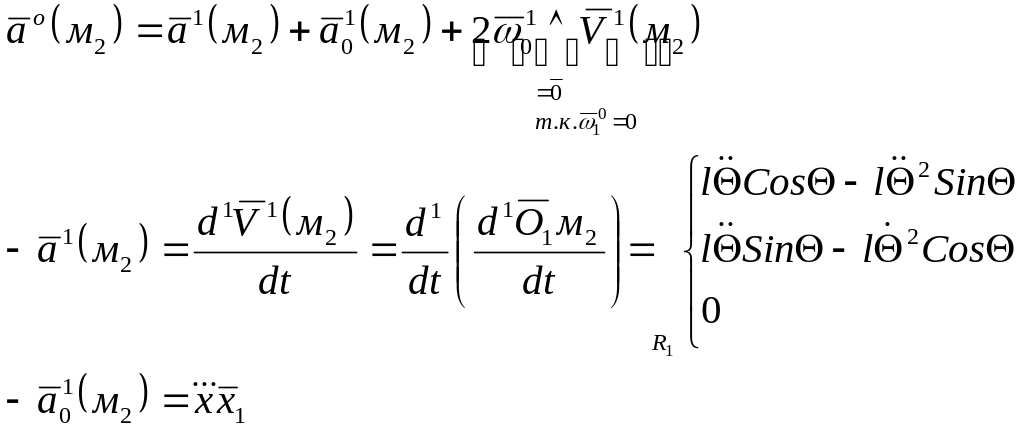
Окончательно.