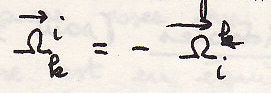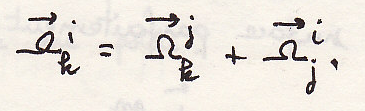Бадалов В.В.

просто

теормех

Санкт-Петербург

2013

Мы давно и много говорим о вхождении России в международное образовательное пространство. Однако содержание и методика преподавания основных технических дисциплин в стране не соответствуют этому пространству.

Автор на опыте преподавания за рубежом предлагает курс «Теоретическая механика».

Книга будет полезна тем, кто преподает и изучает Теоретическую механику или предполагает работать за рубежом.

Содержание

1. элементы векторной алгебры

- определение вектора

- аналитическое представление вектора

- сложение векторов

- скалярное произведение двух векторов

- векторное умножение двух векторов

- смешенное произведение трех векторов

- двойное произведение трех векторов

- производная вектора в неподвижной системе координат

- производная вектора в подвижной системе координат

2. статика

2.1 основные положения статики

- равновесие материальной точки

идеальные связи

связи с трением

- система сил

момент силы относительно точки

момент силы относительно оси

теорема Вариньона

сложение параллельных сил

2.2. статика тела

равновесие тела

идеальные связи твердого тела

опора

шарнир

заделка

2. геометрия масс

масса материальной точки

центр инерции материальной системы

случай сложной системы

теорема Гульдена

тензор инерции

определение

особый случай

момент инерции относительно прямой

произведение инерции относительно двух перпендикулярных прямых

теорема Гуйгенса

пример

2. Кинематика

кинематика точки

траектория

вектор скорости и вектор ускорения

кинематика тела

движение относительно системы координат

углы Эйлера

поле скоростей тела

поле ускорений тела

особые случаи движения

перемещение

вращение

винтовое движение

сложение движений

сложение скоростей

сложение ускорений

5. Кинетика

торсор кинетический

торсор динамический

энергия кинетическая

6. Основные теоремы динамики

основной закон для системы

теорема результирующей кинетической энергии

теорема динамического момента

теорема кинетической энергии

Страницы истории

- 384-322 г. до н.э. философ Аристотель ввел понятие «механика»

-287-212 г. до н.э. Архимед заложил основы механики

- 1355г. в Париже по праздникам разрешено преподавать геометрию

- Николай Коперник(1473-1543) сформулировал гелиоцентрическую систему мира

- Кеплер (1571-1630)открыл законы для времени обращения и скорости планет

-Галилей (1564-1642) основатель научных методов исследований вместо схоластических рассуждений

-Христиан Гюйгенс (1629-1695) дал ряд теорем о центробежной силе, теории удара, физического маятника

-Исаак Ньютон (1642-1727) –основатель классической механики. Сформулировал аксиомы механики, вел понятие массы, открыл закон всемирного тяготения

1637г. – Рене Декарт предложил плоскую систему координат

1690г. – Лейбницем введено название «динамика»

1743г. – Д`Аламбер предложил термин «инерция»

1804г. – Луи Пуансо создал теорию пар и ввел термины: пара, плечо, момент

1829г. – термин работа введен Кариолисом

1834г. – кинематика, предложено Ампером

1846г. – термин вектор в математическом понятии появился в «Символической геометрии» Гамильтона

1862г.- термины «тангенциальное» и «нормальное» ускорения появились в печати у Резаля

Механика – (гр. mechanike – орудие, машина) наука о перемещении и равновесии материальных тел.

1. Элементы векторной алгебры.

В физике, математике, технике много величин носят векторный характер. Векторное исчисление создано в Х1Х веке трудами ученых разных стран (Гамильтон, Мёбиус, Грассман, Максвелл, Гиббсон и др.). Оно позволяет часто значительно сократить вычисления, проще выразить связь между различными физическими величинами.

1. Определение вектора

В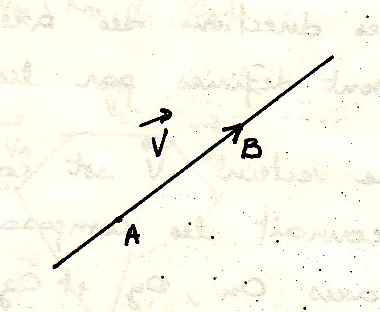 ектор (лат.vector – везущий, несущий) – направленный отрезок прямой, имеющий начало и конец.

Вектор определяют:

- линия действия

- начало и конец (точки А и В)

- направление

- модуль

Модуль – численное значение вектора.

Обозначение: .

Классификация:

Свободный вектор – не имеет точки крепления и линии действия. Определены только направление и модуль. Можно переносить в пространстве параллельно своему начальному положению.

Скользящий вектор – началом вектора может быть любая точка на линии действия

Связанный вектор – определены все параметры вектора

Единичный вектор – модуль равен единице.

Нулевой вектор – модуль равен нулю.

Два вектора равны, если модули одинаковы и направления совпадают.

Коллинеарные вектора – лежат на одной прямой либо на параллельных прямых.

Компланарные вектора – расположены на прямых, параллельных одной и той же плоскости.

Сравнивать можно только вектора одинаковой размерности.

Аналитическое представление вектора.

Имеем прямоугольную систему координат и единичные вектора: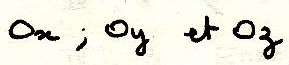

Вектор полностью определен:

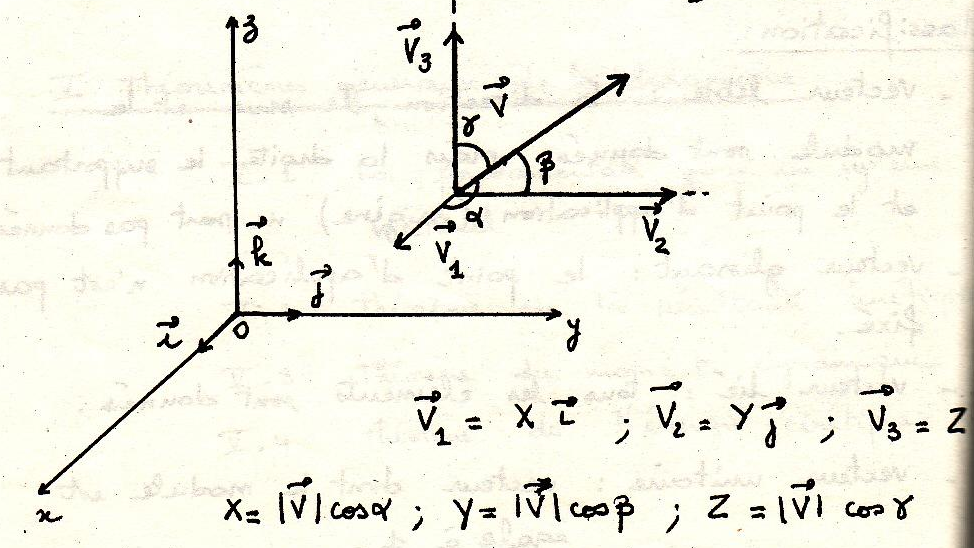
Аналитическое представление вектора:

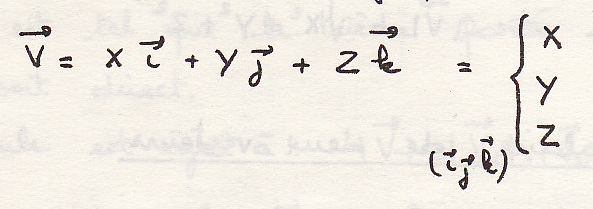
Всякий вектор в пространстве есть тензор 1-го рода (всякая совокупность трех величин)

Сложение векторов

Имеем несколько свободных векторов:

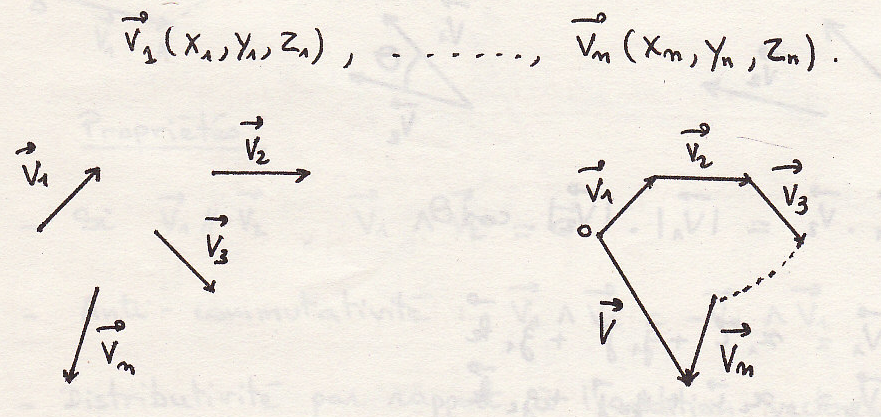
Сумма векторов – вектор, которой соединяет начало первого вектора с концом последнего:

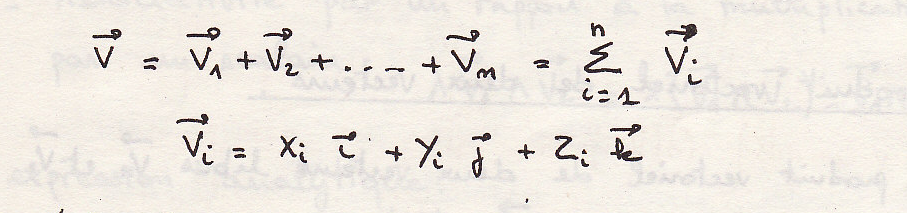
Если конец последнего вектора совпадает с началом первого, то многоугольник векторов называется замкнутым, в противном случае – разомкнутым.

Сумма двух векторов – третий вектор, изображаемый диагональю параллелограмма, построенного на слагаемых векторах.

Аналитическое выражение:

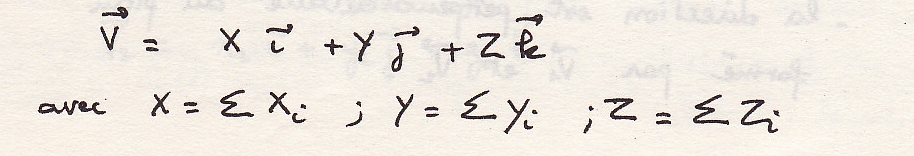
Модуль суммарного вектора:

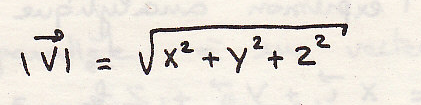
правило треугольника:

Правило паралеллограмма:

Свойства сложения векторов:

- коммунитативность

- ассоциативность

Вычитание векторов

Вычитание векторов – сложение уменьшаемого вектора с вектором противоположным вычитаемому

Скалярное произведение двух векторов

Скаляр (лат. scalaris- ступенчатый) – величина, характеризуемая только численным значением (положительное, отрицательное или ноль).

Произведение двух свободных векторов – произведение модулей на угол между векторами.

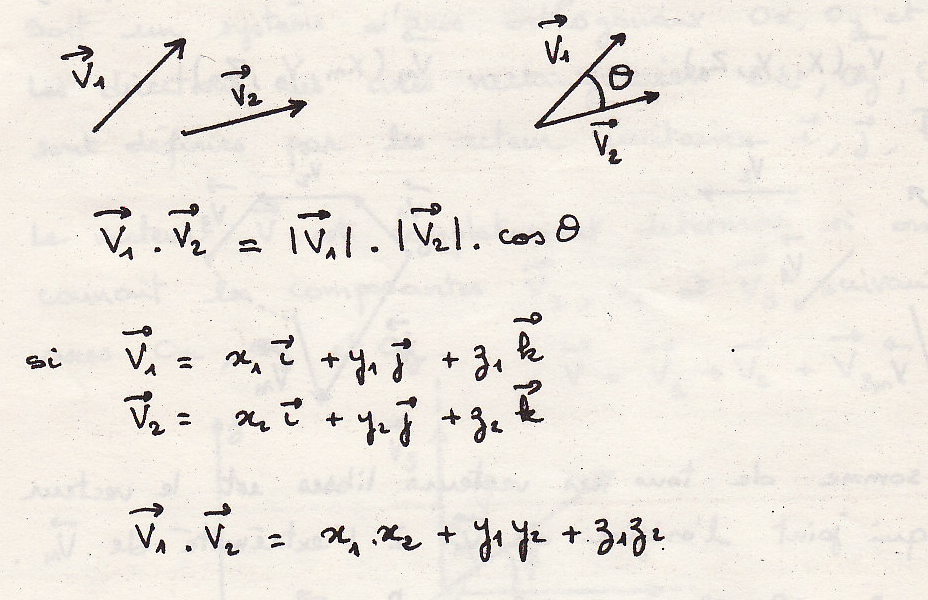
Скалярное произведение равно произведению модуля одного вектора и проекции другого вектора на направление первого

Скалярное произведение векторов обладает коммутативностью и дистрибутивностью

Векторное умножение двух векторов

Векторное умножение двух векторов – третий вектор:

- перпендикулярный к плоскости, на которой расположены два вектора

- направленный таким образом, что вектора образуют правую тройку, т.е. если смотреть с конца вектора, то поворот от первого множителя ко второму совершается против часовой стрелки.

-модуль равен:

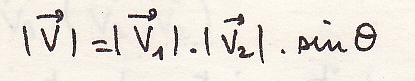
обозначается:

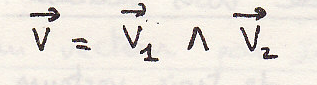
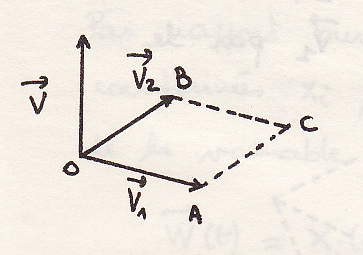
Равно по величине площади параллелограмма, построенного на этих векторах

- площадь параллелограмма ОАВС

Свойства:

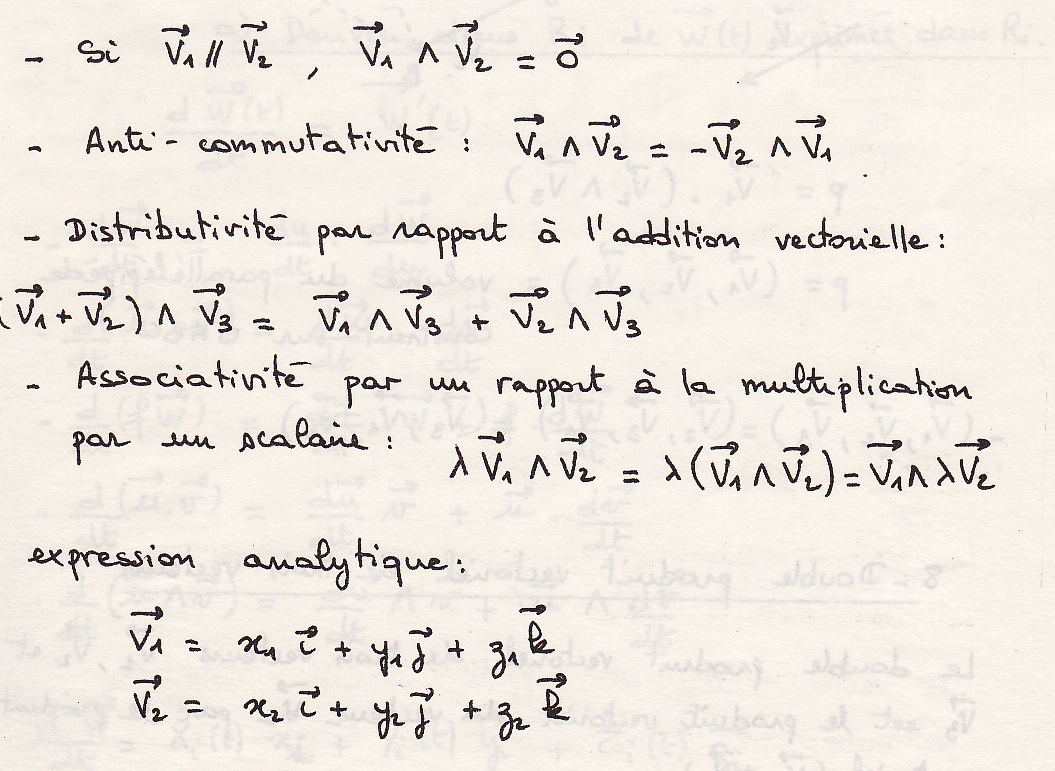
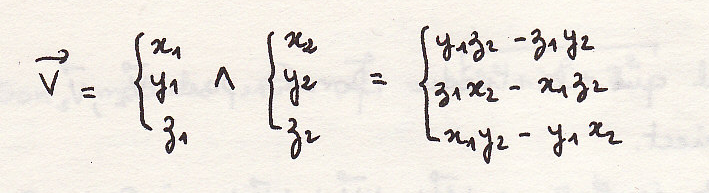
Смешанное произведение трех векторов

Смешанное или векторно-скалярное произведение трех векторов равно по абсолютному значению объему параллелепипеда, построенного на векторах как на ребрах.

В этом произведении вектор сначала умножается векторно на , а затем полученный вектор умножается скалярно на . В результате должен получится скаляр. Произведение будет положительным, если тройка векторов является правой, и отрицательной, если тройка векторов является левой.

Свойства:

- не изменяется от перестановки действий

- не изменяется от круговой перестановки сомножителей

- от перестановки метами двух сомножителей смешенное произведение меняет знак на противоположный

- если два вектора колленеарны, то смешанное произведение равно 0

Двойное векторное произведение трех векторов

Результат двойного векторного произведения - вектор

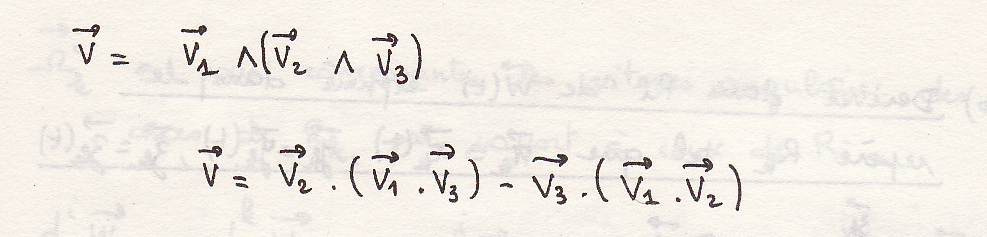
Двойное векторное произведение равно среднему вектору умноженному на скалярное произведение двух крайних, минус другой вектор скобки, умноженный на скалярное произведение оставшихся векторов.

Производная вектора в неподвижной системе координат

Рассмотрим вектор, который изменяется со временем по известному закону.

Проекции этого вектора на координатные оси представляют собой заданные функции времени.

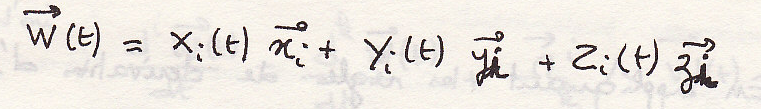
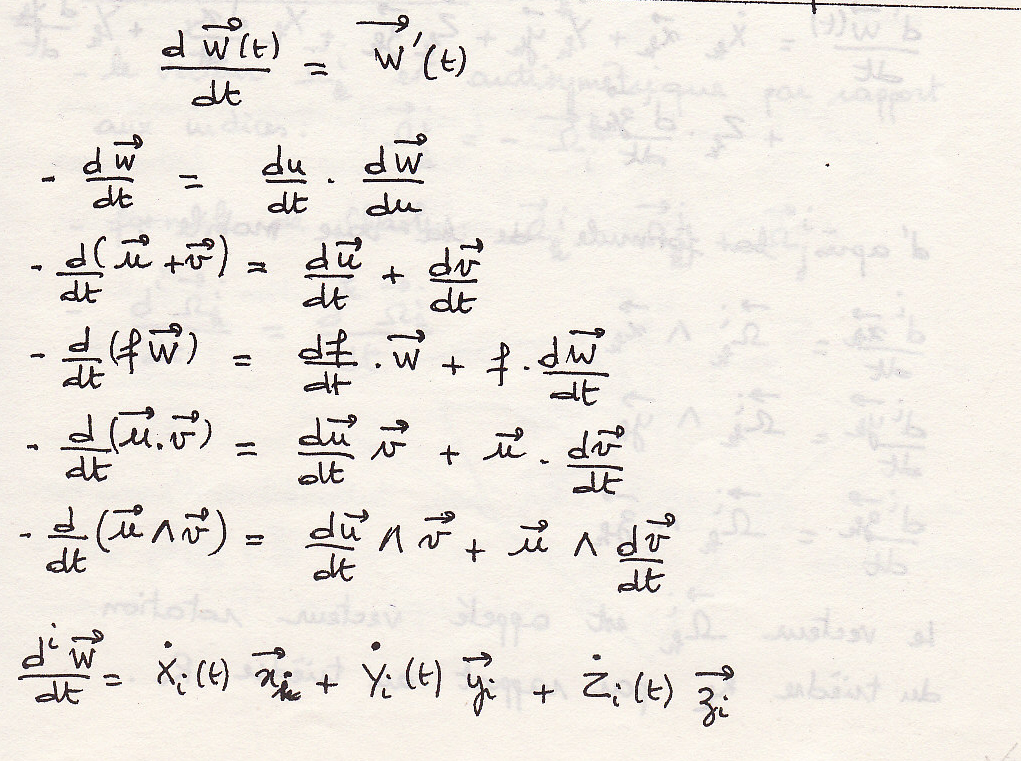
Производная вектора в подвижной системе координат

применяя правило производной вектора

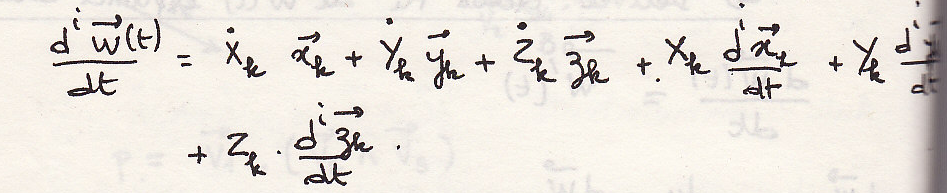
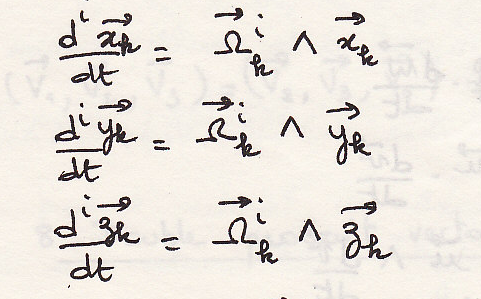
вектор вращения подвижной системы координат относительно неподвижной системы

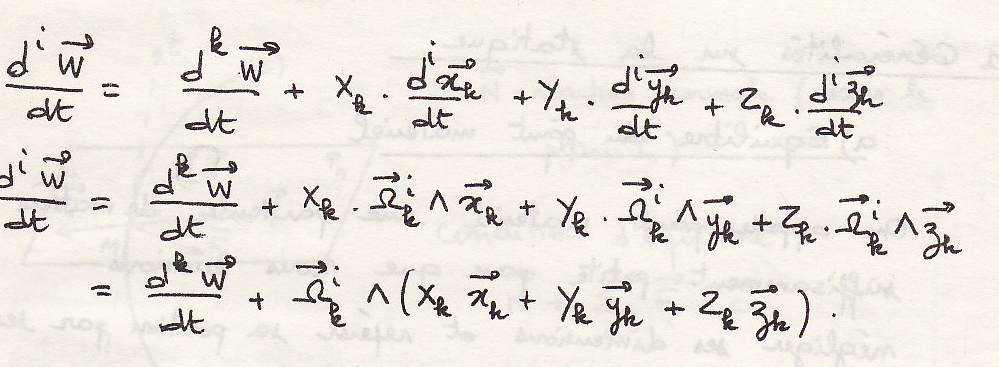
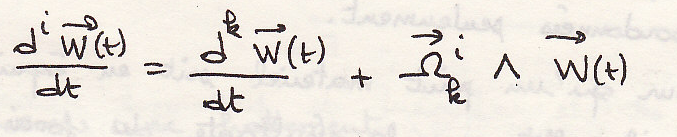
Свойства вектора

-