2. Измерение тесноты и силы корреляционной связи с использованием коэффициента детерминации и эмпирического корреляционного отношения

Для измерения тесноты и силы связи между факторным и результативным признаками рассчитывают специальные показатели – эмпирический коэффициент детерминации и эмпирическое корреляционное отношение .

Эмпирический коэффициент детерминации оценивает силу связи, определяя, насколько вариация результативного признака Y объясняется вариацией фактора Х (остальная часть вариации Y объясняется вариацией прочих факторов). Показатель рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формуле

, (9)

где – общая дисперсия признака Y,

– межгрупповая (факторная) дисперсия признака Y.

Значения показателя изменяются в пределах . При отсутствии корреляционной связи между признаками Х и Y имеет место равенство =0, а при наличии функциональной связи между ними - равенство =1.

Общая дисперсия характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных). Этот показатель вычисляется по формуле:

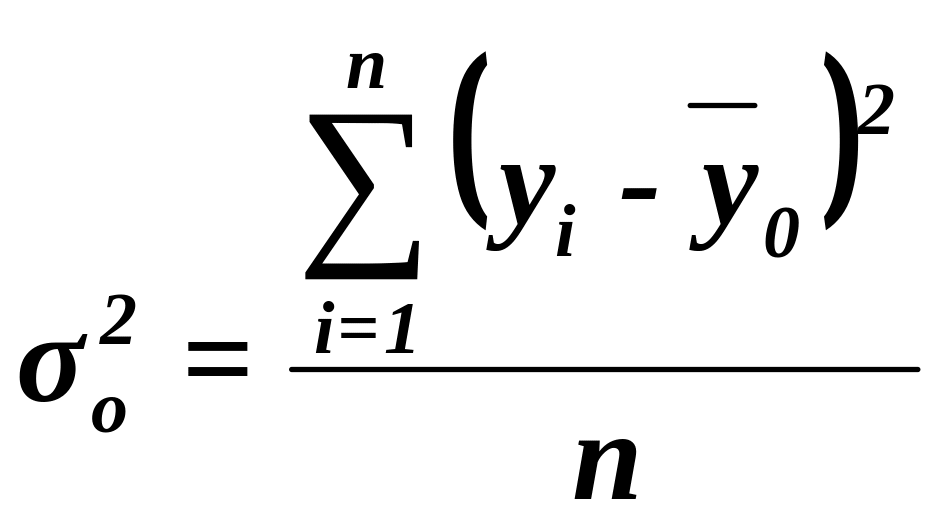, (10)

где y_i – индивидуальные значения результативного признака;

– общая средняя значений результативного признака;

n – число единиц совокупности.

Общая средняя вычисляется как средняя арифметическая простая по всем единицам совокупности:

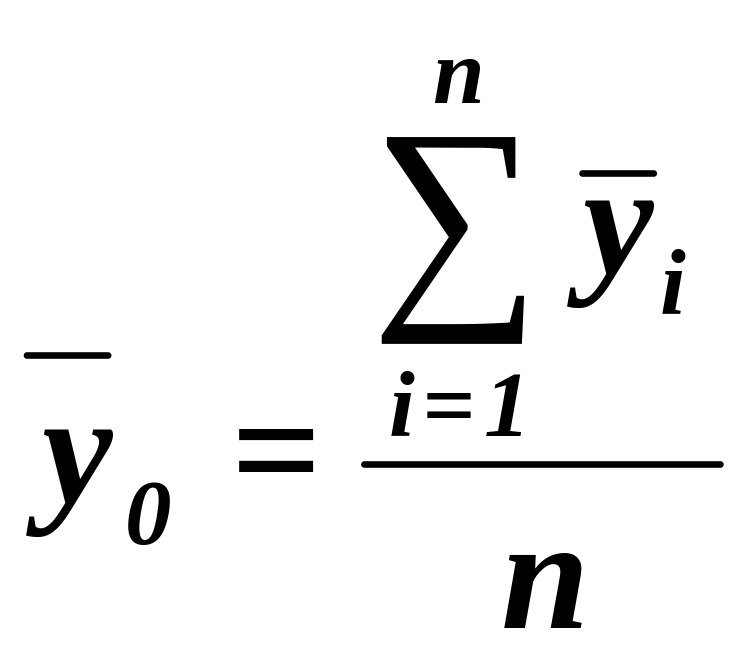(11)

или как средняя взвешенная по частоте групп интервального ряда:

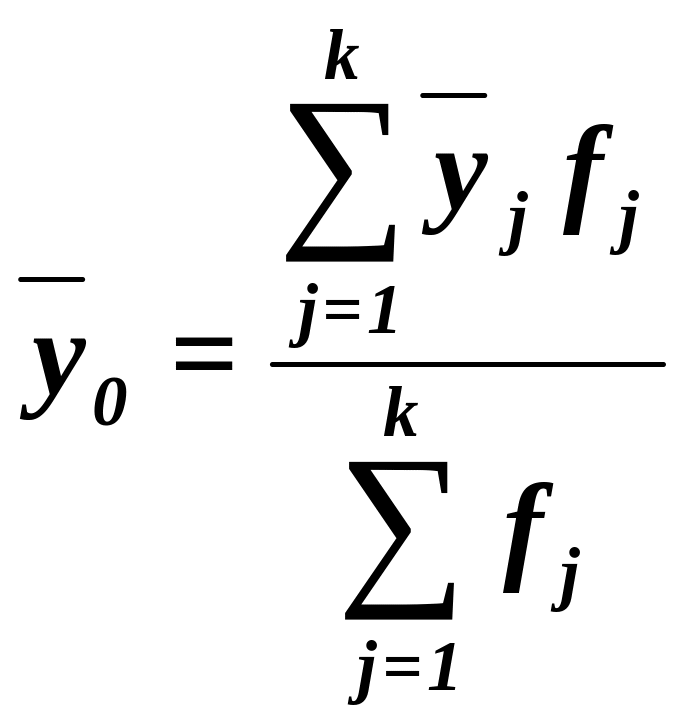(12)

Для вычисления удобно использовать формулу (11), т.к. в табл. 8 (графы 3 и 4 итоговой строки) имеются значения числителя и знаменателя формулы.

Расчет по формуле (11):

Для расчета общей дисперсии применяется вспомогательная таблица 12.

Таблица 12

Вспомогательная таблица для расчета общей дисперсии

Номер магазина п/п	Прибыль, млн. руб.
1	2	3	4	5
1	247,05	-62,70	3931,29	61033,70
2	448,81	139,06	19337,6836	201430,42
3	252,38	-57,37	3291,3169	63695,66
4	269,76	-39,99	1599,2001	72770,46
5	331,62	21,87	478,2969	109971,82
6	351,33	41,58	1728,8964	123432,77
7	184,49	-125,26	15690,0676	34036,56
8	381,48	71,73	5145,1929	145526,99
9	171,48	-138,27	19118,5929	29405,39
10	271,14	-38,61	1490,7321	73516,89
11	243,52	-66,23	4386,4129	59301,99
12	314,90	5,15	26,5225	99162,01
13	410,13	100,38	10076,1444	168206,61
14	261,81	-47,94	2298,2436	68544,48
15	187,48	-122,27	14949,9529	35148,75
16	292,38	-17,37	301,7169	85486,06
17	457,10	147,35	21712,0225	208940,41
18	308,76	-0,99	0,9801	95332,74
19	457,24	147,49	21753,3001	209068,42
20	398,67	88,92	7906,7664	158937,77
21	244,24	-65,51	4291,5601	59653,18
22	216,48	-93,27	8699,2929	46863,59
23	296,24	-13,51	182,5201	87758,14
24	299,33	-10,42	108,5764	89598,45
25	315,12	5,37	28,8369	99300,61
26	320,19	10,44	108,9936	102521,64
27	305,67	-4,08	16,6464	93434,15
28	326,33	16,58	274,8964	106491,27
29	342,67	32,92	1083,7264	117422,73
30	384,70	74,95	5617,5025	147994,09
Итого	9292,50	1807,583	175635,8834	3053987,75

Расчет общей дисперсии по формуле (10):

Общая дисперсия может быть также рассчитана по формуле

,

где – средняя из квадратов значений результативного признака,

– квадрат средней величины значений результативного признака.

Для демонстрационного примера

Тогда

Межгрупповая дисперсия измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка). Воздействие фактора Х на результативный признак Y проявляется в отклонении групповых средних от общей средней . Показатель вычисляется по формуле

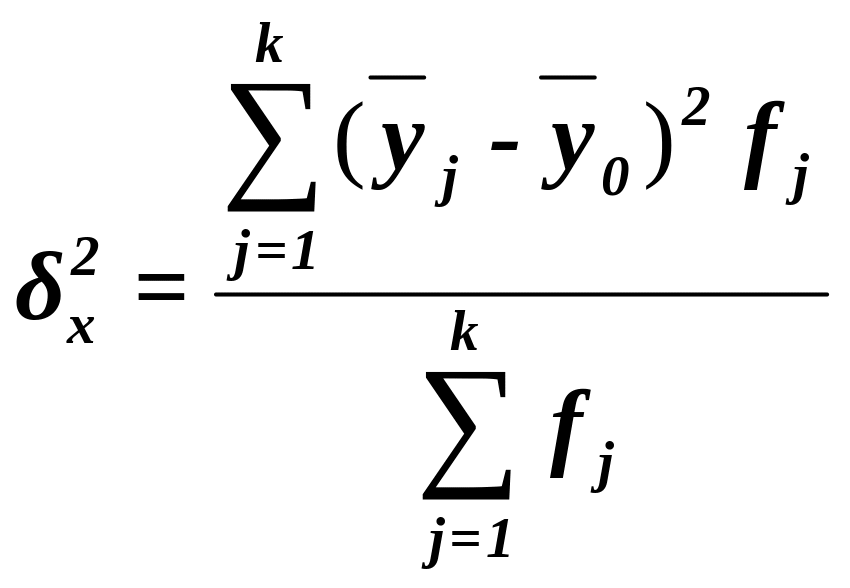
(13)

где –групповые средние,

– общая средняя,

–число единиц в j-ой группе,

k – число групп.

Для расчета межгрупповой дисперсии строится вспомогательная таблица 13, при этом используются групповые средние значения из табл. 8 (графа 5).

Таблица 13

Вспомогательная таблица для расчета межгрупповой дисперсии

Группы магазинов по выручке от продаж, млн руб.	Число магазинов,	Среднее значение в группе
1	2	3	4	5
462,57 - 510,19	3	181,15	- 128,6	49613,88
510,19 - 557,81	10	259,5	-50,25	25250,625
557,81 - 605,43	8	315,24	5,49	241,1208
605,43 - 653,05	5	371,77	62,02	19232,402
653,05 - 700,67	4	443,32	133,57	71363,776
Итого:	30			165701,8

Расчет межгрупповой дисперсии по формуле (11):

Расчет эмпирического коэффициента детерминации по формуле (9):

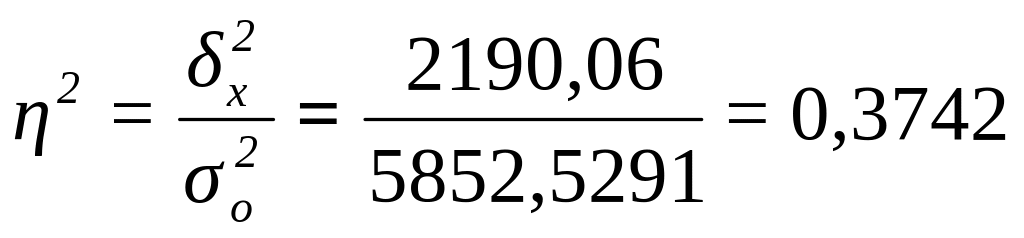^{или 37,4%}

Вывод. 37,4% вариации суммы прибыли магазинов обусловлено вариацией цен товара.

Эмпирическое корреляционное отношение оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле

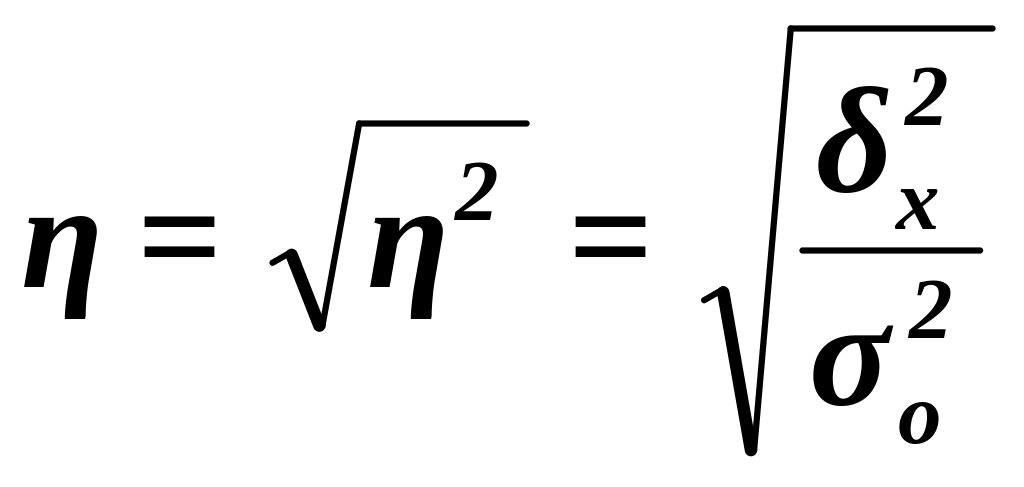(14)

Значение показателя изменяются в пределах . Чем ближе значение к 1, тем теснее связь между признаками. Для качественной оценки тесноты связи на основе служит шкала Чэддока (табл. 14):

Таблица 14

Шкала Чэддока

	0,1 – 0,3	0,3 – 0,5	0,5 – 0,7	0,7 – 0,9	0,9 – 0,99
Характеристика силы связи	Слабая	Умеренная	Заметная	Тесная	Весьма тесная

Расчет эмпирического корреляционного отношения по формуле (14):

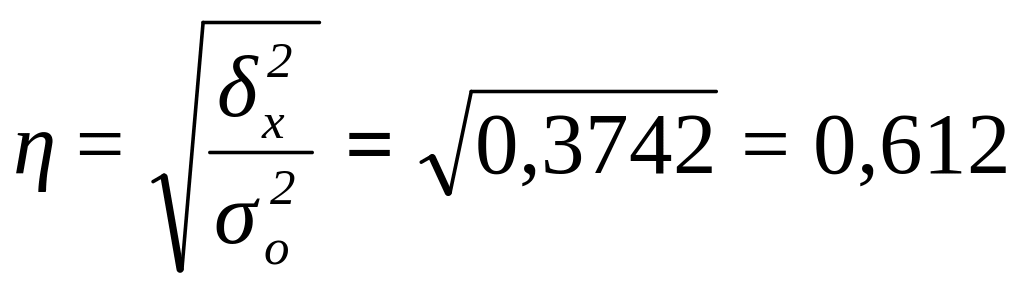
Вывод. Согласно шкале Чэддока связь между ценой товара и суммой выручки от продаж магазинов является тесной.