Теорема о ранге матрицы.

Ранг матрицы  A равен максимальному числу линейно независимых столбцов (или равен рангу системы столбцов матрицы А).

14. Транспортная задача с открытой моделью. Принцип построения модели и особенности её решения).

Транспортная задача, в которой суммарные запасы  и суммарные потребности  совпадают, называется закрытоймоделью; в противном случае - открытой. Открытая модель решается приведением к закрытой.

В случае, когда суммарные запасы превышают суммарные

потребности, т.е. 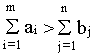 вводится фиктивный n+1 потребитель, потребности которого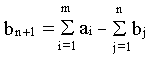 В случае, когда суммарные потребности превышают суммарные запасы, т.е. 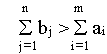 , вводится фиктивный m+1 поставщик, запасы которого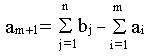 

Стоимость перевозки единицы груза, как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика полагают равными нулю, так как груз в обоих случаях не перевозится.

Прежде чем решать транспортную задачу, необходимо проверить, к какой модели она принадлежит, и если необходимо, то привести ее к закрытой модели.

15. Графы (понятие, определение, орграф, мультиграф, связный граф, дерево). Матричный способ задания графов.

Граф – это пара множеств G=(V;E), где V - непустое конечное множество, состоящее из p элементов – вершин графа G; E - множество неупорядоченных пар элементов q – рёбер графа G. G=(p;q).

Отрезки, соединяющие вершины – дуги, если указано, какая вершина является начальной.; рёбра, если ориентация не указана.

Граф, состоящий из дуг, - ориентированный (орграфом). Граф, образованный рёбрами – неориентированный.

Если между 2мя вершинами разрешено рисовать 2 или более ребра, граф называется мультиграфом. Если имеются вершины V1 и V2 и ребро e, образованное этими вершинами (e = (V1;V2) ϵ Е), то говорят, что ребро е инцидентно вершинам V1 и V2. Вершины V1 и V2 называются смежными.

Степень вершины – число рёбер, инцидентных данной вершине (это количество выходящих из неё рёбер). Вершина, степень которой равна 1, – висящая. Вершина, степень которой равна 2 и более, – ветвящаяся. Вершина, степень которой равна 0, – изолированная.

Последовательность рёбер (V0,V1), (V1,V2) … (Vk-1,Vk) – маршрут. Если в маршруте не повторяются рёбра, то такой маршрут называется цепью. Если V0 = Vk, то такая последовательность называется циклом. Если в цепи не повторяются вершины, то такая цепь – простая.

Граф – связный, если любая пара его вершин соединена маршрутом. Если в связном графе существует цикл, проходящий через все рёбра графа, то граф называется Эйлеровым. Связный граф, не имеющий циклов, - дерево.

Способы задания графов:

Матрица смежности вершин орграфа – это квадратная матрица n-го порядка, где n – число вершин. Строки и столбцы матрицы соответствуют вершинам графа. Элементы p_ij матрицы равны числу дуг, направленных от i-й вершины в j-ю. Если орграф состоит из однократных дуг, то элементы матрицы равны 0 или 1.В случае неориентированного графа ему вместе с ребром (x_i,x_j) принадлежит ребро (x_j,x_i).

Матрица смежности дуг орграфа – это квадратная матрица m-го порядка, где m – число дуг. Строки и столбцы матрицы соответствуют дугам графа. Элементы q_ij = 1, если дуга u_i непосредственно предшествует дуге u_j, и = 0 в остальных случаях.

Матрица смежности рёбер – это квадратная матрица m-го порядка, где m – число рёбер. Элементы q_ij = 1, если рёбра u_i и u_j имеют общую вершину, и = 0 в остальных случаях.

Матрица инцидентности – это прямоугольная матрица размерности m на n. Где строки соответствую вершинам, а столбцы – дугам графа. Элементы r_ij = 1, если дуга u_jj исходит из i-й вершины, = -1, если дуга заходит в i-ю вершину, = 0, если дуга не инцидента i-й вершине. В случае неориентированного графа, r_ij = 1 или 0.