Вторая теорема двойственности или теоремао дополняющей нежесткости.

Для того чтобы планы х* и у* пары двойственных задач были опти­мальными, необходимо и достаточно выполнение условий:

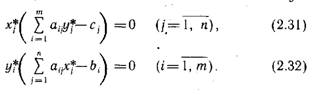
Условия (2.31), (2.32) называются условиями допол­няющей нежесткости. Из них следует:

         если какое-либо ограничение одной из задач ее оптимальным планом обра­щается в строгое неравенство, то соответствующая компо­нента оптимального плана двойственной задачи должна равняться нулю;

         если же какая-либо компонента опти­мального плана одной из задач положительна, то соответ­ствующее ограничение в двойственной задаче ее опти­мальным планом должно обращаться в строгое равенство.

Соответствие между переменными прямой и двойственной задач

Компоненты оптимального плана двойственной задачи находятся в строке целевой функции последней симплексной таблицы решенной задачи. Чтобы правильно выписать компоненты оптимального плана двойственной задачи необходимо учесть соответствие между переменными двойственных задач, устанавливаемое для канонических форм, в котором базисным переменным одной задачи отвечают свободные переменные другой и наоборот.

Экономическая интерпретация дополнительных переменных двойственной задачи

Основные переменные х_i обозначали количество произведенной продукции i-го вида, дополнительные переменные обозначали количество излишков соответствующего вида ресурсов, каждое из неравенств выражало собой расход определенного вида сырья в сравнении с запасом этого сырья.

12. Транспортная задача (тз). Постановка тз в матричной и математической форме, методы нахождения начального опорного плана.

 Постановка задачи

Транспортная задача (классическая) — задача об оптимальном плане перевозок однородного продукта из однородных пунктов наличия в однородные пункты потребления на однородных транспортных средствах (предопределённом количестве) со статичными данными и линеарном подходе (это основные условия задачи).

Для классической транспортной задачи выделяют два типа задач: критерий стоимости (достижение минимума затрат на перевозку) или расстояний и критерий времени (затрачивается минимум времени на перевозку).

Постановка ТЗ в математической форме

Математическая модель транспортной задачи имеет вид

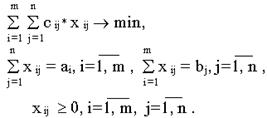
Постановка ТЗ в матричной форме

Классическая транспортная задача ЛП формулируется следующим образом. Имеется m пунктов производства (поставщиков) и n пунктов потребления (потребителей) однородного продукта. Заданы величины:

- объем производства (запас) i-го поставщика, i=1, m ;

- объем потребления (спрос) j-го потребителя, i=1, n ;

 - стоимость перевозки (транспортные затраты) единицы продукта от i-го поставщика к j-му потребителю.

Требуется составить такой план перевозок, при котором спрос всех потребителей был бы выполнен и при этом общая стоимость всех перевозок была бы минимальна.

Методы нахождения начального опорного плана

Как и при решении задачи линейного программирования, симплексным методом, определение оптимального плана транспортной задачи начинают с нахождения какого-нибудь ее опорного плана.

Для определения опорного плана существует несколько методов:

Способ «северо-западного угла»:

Первой загружается клетка (1;1). Если закрывается строка, то следующей загружается клетка (2;1); если же закрывается столбец, то следующей загружается клетка (1;2). Итак, каждый раз загружается клетка, соседняя либо по строке, либо по столбцу (в зависимости от конкретных данных задачи). Последней будет загружена клетка (m;n). В результате загруженные клетки расположатся вдоль диагонали (1;1) – (m;n), поэтому способ «северо-западного угла» называют ещё диагональным способом.

Способ «минимального элемента»:

Первой в распределительной таблице загружается клетка с наименьшим тарифом. Далее загружается клетка той же строки (столбца) со следующим по величине тарифом и т.д.

Поскольку при заполнении таблицы увеличиваются величины тарифов, то, как правило, построенный план оказывается ближе к оптимальному, нежели построенный способом «северо-западного угла».

Способ Фогеля:

Прежде всего по каждой строке и каждому столбцу находят разности двух наименьших тарифов (будем записывать их за пределами распределительной таблицы напротив соответствующих строк и столбцов). Из этих разностей выделяется наибольшая, и в соответствующей строке (столбце) загружается клетка с наименьшим тарифом. Закрывшаяся строка (столбец) исключается из дальнейшего рассмотрению. Описанная операция повторяется до тех пор, пока не закроются все строки и столбцы, т.е. m + n - 1 раз.

13. Транспортная задача (методы нахождения оптимального плана ТЗ, теорема о ранге матрицы).

Методы нахождения оптимального плана

Методы решения транспортной задачи сводятся к простым операциям с транспортной таблицей, которая имеет вид:

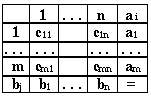
Базисными клетками транспортной таблицы являются клетки с отличными от нуля положительными перевозками, остальные клетки - свободные. Базисные клетки образуют опорный план транспортной задачи, если выполняются два условия:

1) сумма перевозок в каждой строке равна запасу  в данной строке;

2) сумма перевозок в каждом столбце равна соответствующему столбцу спроса

Вырожденный и не вырожденный план.

Опорный план транспортной задачи содержит не более r=n+m-1 отличных от нуля перевозок 

Опорный план называется вырожденным, если число ненулевых перевозок  меньше r=n+m-1 (теорема о ранге матрицы), опорный план - не вырожден, если число ненулевых перевозок равно r=n+m-1.

Метод потенциалов является модификацией симплекс-метода решения задачи линейного программирования применительно к транспортной задаче. Он позволяет, отправляясь от некоторого допустимого решения, получить оптимальное решение за конечное число итераций. Общая схема отдельной итерации такова. По допустимому решению каждому пункту задачи сопоставляется число, называемое его предварительным потенциалом. Пунктам Аi соответствуют числа ui, пунктам Bj - числа vj. Они выбираются таким образом, чтобы их разность на k-й итерации была равна Сij - стоимости перевозки единицы продукции между пунктами Аi и Вj:

vj[k] – ui[k] Cij, i=1, ..., m; j=1, …, n.

Если разность предварительных потенциалов для каждой пары пунктов Аi, Вj не превосходит Сij, то полученный план перевозок является решением задачи. В противном случае указывается способ получения нового допустимого плана, связанного с меньшими транспортными издержками. За конечное число итераций находится оптимальный план задачи.