7. Симплексный метод (назначение метода, приведение систем к предпочтительному виду (3 случая), построение начального опорного плана).

Назначение метода

В общем виде, когда в задаче участвуют N-неизвестных, можно сказать, что область допустимых решений, задаваемая системой ограничивающих условий, представляется выпуклым многогранником в n-мерном пространстве и оптимальное значение целевой функции достигается в одной или нескольких вершинах. Решить данные задачи графически, когда количество переменных более 3 весьма затруднительно. Существует универсальный способ решения задач линейного программирования, называемый симплекс-методом.

Идея симплекс-метода заключается в следующем. Сначала нужно найти некоторую (начальную) вершину многогранника допустимых решений (начальное допустимое базисное решение). Затем нужно проверить это решение на оптимальность. Если оно оптимально, то решение найдено; если нет, то перейти к другой вершине многогранника и вновь проверить на оптимальность. Ввиду конечности вершин многогранника (следствие конечности ограничений задачи ЛП) за конечное число "шагов" мы найдем искомую точку минимума или максимума. Надо заметить, что при переходе от одной вершины к другой значение целевой функции убывает (в задаче на минимум) или возрастает (в задаче на максимум).

Приведение к предпочтительному виду (3 случая). Построение начального опорного плана (x0)

1. Пусть в системе ограничений имеется единичный неотрицательный базис (переменная, которая имеет коэффициент = 1 и не повторяется в других ограничениях):

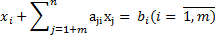
Говорят, что ограничение канонической ЗЛП имеет предпочтительный вид, если при неотрицательности его правой части (b_i >= 0), левая часть содержит переменную, входящую с коэффициентом = 1, а в остальных ограничениях с коэффициентом = 0. Если каждое ограничение канонической ЗЛП имеет предпочтительный вид, то начальный опорный план строится следующим образом:

• Предпочтительные переменные выбираются в качестве базисных, а все остальные свободные.

• Свободные переменные приравниваются к 0, а базисные переменные – к свободным членам.

2. Пусть система ограничений имеет вид: . Сведём задачу к каноническому виду, добавив к левым частям системы ограничений дополнительные переменные x_n+I >= 0. Соответственно получим систему ограничений: . В целевую функцию дополнительные переменные вводятся с коэффициентом = 0 (C_n+I = 0).

Пример: maxZ  = x1 + 2x2 + 3x3 + 4x4 + 5x5 -M w1 – 0*x6 - Mw2 – x7*0 – Mw3

X 2 + x3 – 2x4 + 7x5 =2; +w1

X1 + x3 – 2x4 – 6x5 >= 12;  -x6 + w2

X1 + x2 - 2x4 + 7x5 >= 7;     -x7 +w3

X₀ = 0,0,0,0,0,0,0,2,12,7Z(x₀)= -21M

8. Симплексный метод (назначение метода, симплексные таблицы, правила построения симплекс-таблиц, понятие индексной строки, разрешающего элемента, правило прямоугольника).

Назначение метода

Симплекс-метод - это итеративный процесс направленного решения системы уравнений по шагам, который начинается с опорного решения и в поисках лучшего варианта движется по угловым точкам области допустимого решения, улучшающих значение целевой функции до тех пор, пока целевая функция не достигнет оптимального значения. Приведя модель задачи к предпочтительному виду её заносят в симплексную таблицу.

Рабочая часть таблицы, начиная с 3 столбца и 3 строки, содержит элементы расширенной матрицы, над которыми будут производится преобразования с целью получения оптимального плана. В столбец БП занесены базисные (предпочтительные) переменные. Столбец Сб содержит коэффициенты целевой функции, стоящие при базисных переменных. Столбец А₀ содержит свободные члены (b_i >= 0) системы ограничений. Сверху, над рабочей частью таблицы, указаны все переменные и коэффициенты целевой функции C_j. Последняя строка таблицы – индексная (строка оценок).

Если задача решается на максимум среди отрицательных оценок находят максимальную по абсолютной величине, если на минимум – из положительных выбирается максимальное значение, столбец j0, определённый этой оценкой – разрешающий. Строка i0, соответствующая минимальному симплексному отношению (b_i\a_ij0 > 0), – разрешающая. На пересечении разрешающего столбца и разрешающей строки находится разрешающий элемент.

Правило прямоугольника

Чтобы найти элемент новой симплексной таблицы, нужно воспользоваться правилом прямоугольника. Для этого в исходной таблице выделяют прямоугольник, вершинами которого служат нужные для вычисления элементы. Элемент новой таблицы = (произведение главной диагонали – произведение побочной диагонали) \ разрешающий элемент.