Определение модели. Моделирование как метод исследования систем. Этапы моделирования.
Модель – это упрощённое представление о реальном объекте, процессе или явлении. Модель воспроизводит в специально оговорённом виде строение и свойства исследуемого объекта.
Моделирование – это метод познания, состоящий в создании и исследовании моделей.
Системный подход – это подход, который связывается с исследованиями, проводимыми многоаспектно, комплексно, с разных сторон изучая предмет или явление.
Системный анализ – это деятельность человека, на основе которой обеспечивается представление исследуемого объекта в виде системы. Система сохраняет свою целостность до тех пор, пока она сохраняет неизменной свою структуру (множество связей между элементами). Если структура системы меняется, то система может перестать функционировать, как целое.
Этапы моделирования:
1. Постановка задачи. Определяется цель анализа, вырабатывается подход к исследованию проблемы.
2. Изучение теоретических основ и сбор информации об объекте оригинала. Подбирается или разрабатывается подходящая теория, если ее нет, устанавливаются причинно-следственные связи между переменными, описанными объектами, определяются входящие и выходящие данные, принимаются упрощенные предложения.
3. Формализация. Выбор системы условных обозначений, устанавливается класс задачи, к которой может быть отнесена полученная математическая модель.
4. Выбор метода решения. Устанавливаются окончательные параметры модели для получения математической задачи, выбирается который либо метод решения или разрабатывается специальный.
5. Реализация модели. Пишется программа, отлаживается, тестируется и получается решение задачи.
6. Анализ полученной информации. Сопоставляются полученное решение и предполагаемое.
7. Проверка адекватности реальному объекту. Результаты сопоставляются либо с имеющейся в объекте информацией, либо проводится эксперимент и его результаты сопоставляются с расчетными.
Классификация видов моделирования(4 классификации) и их характеристики.
1. По области использования:
Учебные модели – используются при обучении;
Опытные – это уменьшенные или увеличенные копии проектируемого объекта. Используют для исследования и прогнозирования его будущих характеристик
Научно-технические - создаются для исследования процессов и явлений
Игровые – репетиция поведения объекта в различных условиях
Имитационные – отражение реальности в той или иной степени (это метод проб и ошибок)
2. По фактору времени:
Динамическая модель – это модель, когда состояние системы изменяется во времени, т.е. происходят процессы изменения и развития системы.
Статическая модель – это модель, которая описывает состояние системы в определённый момент времени.
3. По отрасли знаний - математические, биологические, химические, социальные, экономические, исторические и т. д.
4) По форме представления:
Материальные – это предметные (физические) модели. Они всегда имеют реальное воплощение. Отражают внешнее свойство и внутреннее устройство исходных объектов, суть процессов и явлений объекта-оригинала. Это экспериментальный метод познания окружающей среды. Примеры: детские игрушки, скелет человека, чучело, макет солнечной системы, школьные пособия, физические и химические опыты
Абстрактные (нематериальные) – не имеют реального воплощения. Их основу составляет информация, это теоретический метод познания окружающей среды.
Математическое моделирование, его классификация, характеристика.
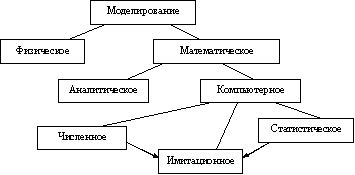
Физическое – используется сама система, либо подобная ей (летательный аппарат в аэродинамической трубе).
Математическое – процесс установления соответствия реальной системе S математической модели M и исследование этой модели, позволяющее получить характеристики реальной системы.
Аналитическое – процессы функционирования элементов записываются в виде математических соотношений (алгебраических, интегральных, дифференциальных, логических и т.д.). Аналитическая модель может быть исследована методами:
а) аналитическим (устанавливаются явные зависимости, получаются, в основном, аналитические решения);
б) численным (получаются приближенные решения);
в) качественным (в явном виде можно найти некоторые свойства решения).
Компьютерное – математическое моделирование формулируется в виде алгоритма (программы для ЭВМ), что позволяет проводить над ней вычислительные эксперименты.
Численное – используются методы вычислительной математики (отличается от численного аналитического тем, что возможно задание различных параметров модели).
Статистическое – обработка данных о системе (модели) с целью получения статистических характеристик системы.
Имитационное – воспроизведение на ЭВМ (имитация) процесса функционирования исследуемой системы, соблюдая логическую и временную последовательность протекания процессов, что позволяет узнать данные о состоянии системы или отдельных ее элементов в определенные моменты времени.
Этапы моделирования.