
- •Санкт-Петербург
- •Содержание
- •Введение
- •Аннотация
- •1. Значение, общие принципы и методы технического анализа Основные понятия: технический контроль производств, технический анализ
- •Технический анализ – важнейшая составная часть технического контроля производств
- •Классификация методов технического анализа
- •Аналитический процесс Пробоотбор и пробоподготовка
- •Измерение и оценка результата Чувствительность аналитической методики
- •Случайная и систематическая погрешности
- •2. Гравиметрический (весовой анализ) Сущность гравиметрического анализа, его возможности и точность. Практическое значение метода
- •Разновидности гравиметрического анализа Форма осаждения и весовая форма
- •Требования, предъявляемые к форме осаждения и весовой форме
- •Контроль полноты осаждения
- •Образование осадков, их свойства, зависимость характера осадков от условий осаждения
- •Гравиметрическая форма.
- •Выбор осадителя; органические осадители.
- •Расчеты в гравиметрическом анализе; соотношение эквивалентности, аналитический фактор
- •Основные методы титриметрического анализа. Основные приемы титрования
- •Метод кислотно-основного титрования (нейтрализации)
- •Индикаторы в методе кислотно-основного титрования
- •Кривые титрования
- •Окислительно-восстановительное титрование (оксидиметрия), его разновидности
- •Титрование по методу осаждения. Комплексометрическое титрование
- •Выражение концентрации рабочих растворов. Расчеты в титриметрии
- •Термометрическое титрование.
- •Кондуктометрия. Кондуктометрическое титрование
- •Вольтамперометрия. Прямая полярография. Амперометрическое титрование
- •Контрольные вопросы к главе 1.3.
- •1.4. Спектральные и оптические методы анализа
- •Оптические спектры
- •Величины светопоглощения
- •Спектр поглощения
- •Выбор длины волны и светофильтра
- •Чувствительность фотоколориметрических и спектрофотометрических методов
- •Основные приемы фотометрического анализа
- •Приборы фотометрического анализа Для количественной оценки интенсивности окраски или светопоглощения применяют различные приборы:
- •Электронные спектры поглощения органических соединений
- •Типы электронных переходов
- •Инфракрасная спектроскопия
- •Устройство ик - спектрометра
- •Ядерный магнитный резонанс
- •Химический сдвиг
- •Спин-спиновое взаимодействие
- •Контрольные вопросы к теме 1.4
- •1.5. Хроматографический анализ и хромато-масс-спектрометрия хроматографические методы анализа
- •Области применения хроматографии
- •Молекулярная адсорбционная хроматография жидких веществ
- •Адсорбенты
- •Растворители
- •I. По механизму разделения
- •II. По форме проведения процесса
- •Газовая хроматография
- •Хромато-масс-спектрометрия
- •Контрольные вопросы к теме 1.5.
- •Заключение
- •Список литературы к разделу 1.1.-1.3.
- •Список литературы к разделу 1.4.-1.5.
- •Терминологический словарь к разделу 1
Измерение и оценка результата Чувствительность аналитической методики
Интенсивность аналитического сигнала - это численное значение свойства, связанное с содержанием анализируемого компонента. Так, например, масса высушенного осадка и объем израсходованного раствора определяют интенсивность аналитического сигнала в гравиметрическом и титриметрическом анализах соответственно.
Уравнение связи выражает зависимость между интенсивностью аналитического сигнала (измеряемой величиной) и содержанием анализируемого компонента:
P=f(c) (1)
где P – интенсивность аналитического сигнала; c – концентрация.
Вид функциональной зависимости определяется главным образом особенностями аналитического сигнала. Зависимость может быть линейной, логарифмической и т.д.
Пусть между величиной y, характеризующей количество определяемого вещества, и измеряемой величиной x существует зависимость
аналитическая функция у=f(х) (2)
или
градуировочная функция х=f(у) (3)
Данные зависимости можно получить путем градуировки. В простых случаях величины х и у прямо пропорциональны.
Чувствительность аналитической методики E – это величина, определяемая как первая производная градуировочной функции (3):
Е= f,(у)=dx/dy (4)
Случайная и систематическая погрешности
Как небрежное или неправильное выполнение операций анализа, так и погрешность в расчете ведут к неверному результату.
Погрешность измерения - это отклонение результата измерения от истинного значения измеряемой величины.
Δxi=xi - µ (5)
где Δxi - абсолютная погрешность измерения; xi – результат анализа; µ - истинное содержание анализируемого компонента в пробе.
Отношение абсолютной погрешности измерения к истинному значению измеряемой величины называется относительной погрешностью измерения.
![]() (6)
(6)
Погрешность измерения зависит от многих факторов: от класса точности применяемых приборов, методики измерения, индивидуальных особенностей наблюдателя и т.д.
Погрешность измерения, которая при повторных измерениях остаётся постоянной или закономерно изменяется, называется систематической погрешностью.
Знак данной систематической погрешности от опыта к опыту не меняется. Систематическая погрешность или только занижает, или только завышает результат.
Источники систематических погрешностей довольно многочисленны. Наибольшее значение из них имеют погрешности, обусловленные применяемыми приборами и реактивами, погрешности метода и погрешности, связанные с индивидуальными особенностями аналитика и т.д.
Погрешность, которая при повторных измерениях изменяется случайным образом, называется случайной погрешностью измерения.
Знак случайной величины в серии измерений не остаётся постоянным и от опыта к опыту меняется.
Грубые погрешности, существенно превышающие ожидаемые при данных условиях, называются промахами.
Они обычно бывают следствием грубых оперативных погрешностей аналитика (потеря раствора с осадком при фильтровании, потеря осадка при прокаливании или взвешивании и т.д.).
Правильность измерений называют качество измерений, отражающее близость к нулю систематических погрешностей.
Сходимостью измерений называют качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в одинаковых условиях.
Истинное значение физической величины определяется как такое значение, которое идеальным образом отражало бы в качественном и количественном отношениях соответствующее свойство объекта.
Обработка погрешностей. Стандартное отклонение
Методами статистического анализа можно по результатам случайной выборки найти наиболее вероятное значение содержания компонента в пробе.
Пусть x - численное значение единичного определения (варианта), x1,x2…xn - результаты параллельных определений (совокупность вариант). Сумму вариант, деленную на число вариант n, называют средним или средним арифметическим:
![]() (7)
(7)
Случайное отклонение (d) – это разность между отдельным результатом и средним значением:
![]() (8)
(8)
Выборочное стандартное отклонение отдельного определения S рассчитываю по формуле:
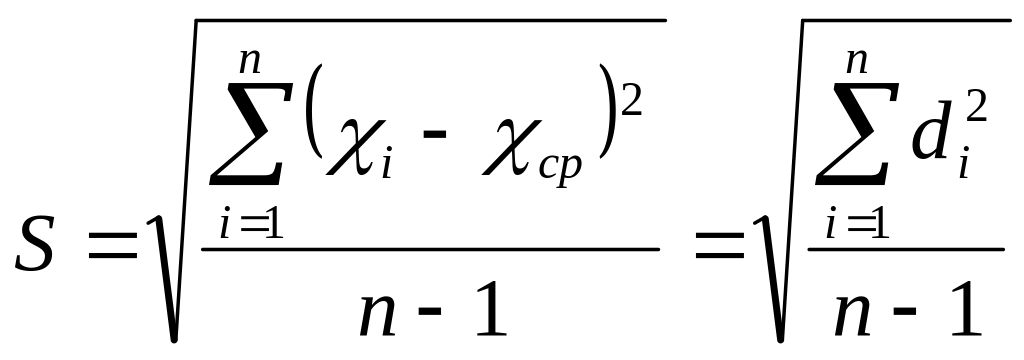 (9)
(9)
Квадрат стандартного отклонения называют дисперсией:
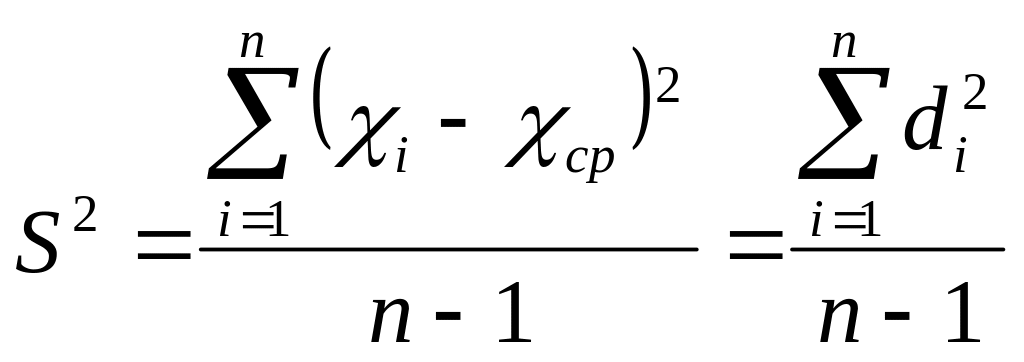 (10)
(10)
Для оценки воспроизводимости вычисляют выборочную дисперсию среднего значения:
 (11)
(11)
и стандартное отклонение среднего результата:
 (12)
(12)
